Лекция 4. Понятие обратной матрицы. Свойства обратной матрицы. Нахождение обратной матрицы. Вывод общей формулы для обратной матрицы.
Квадратная матрица называется обратной по отношению к данной квадратной матрице, если ее умножение как справа, так и слева на данную матрицу дает единичную матрицу. Для матрицы А обратная матрица обозначается  . По определению,
. По определению,  .
.
Квадратную матрицу называют особенной (или вырожденной), когда ее определитель равен нулю, и неособенной (или невырожденной), когда ее определитель отличен от нуля.
Теорема. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы определитель матрицы А был отличен от нуля, т.е. чтобы матрица А была неособенной (невырожденной).
Доказательство. Рассмотрим процесс обращения матрицы. Пусть А – неособенная квадратная матрица n-го порядка, определитель которой не равен нулю. Составим матрицу из алгебраических дополнений элементов данной матрицы и затем транспонируем ее. Полученная матрица называется союзной (или присоединенной) по отношению к матрице А и обозначается  :
:
 .
.
Вычисляя произведения 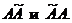 по правилам умножения матриц, получим
по правилам умножения матриц, получим 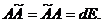
Докажем справедливость этих равенств на примере матрицы третьего порядка. Пусть  , тогда
, тогда 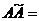
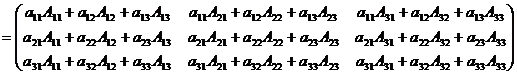
Согласно свойствам определителя все элементы произведения, кроме диагональных, равны нулю. Таким образом, 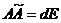 . Так как определитель матрицы А не равен нулю, то
. Так как определитель матрицы А не равен нулю, то 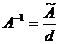 .
.
Пример 1. Найти обратную матрицу для матрицы  .
.
1. Вычисляем определитель данной матрицы
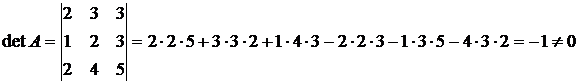 Т.к. определитель не равен нулю, то обратная матрица существует.
Т.к. определитель не равен нулю, то обратная матрица существует.
2. Находим алгебраические дополнения элементов матрицы А.

3. Составляем союзную (присоединенную)матрицу
 .
.
4. Вычисляем обратную матрицу 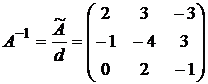 .
.
5. Проверка: 
Условия существования обратной матрицы.
1.  может существовать только тогда, когда А – квадратная матрица.
может существовать только тогда, когда А – квадратная матрица.
2.  существует только в том случае, когда определитель
существует только в том случае, когда определитель  .
.
Свойства обратной матрицы.
Если А есть квадратная невырожденная (т.е. её определитель не равен нулю) матрица, то обратная к ней матрица  обладает следующими свойствами:
обладает следующими свойствами:
1. Обратная матрица перестановочна с А. Оба произведения дают единичную матрицу  .
.
2. Обратная к А матрица является единственной.  , тогда и только тогда, когда
, тогда и только тогда, когда 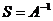 .
.
3. Определитель обратной к А матрицы равен обратной величине определителя матрицы А: 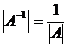 .
.
4. Обратная матрица является невырожденной.
5. Обратной матрицей к  будет матрица
будет матрица 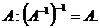
6. Матрица, обратная к транспонированной, равна транспонированной обратной матрице: 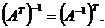
7. Если матрица симметрическая, то такой же будет обратная матрица.
8. Матрица, обратная к произведению матриц, равна произведению обратных матриц, взятых в обратном порядке при условии, что обратные матрицы существуют. Если существуют 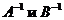 , то
, то 
Получение обратной матрицы с помощью ее расчленения на подматрицы.
Вычисление обратной матрицы часто может быть упрощено с помощью расчленения ее на четыре подматрицы, причем верхняя левая и нижняя правая подматрицы должны быть квадратными.  , где A и D – квадратные подматрицы. Процедура получения обратной матрицы
, где A и D – квадратные подматрицы. Процедура получения обратной матрицы  обусловлена тем фактом, что произведение этих матриц должно быть равно единичной матрице
обусловлена тем фактом, что произведение этих матриц должно быть равно единичной матрице 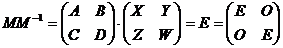 . Отсюда по правилу умножения матриц мы имеем:
. Отсюда по правилу умножения матриц мы имеем:

При условии, что A и D- невырожденные матрицы, из (3) следует  . Подставим в (1) получим
. Подставим в (1) получим  . Аналогично из (2) и (4):
. Аналогично из (2) и (4):  .
.
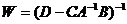 . В соответствии с этими формулами в процессе вычислений потребуется найти четыре обратных матрицы.
. В соответствии с этими формулами в процессе вычислений потребуется найти четыре обратных матрицы.
Если же использовать другое тождество:  , то мы получим более удобные для расчета выражения
, то мы получим более удобные для расчета выражения  , откуда
, откуда
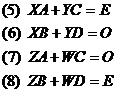
Из (6) следует  , а из (8)
, а из (8)  .
. 
Поскольку все восемь уравнений справедливы, то мы можем воспользоваться любыми четырьмя уравнениями, достаточными для нахождения неизвестных матриц.
Первый вариант. Воспользуемся двумя уравнениями из первой четверки – первым и третьим, и двумя уравнениями из второй четверки шестым и восьмым. Соответственно из (1) и (3) получаем выражения для X и Y:  ,
,  , а из (6) и (8) -
, а из (6) и (8) -  и
и  . При проведении расчетов по этим формулам необходимо определить только две обратные матрицы.
. При проведении расчетов по этим формулам необходимо определить только две обратные матрицы.
Порядок расчета следующий:



Второй вариант. Можно выбрать другую четверку уравнений (2),(4), (5) и (7). Из них мы получим следующие выражения  ,
, 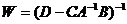 ,
,
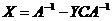 ,
,  . Приведем полный порядок расчета:
. Приведем полный порядок расчета:

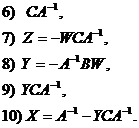
При этом невырожденной в первом случае должна быть матрица D, а во втором A.
Выбор процедуры расчета определяется свойствами матрицы М и ее подматриц. В каждом отдельном случае используются те свойства, которые могут в наибольшей степени упростить расчеты. Например, если  , то лучше пользоваться первым расчетом, т.к. в нем пользуются матрицами
, то лучше пользоваться первым расчетом, т.к. в нем пользуются матрицами  . Эти матрицы довольно легко найти поскольку D – диагональная матрица, а А имеет размеры 2х2.
. Эти матрицы довольно легко найти поскольку D – диагональная матрица, а А имеет размеры 2х2.
Пример 2. С помощью разбиения на клетки обратить матрицу

Обозначим

1) 
2) 
3) 
4) 
5) 
6) 
7) 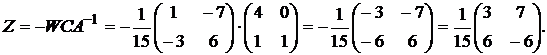
8) 
9) 
10) 
Таким образом, можно составить матрицу

Упражнения.
1. Найти обратные матрицы.
а)  б)
б)  в)
в) 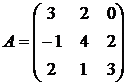
Ответы:
а)  б)
б) 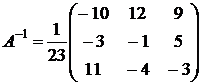
в) 