44 -

уравнение в частных производных (19.54) на два обыкновенных дифференциальных уравнения, из которых одно будет составлено относительно М, другое — относительно N. Подставим (19.55) в (19.54), учтя, что
Поэтому 

|

|
Умножим (19.66) на
Особенностью уравнения (19.57) является то, что первое слагаемое в нем представляет собой функцию только R, а второе слагаемое — функцию только θ. Сумма двух функций, из которых одна зависит только от R, а другая—только от θ, равна нулю для бесчисленного множества пар значений R и' θ [уравнение (19.57) годится для всех точек поля]. Это возможно тогда, когда каждая из данных функций равна нулю:

либо когда

Здесь р есть некоторое число, пока не известное.

|
| Интеграл первого из них: |

|
| Найдем интеграл второго уравнения: |

|
Таким образом, задача свелась к интегрированию уравнений (19.57') и (19.57"). Общее решение для φ согласно (19.55) равно произведению решений уравнений (19.57') плюс произведение решений для М и N по уравнениям (19.57"). Найдем решение уравнений (19.57'). Так как в (19.57') М зависит только от R, а N -—только от 9, то от частных производных можно перейти к простым (обыкновенным):
Покажем, что А3 непременно должно равняться нулю, так как только в этом случае в решении отсутствует слагаемое А3Intg 

Потенциал есть функция непрерывная и на конечном отрезке он не может измениться на бесконечно большую величину. Из физических соображений ясно, что потенциал точек оси z вблизи шара не может быть равен бесконечности. Между тем, если бы А3  0, то в решении
0, то в решении
для потенциала присутствовало бы слагаемое А3 Intg  , равное—
, равное— 
| Полное решение: |

для всех точек, у которых  = 0 (tg θ =0; In tg θ = —
= 0 (tg θ =0; In tg θ = —  ).
).
при 8 = 0 t при 6=0
Таким образом, частное решение для φ, вытекающее из ('19;57'), следующее:

Найдем решение уравнений (19.57"):


|
или,
Применим подстановку Эйлера М == CRn:


|

Подставим производные в уравнение

|
Или n2+n-p=0
Определим корни квадратного уравнения:

Значение р определим при интегрировании второго уравнения
(19.57  :.
:.


|
| Следовательно, р = 2. |
Решение его можно записать в виде N = В cos θ. Убедимся в этом путем подстановки и одновременно найдем значение р:
После нахождения числа р подставим его в (19.61) и найдем: п1 = 1 и пг = —2. Таким образом, совместное решение уравнений (19.57") дает следующее выражение для φ:
В (19.62) присутствуют четыре неизвестных постоянных: C1, C2, С3 и С4. Значения постоянных зависят от того, какой шар (проводящий или диэлектрический) внесен в поле *.
§ 19.40, Проводящий шар в равномерном поле. Для определения
четырех постоянных необходимо учесть не только условие на поверхности шара, но и условия на большом удалении от шара, теоретически
на бесконечно большом удалении от шара, или, как принято говорить,
условия на бесконечности.
Совокупность весьма удаленных от шара точек в условном смысле
рассматривается при этом как бесконечность. Если шар не заряжен,
то все. точки плоскости хоу, проходящей через центр шара, имеют
один и тот же потенциал. Обозначим его φ0.
При удалении от шара на большое расстояние z = R cos θ, по сравнению с которым радиус шара α весьма мал, возмущающее действие шара на поле либо вовсе не проявится (если суммарный заряд шара будет равен нулю), либо проявится как возмущение от точечного заряда (если шар будет иметь на себе суммарный свободный заряд Q). Потенциал φ на бесконечности определим так:
Первое слагаемое правой части (19.63) дает составляющую потенциала от заряда шара Q, слагаемое E0R cos θ учитывает прирост потенциала от напряженности равномерного поля Е0 на пути z = R cos θ. Так как решение (19.62) годится и для точек поля, весьма далеко (бесконечно далеко) удаленных от шара, то можно сопоставить выражения (19.62) и (19.63). 0ни должны давать один и тот же результат. Это будет только в том случае, когда соответствующие слагаемые в обоих выражениях равны. Из сопоставления следует, что

Сопоставление на бесконечности не дает возможности найти величину С4, так как в (19.63) нет слагаемого, изменяющегося обратно пропорционально второй степени R. Для нахождения С4 воспользу-
-------------------------------------------
* Задачи теории поля, в которых приходится решать уравнение в частных производных и из большого числа выбирать решения, удовлетворяющие граничным условиям, в математических работах принято называть краевыми задачами.
47

емся в условиях электростатики все точки поверхности шара имеют один и тот же потенциал. Это условие равносильно тому, что тангенциальная составляющая напряженности поля на поверхности шара равна нулю. При R= a
| Правая часть будет постоянной с изменением θ только при усло- |
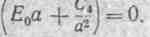 вии, что вии, что
|

| Таким образом, для всех точек диэлектрика |
Если Q=0, то на поверхности шара (при R — а) ЕR = -3E9 cos θ.
При θ=0 напряженность ER = - 3 E9; при 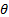 == 180° ЕR = 3EQ, т. е. в этих точках напряженность поля стала в три раза больше напряженности равномерного поля EQ в которое был внесен шар. На «экваторе» при θ = 90° напряженность, напротив» стала равной нулю. Таким образом, капелька воды, попав в бак трансформатора с масляным заполнением, вызовет значительное местное увеличение напряженности поля.
== 180° ЕR = 3EQ, т. е. в этих точках напряженность поля стала в три раза больше напряженности равномерного поля EQ в которое был внесен шар. На «экваторе» при θ = 90° напряженность, напротив» стала равной нулю. Таким образом, капелька воды, попав в бак трансформатора с масляным заполнением, вызовет значительное местное увеличение напряженности поля.


§ 19.41. Диэлектрический шар в равномерном поле. Если в равномерное поле помещен незаряженный диэлектрический шар, то как внутри шара, так и вне его нет свободных зарядов и потому поле описывается уравнением Лапласа. Полное решение (19.62) пригодно и для данной задачи. Величины, служащие для описания поля внутри шара, обозначим с индексом i, а величины, с помощью которых записывается потенциал во внешней по отношению к шару области,— с индексом е. Таким образом, для внутренней области
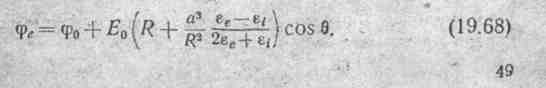
Надо найти 8 постоянных интегрирования. Потенциал на бесконеч
ности в этом случае φ= φ0 + E0R cos θ.
 для внешней области для внешней области
|
48,

Сопоставим последнее выражение с (19.66): C2е = φ0 и С3е = Е0 .
В § 19.14 было рассмотрено поле точечного заряда. Там было
показано, что потенциал в поле точечного, заряда изменяется обратно пропорционально R. Поэтому Cle/R — есть составляющая потенциала от суммарного заряда шара, рассматриваемого как точечный заряд. Так как суммарный заряд шара равен нулю, то в выражении для φе составляющая должна выпасть, т. е. С1е = 0.
Следовательно,
| Отсюда С4 == —Е0а3. |
В выражении (19.66) осталась неизвестной лишь постоянная C4е.
 Так как потенциал зависит только от R и 0, напряженность электрического поля имеет только две составляющих (см. § 19.8): Так как потенциал зависит только от R и 0, напряженность электрического поля имеет только две составляющих (см. § 19.8):
|
Рассмотрим выражение потенциала φi для внутренней области. Оно должно давать конечное значение для всех точек внутри шара. Это возможно только тогда, когда С1i = 0 и С4i =0 (если бы C1i  0, то слагаемое С1i/R в центре шара при R = 0 давало бы бесконечно большое значение). Постоянная С2i с точностью до которой определяется потенциал в рассматриваемом поле, равна аналогичной постоянной С2е = φ0 для внешней области. Таким образом, для внутренней области
0, то слагаемое С1i/R в центре шара при R = 0 давало бы бесконечно большое значение). Постоянная С2i с точностью до которой определяется потенциал в рассматриваемом поле, равна аналогичной постоянной С2е = φ0 для внешней области. Таким образом, для внутренней области

Оставшиеся неизвестными постоянные С4е и C3i найдем из гранич-
НЫХ: УСЛОВИЙ. Из равенства потенциалов φi и φе при R == а (это условие, как нетрудно, убедиться, эквивалентно.условию E1t=E2t) следует, что
 Из равенства нормальных составляющих вектора D на границе следует, что ' Из равенства нормальных составляющих вектора D на границе следует, что '
|
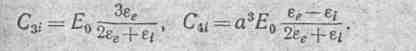 Совместное решение двух последних уравнений дает: Совместное решение двух последних уравнений дает:
|

.
| Т.е. |

| Потенциал внутренней области: |
| .Потенциал внутренней области: |
| .Потенциал внешней области: |
| Напряженность поля внутри шара: |
 Решая уравнение Лапласа в цилиндрической системе координат, Получим следующие формулы для определения потенциала внутри Решая уравнение Лапласа в цилиндрической системе координат, Получим следующие формулы для определения потенциала внутри
|
| цилиндра (φi) и вне цилиндра (φе): |
  Напряженность равномер- ного поля внутри цилиндра, направленная по оси х, Напряженность равномер- ного поля внутри цилиндра, направленная по оси х,
|


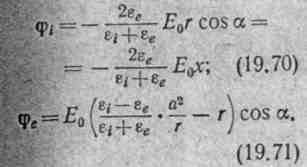
Напряженность Е направлена вдоль оси - z и не зависит от координат точки. Это означает, что поле внутри шара однородное. На рис. 19.23 изображены линии вектора D и эквипотенциальные линии (картина поля) для трех случаев:
а) когда в равномерное (до внесения шара) поле помещен незаряженный проводящий шар (рис.19.23,а);
б) когда в равномерное (до внесения шара) поле помещен диэлектрический шар, ε i которого больше εе окружающей среды (рис. 19.23, б);


в) когда ε i диэлектрического шара меньше εе окружающей среды (рис.19.23,в)
Как известно из § 19. 15, линии вектора D начинаются на свободных зарядах.Эти линии прерываются на поверхности металлического шара (см.рис.19.23,а) и проходят, не прерываясь, через диэлектрический шар (см.рис.19.23,б и в).
Если на рис.19.23,б и в вместо линий вектора D изобразить линии вектора напряженности поля E, то линии E частично претерпевали бы разрыв на поверхности шаров,так как истоком для E являются не только свободные, но и связанные заряды (см.формулу (19.21')
§ 19.43. Диэлектрический цилиндр в равномерном поле. Аналогично формулам § 19.41 выводятся формулы, позволяющие определить потенциал и напряженность равномерного поля, возмущенного внесением в него диэлектрического цилиндра (ось цилиндра перпендикулярна E0).
Пусть напряженность E0 равномерного (до внесения цилиндра) поля направлена параллельно оси х декартовой системы (рис.19.24,а). Поместим в это поле диэлектрический цилиндр так, чтобы ось цилиндра совпала с осью z.

В заключение отметим,
что если в равномерное поле
напряженностью Е0 внести
проводящий цилиндр радиу-
сом а, расположив его так, что продольная ось его будет перпендикулярна Е, то потенциал в области вне цилиндра

§ 19.43. Понятие о плоскопараллельном, плоскомеридианном и равномерном полях. В литературе можно встретить термины «плоскопараллельное поле», «плоскомеридианное поле» и «равномерное
поле» *.
Под плоскопараллельным полем понимают поле, картина которого (т. е. совокупность силовых и эквипотенциальных линий) повторяется во всех плоскостях, перпендикулярных какой-либо одной оси декартовой системы координат, т. е. в плоскопараллельном поле каротина поля не зависит от какой-либо одной координаты декартовой системы.
В качестве примера плоскопараллельного поля можно назвать поле двухпроводной линии (двух параллельных проводов). Если ось z декартовой системы направить вдоль оси одного из проводов, то потенциал φ не будет зависеть от координаты z.
* Физики и математики в термин «поле» вкладывают свое («профессиональное») содержание. Когда говорят о поле в физическом смысле (электромагнитном, гравитационном, тепловом, поле ядерных сил), то под ним понимают вид материи. Когда о поле говорится в математическом смысле, то имеется в виду поле величины, которой оно описывается. С чисто математической точки зрения поля могут быть векторные и скалярные, вихревые и безвихревые, плоскопараллельные, плоскомеридианные и др.
(51)
Под плоскомеридианным полем понимают поле, картина которого повторяется во всех меридианных плоскостях, т.е. картина поля не зависит от координаты а цилиндрической или сферической системы координат. В литературе встречается еще определение плоскомери-дианного поля как поля, образованного телами вращения с общей осью.
В качестве примера плоскомеридианного поля можно назвать поле образованное внесением металлического шара в равномерное до внесения шара поле (см. рис. 19.23), или поле диполя, о котором идет речь в примере 197. В обоих случаях потенциал зависит только от радиуса R и угла θ сферической системы координат, но не зависит от угла α.

Частным случаем плоскомеридианного поля является поле, в котором потенциал зависит только от какой-либо одной координаты сферической или цилиндрической системы координат.
В равномерном поле напряжённость одинакова во всех точках поля; т. е. величина ее не зависит от координат точки.
Равномерное поле Образуется, например, между обкладками плоского конденсатора, если в пространстве между ними отсутствуют свободные заряды и если пренебречь искажающим влиянием краев кон
денсатора.
Следует иметь в виду, что большинство встречающихся на практике полей не обладает ни одним из перечисленных видов симметрии и потому не может быть отнесено ни к плоскопараллельному, ни к плоскомеридианному, ни к равномерному полям.
| § 19.44. Графическое |
построение картины плоскопараллельного поля.
Аналитический расчет полей часто вызывает затруднения, например, кргда поверхности электродов имеют сложную форму.
 В этом случае картину поля строят графически. С этой целью сначала выясняют, не обладает ли изучаемое поле симметрией. Если она имеется, то картину поля строят только для одной из областей симметрии. Так, картина поля, образованного двумя проводящими взаимно
В этом случае картину поля строят графически. С этой целью сначала выясняют, не обладает ли изучаемое поле симметрией. Если она имеется, то картину поля строят только для одной из областей симметрии. Так, картина поля, образованного двумя проводящими взаимно
перпендикулярными относительно тонкими пластинками (электродами), построена на рис. 19.25, а только для верхней полуплоскости (в нижней полуплоскости картина повторяется).
| Для того чтобы слагаемые в скобке по величине были одинаковы, при построе- |
   нии должно быть выдержано соотношение нии должно быть выдержано соотношение
|


При построении руководствуются следующими правилами. 1. Силовые линии должны подходить к поверхностям электродов перпендикулярно. 2. Силовые и эквипотенциальные линии должны быть взаимно перпендикулярны и образовывать подобные ячейки поля (криволинейные прямоугольники), для.которых отношение средней длины
ячейки а к средней ширине этой ячейки b для всех ячеек должно быть приблизительно одинаковым, т. е. a 1lb1 = a2/b2 =....
Если число ячеек в силовой трубке обозначить п, а число трубок т (в примере п = 8, т = 2 х 10), то при соблюдении перечисленных правил разность потенциалов между соседними эквипотенциалями будет одинакова и равна  = U/n, где U — напряжение между электродами, а поток
= U/n, где U — напряжение между электродами, а поток  вектора D в каждой силовой трубке будет такой же, что и в соседней. Обозначим длину электродов в направлении, перпендикулярном рисунку, через l. Тогда
вектора D в каждой силовой трубке будет такой же, что и в соседней. Обозначим длину электродов в направлении, перпендикулярном рисунку, через l. Тогда
Отсюда
Напряжение между электродами U == E1a1 + Е2а2+... + Еnаn. Подставим в последнее выражение значения напряженностей поля Е1  Еп и учтем, что по построению a1/b1 = a2/b2 = an/bn = a/b. Получим
Еп и учтем, что по построению a1/b1 = a2/b2 = an/bn = a/b. Получим

Л -

|

|
Поток в одной силовой трубке


|
Емкость между электродами C= 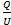

§ 19.45. Графическое построение картины плоскомеридианного поля. В пло
скомеридианном поле силовые линии также должны подходить к поверхностям электродов под прямым углом, а силовые и эквипотенциальные линии должны быть взаимно перпендикулярны. Однако в отличие от плоскопараллельного поля в образующйхся при построении ячейках поля в меридианной плоскости отношение аk к bk не одинаково для всех ячеек, а зависит от расстояния центра этой ячейки до оси вращения.На рис. 19.25, б изображена часть картины поля между двумя шарами. Каждая силовая линия при вращении вокруг общей оси образует поверхность вращения, а каждая силовая трубка занимает пространство между смежными поверхностями вращения.
Обозначим а k –длина ячейки вдоль силовой.трубки; bk —ширина ячейки;
n-число ячеек.вдоль силовой трубки; т — число силовых трубок. Запишем условие
равенства потока вектора D через ячейки силовой трубки  = 2πr1b1ε aE1 =
= 2πr1b1ε aE1 =
2πr2b2ε aE2=..'Напряжение между электродами
т.е. с увеличением
| расстояния центра ячейки от оси вращения отношение_аk/bk должно возрастать. Если это соотношение выдержано, то |
| расстояния центра ячейки от оси вращения отношение_аk/bk должно возрастать. Если это соотношение выдержано, то |


§ 19.46. Объемная плотность энергии электрического поля и выражение механической силы в виде производной от энергии электрического поля по изменяющейся координате. Положим, что в некоторый момент времени напряжение на конденсаторе равно и. При увеличении напряжения на конденсаторе на величину du заряд на одной из пластин конденсатора увеличится на величину dQ, а на другой -на величину —dQ: dQ = Cdu, -где С— емкость конденсатора.'
Для переноса заряда dQ источник энергии должен совершить работу, равную udQ=Cudu, которая затрачивается на создание электрического поля в конденсаторе.
Энергия, доставленная легочником при заряде конденсатора от, напряжения и =0 до напряжения и = U и перешедшая в энергию электрическогополя конденсатора,

Рассмотрим вопрос об объемной плотности энергии электрического поля. С этой адлью возьмем плоский конденсатор и положим, что расстояние между пластинами его равно х, а площадь каждой пластины с одной стороны равна S. Диэлектрическая проницаемость среды между пластинами εа. Напряжение между пластинами U. Пренебрежем искажающим влиянием краев конденсатора на поле [между пластинами. При этом условии поле моясно считать равномерным. Напряженность электрического поля по модулю Е = U/x.
Вектор электрической индукции по модулю D =εаЕ = Q/S. Емкость плоского
конденсатора С =  Для нахождения объемной плотности энергии электрического поля разделим энергию W
Для нахождения объемной плотности энергии электрического поля разделим энергию W  =
=  =
=  на объем V = Sх, «занятый полем». Получим
на объем V = Sх, «занятый полем». Получим

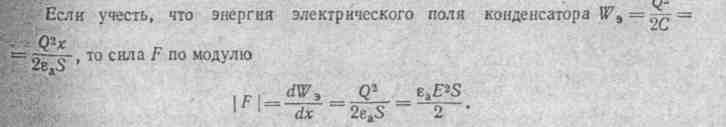
Таким образом, объемная плотность энергии электрического поля равна  ,
,
Если поле неравномерно, то напряженность будет изменяться при переходе от одной точки поля к соседней, но объемная плотность энергии поля будет по-прежнему равна
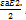 так как в пределах бесконечно малого объема поле можно считать равномерным. Выделим в поле элементарный объем dV. Энергия в этом объеме равна
так как в пределах бесконечно малого объема поле можно считать равномерным. Выделим в поле элементарный объем dV. Энергия в этом объеме равна  dV.
dV.
Энергия, заключенная в объеме V любых размеров, равна

В электрическом поле между заряженными телами действуют механические силы и их можно выразить в, виде производной от энергии поля по изменяющейся координате. На рис, 19.24, б изображен плоский конденсатор, который присоединен к источнику напряжения U. В Соответствии с предыдущим расстояние между пластинами назовем х, а площадь пластины — S. На каждую пластину конденсатора действует сила F. Под действием этих сил пластины конденсатора стремятся сблизиться. Сила, действующая на нижнюю пластину, направлена вверх, на верхнюю пластину — вниз.
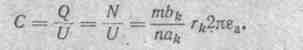
Положим, что под действием силы F нижняя пластина медленно, теоретически бесконечно медленно, переместилась вверх на расстояние dx и приняла положение, показанное пунктиром на рис. 19.24, б. Составим уравнение для баланса энергии при таком перемещении пластины. На основании закона сохранения энергии доставленная источником питания энергия dWи должна равняться сумме трех слагаемых: 1) работе силы F на расстоянии dx: Fdx= Fdx; 2) изменению энергии электрического поля конденсатора dW3; 3) тепловым потерям от тока  , который протекает по проводам с сопротивлением R в течение времени от 0 до
, который протекает по проводам с сопротивлением R в течение времени от 0 до  : dWи = Fdx + dW
: dWи = Fdx + dW  +
+  Rι2dt
Rι2dt