построение картины плоскопараллельного поля. 2 глава

Так как по условию проведения эксперимента пластина конденсатора переме­щается вверх теоретически бесконечно медленно, то изменение зарядов на пластинах также происходит весьма медленно, а следовательно, и проходящий через конденсатор ток смещения бесконечно мал. Другими словами, тепловыми потерями

Rι²dt в силу их малости в уравнении энергетического баланса можно пренебречь

Таким образом, силу F можно.выразить в виде производной от разности энер­гий (W_и— W ) по изменяющейся координате х.

В общем случае при перемещении пластины могут изменяться и напряжение «между пластинами U и заряд Q

Рассмотрим теперь два характерных частных случая перемещения пластины конденсатора. В первом конденсатор отсоединен от источника напряжения и переме­щение пластины происходит при неизменных зарядах на пластинах. Во втором пере-_: мещение пластины происходит при неизменном напряжении между пластинами (конденсатор присоединен к источнику неизменного напряжения U).

Пе р в ы й случай. Так как конденсатор отсоединен от источника энергии,

то последний энергии не доставляет и потому dW_n = 0. При этом F= -

Таким образом, сила, действующая на пластину, равна взятой с обратным знаком производной от энергии электрического поля конденсатора по изменяющейся

координате. Знак «минус» свидетельствует о том, что в рассматриваемом случае

работа силы производится за счет убыли энергии в электрическом поле конденса-

Второй случай. Энергия, доставляемая источником питания при U = =rconst, dWи = UdQ = U2dC, где dC — приращение емкости, вызванное умень­шением расстояния между пластинами, на величину dx.

тора

Сила, действующая на пластину конденсатора во втором случае, равна силе, действующей пластину конденсатора в первом случае. На единицу повеохности

конденсатора действует сила

выражает собой не только плотность

Обратим внимание на то, что величина

энергии электрического поля, но и числе силе, действующей на единицу, поверхности пластины конденсатора. Действующие на пластины конденсатора силы можно рассматривать как результат проявления сил продольного сжатия (вдоль силовых трубок) и сил бокового распора (поперек силовых трубок). Силы продоль­ного сжатия стремятся укоротить силовую трубку, а силы бокового распора — расширить ее. На единицу боковой поверхности силовой трубки действует сила, численно равная ε_аE²/2. Эти силы проявляются не только в виде сил, действующих на пластины конденсатора, но также в виде сил на границе раздела. двух диэлектриков. В этом случае на границе раздела действует сила, направленная в сторону диэлектрика с' меньшей диэлектрической проницаемостью.

§ 19.47. Энергия поля системы заряженных тел. Энергия поля, образованного системой п заряженных тел, имеющих потенциалы φ₁.... φ_n и заряды q_1…..q_n

Вывод формулы основан на том, что энергия поля равна работе внешних сил, затраченной на перенос зарядов из бесконечности (где φ = 0) в точки поля, в которых они будут находиться, и на прин­ципе наложения. Используя формулу (19-48), сначала находим ра­боту при переносе заряда q₁,_ полагая, что заряды всех остальных тел равны нулю. Затем находим работу при переносе заряда q₂, пола­гая q₁ == const и q₃ = q₄ = q_n= 0 и т. д. Суммируя все работы, получаем формулу (а).

Заметим, что заряды на проводящих телах, находящихся в ди­электрике, всегда распределяются по поверхностям этих тел так, что энергия образовавшегося между этими телами электрического поля минимальна (теорема Томсона).

Пример 181 а. Два провода диаметром 10 мм расположены в воздухе параллельно друг другу (рис. 19.24, в). Расстояние между осями проводов d — 20 мм. Заряд каждого провода на метр длины 10^-8 К. Левый провод несет положительный заряд, правый — отрицательный. Найти наибольшую и наименьшую плотности заряда на поверхности провода.

Р е ш е н и е. Находим положение электрических осей: х = 1,35 мм. Плотность заряда на поверхности металла а = D = ε_аЕ. Следова­тельно, а будет больше там, где Е больше.

Если учесть, что напряженность поля, создаваемая положительным зарядом, направлена от этого заряда, а напряженность поля,

создаваемая отрицательным зарядом, направлена к заряду, то ясно,

что наибольшая напряженность поля будет в точке А, наименьшая —

в точке В. Напряженность поля в точке А равна сумме напряженностей от обоих зарядов, а в точке В — разности напряженностей:

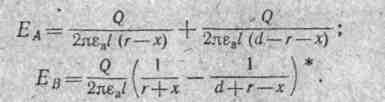
Отсюда D_A = Ơ_А = ε _аE= 0,544 мкК/м²,Dв= Ơ_В= ε _аE _В = 0,186 мкК/м².

Таким образом, плотность заряда в точке А в 2,92 раза больше, чем плотность заряда в точке В.

Пример 181 б. По условию предыдущей задачи найти градиент потенциала в точке М (расположенной посредине между проводами. на линии, соединяющей их центры).Р е ш е н и е. Так как Е = — grad φ, то модуль grad φ равен модулю Е, а направление grad φ противоположнонаправлению

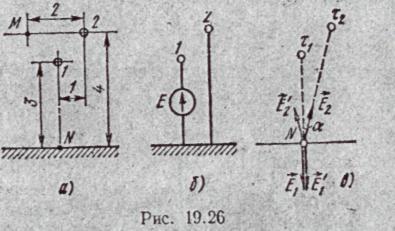Е. В точке М

Направления E и grad φ даны на рис. 19.24, в.

Пример 182. Определить частичные емкости на один

метр длины двухпроводной линии. Геометрические размеры (в метрах)
см. на рис. 19.26, а. Радиусы проводов 6 мм.

Решение. В соответствии с формулой (19.48):

 

 

Отсюда

 

 

Здесь

 

______________________________

Для воздуха ε_{а =} ε_{0 (}ε₌₁₎

Таким образом,

Следовательно, для двухпроводной линии:

Аналогичным путем найдем:

По формуле (19.48') найдем:

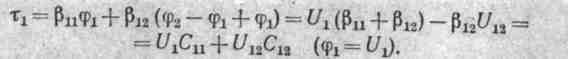
Пример 183. Провод 1 примера 182 соединен с землей через источ­ник э. д. с. Е = 127 В. Провод 2 соединен с землей проводником, так что его потенциал равен нулю (рис./ 19.26, б). Определить за­ряды на проводах 1 и 2 на один погонный метр.

Заряд первого провода τ₁ =127•0,852 • 10^-11 = 1,08•10^-9 К/м. Заряд второго провода τ ₂ = — 0,191 •10-¹¹•127 = -0,242-10 ^-9 К/м.

Пример 184. Заряд τ₁ на единицу длины провода 1 (см. рис. 19.26, а) равен 2•10^{- 9} К/м. Заряд τ ₂ на единицу длины провода 2 равен—10~⁹ К/м. Определить потенциал точки М, полагая потенциал земли равным нулю.

Решение.

Пример 185. Определить плотность наведенного заряда на поверхности земли в точке N (см. рис. 19.26, а), полагая, что заряды на проводах такие же, как и в примере 184.

Решение. В соответствии с формулой (19.33) плотность заряда на поверхности проводника равна напряженности в, этой точке, умноженной на ε_а = ε₀ Напряженности поля в точке N (рис. 19.26 в) равна геометрической сумме напряженностей от четырех зарядов —от заряда τ₁ (обозначим ее Е₁), от заряда τ₂ (Е₂) и зеркальных изображений этих зарядов Е'₁ и Е'₂: Е= E₁ + Е₂ + Е'₁ + Е'₂

Напряженности E₁ и Е'₁ направлены по одной прямой (по вертикали). Для нахождения проекций E₂ и Е'₂ на вертикаль умножаем E₂и Е'₂ на cos α. Плотность заряда

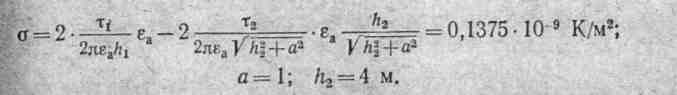
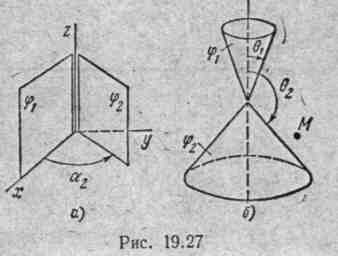
Пример 186. Две металлические пластинки (теоретически бесконечной протяженности) находятся в воздухе (рис. 19.27, а), образуя,

не соприкасаясь, двугранный угол α₂. Потенциал первой пласти­ны φ₁, второй φ ₂. Вывести формулы для определения φ и Е в любой точке поля внутри двугранного угла, а также формулу для определения плотности заряда на пластинках. Дать числовой ответ при φ₁= 0, φ₂ = 100 В, α₂ = 30°.Решение. Поскольку граничные поверхности проще всего можно описать в цилиндрической системе координат, то решение будем проводить именно в этой системе. В пространстве между пластинами отсутствуют свободные заряды, поэтому поле подчиняется уравнению Лапласа [см. уравнение (19.30)].

Потенциал φ зависит только от угла α и из условий симметрии не зависит от координаты z и радиуса r цилиндрической системы

Согласно этому уравнению, φ= С₁α + С₂. По условию, при

α = 0; φ = φ₁= 0, а при α= α₂ φ = φ₂ = 100 В. Следовательно, С₂=0; С₁= 100 =600/π и φ=600/π •α π/6

Напряженность поля имеет только одну альфовую составляющую

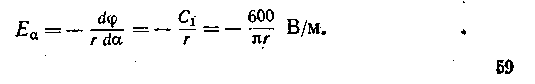
Пример 187. Две металлические конусообразные воронки находятся в воздухе, обращены остриями друг к другу и не соприкааются (рис. 19.27, б). Угол 30°, 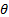₂ = 135°, потенциал первой воронки φ₁=0, потенциал второй воронки φ ₂ = 1000 В. Вывести формулу для определения φ и Е в пространстве между воронками и найти по ним Е и φ в точке М с координатами R = 2 см и 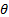= 120°.

Решение. Воспользуемся сферической системой координат, поскольку поверхности воронок проще всего описываются именно в этой системе. В пространстве между воронками отсутствует объемный заряд, поэтому поле описывается уравнением Лапласа [см. фор­мулу (19.31)1.

В силу симметрии φ зависит только от угла 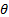и не зависит от ра­диуса R и угла α — двух остальных коорлинат сферическрй системы.

Найдем постоянные интегрирования C_t и С₂. При 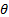= 30° φ = 0,
при 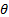=135° φ= 1000 В. Следовательно, 0 = С₁ In tg 15° + С₂;
1000 == С₁In tg 67°30'+ С₂

Отсюда С₁= 461 В, С₂ = 608 В. Потенциал точки М: φ_М= 461 In tg 60° + 608 = 856,5 В..

Напряженность поля имеет только 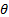-оставляющую:

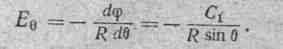
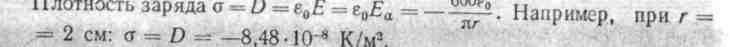
Пример 189. В цилиндрическом конденсаторе с воздушной изоляцией вокруг внутреннего электрода радиусом r₀ располагается

заряд короны с объемной плотностью pК/см³. Наружный радиус

короны r₁ (рис. 19.29). Радиус наружного электрода r₂. Потенциал

внутреннего электрода φ₀, потенциал наружного электрода φ₂.

Вывести формулу для определения φ в пространстве, занятом объем­ными зарядами (назовем его областью I), и в пространстве, не занятом свободными зарядами (область II).

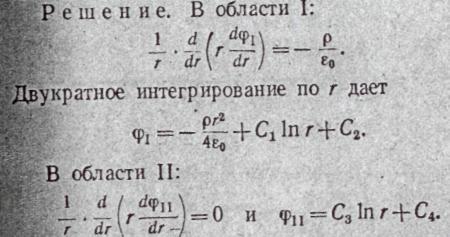
Напряженность в точке М: Е_θМ = =-26,6 кВ/м.

Пример 188. В вакууме на расстоянии 2 см друг от друга расположены два плоских электрода (рис. 19.28). Правый электрод заземлен. а левый соединен с плюсом батареи, э. д. с. которой 200 В;

отрицательный зажим батареи заземлен. В про­-
странстве между электродами распределен
объемный заряд с плотностью p = —α ε₀ х,
где_α — 30 кВ/см³; х— расстояние от левой
пластины (см. рис.; 19.28). Требуется найти
закон изменения потенциала в пространстве
между электродами. ',"

Ре ш е н и е. Полагаем, что размеры элек­тродов много больше расстояния между ними. Направляем ось х, как показано на рис. 19.28.

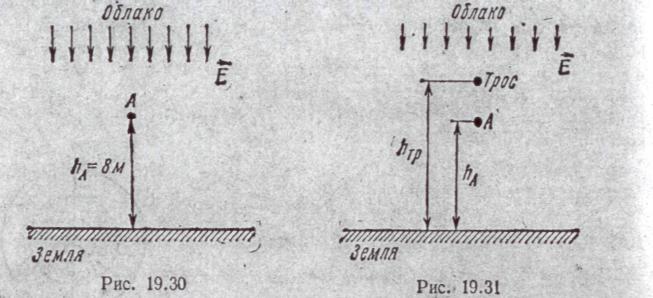
Пример 190. Над поверхностью земли расположилось положительно заряженное грозовое облако. Пространство между облаком и землей можно рассматривать как огромных размеров плоский кон­денсатор. Напряженность поля E в нем направлена от облака к земле. Найти потенциал точки А, расположенной на расстоянии 8 м от поверх­ности земли, в двух случаях: 1) когда над поверхностью земли не про­тянут заземленный трос,(рис. 19.30) и 2) когда над поверхностью земли над точкой А на высоте 10 м от земли протянут заземленный стальной трос диаметром 10 мм (рис. 19.31).

Пример 191. В равномерное поле с напряженностью Е₀ = 10³ кВ/м внесен незаряженный металлический шар радиусом а = 1 см. Найти E_R и Е_θ в точке А. Координаты точки А: R = 2 см и θ= 30°. Решение. В соответствии с формулами § 19.40 имеем:

Пример 192. В воздухе создано равномерное электрическое поле Напряженностью Е₀ = 10³ кВ/м. В это поле диэлектрический цилиндр (ε_i= 4ε₀) поместили так, что его ось перпендикулярна полю. Найти напряженность поля E_i внутри цилиндра. Решение. Воспользуемся формулой (19.72):

Пример 193. В некоторой области пространства имеется поле, потенциал которого зависит только от координаты х декартовой системы: φ = 5х³ — 60 х^г.

Найти закон изменения плотности свобод­ных зарядов в этом поле.

Р е ш е н и е. Уравнение Пуассона, опиывающее поле, можно записать так: d²φ/dx²= -p_своб./ε_аДважды дифференцируем φ по х:

Следовательно, р_сво6 = (—-30 х + 120) е_а.

Пример 194. Вывести формулу для опре- деления напряженности и потенциала поля,

создаваемого заряженной осью длиной l (рис. 19.32). Заряд на
единицу длины оси равен τ. -

Решение. Определим Е и φ в произвольной точке k. Распо-I ложим оси декартовой системы координат в соответствии с рис. 19.32.

Выделим отрезок оси длиной dx, на нем будет заряд rdx. В силу малости dx будем считать этот заряд точечным и по теореме Гаусса найдем создаваемую им напряженность поля в точке к:

 

 

Угол β отсчитываем от положительного направления dx к поло­жительному направлению радиуса R (последний направлен от dx к точке k) (верхний угол β на рис. 19.32 указан ошибочно).

§ 19.48. Метод средних потенциалов. Как уже говорилось в электростатиче­ском поле, образованном системой заряженных проводящих тел, все точки поверх-

ности каждого тела имеют одинаковый потенциал, а по­верхностная плотность зарядов т в общем случае изме­няется от точки к точке.

В тех случаях, когда неравномерность распределения зарядов по поверхности тела невелика, для подсчета емкостей иногда пользуются методом средних потенциалов (приближенный метод). В. его основу положено заведомо неправильное предположение, что-на поверхности каждого тела заряды распределены с одинаковой плотностью, а различные точки одного и того же проводящего тела имеют неодинаковые потенциалы. Это предположение дает воз­можность относительно легко найти среднее значение потенциала φ_ср. тела и по известному заряду тела найти его емкость. Результат оказывается. близким к истинному.

Пример 195. Определить емкость уединенного пря­мого проводника длиной l и радиусом r

единицу длины и помести h = r). Тогда

Решение. Воспользуемся формулой для потенциа­ла произвольной точки k. полученной в примере 194. Сосредоточим заряд на оси провода с плотностью τ на и точку k (рис. 19.32) на поверхность провода (т.е. примем

 

По определению (§ 19.29), заряд уединенного тела τl = φ _ср.С. Поэтому емкость уединенного цилиндрического провода

Пример 196. Вследствие неравномерного нагрева диэлектрическая проницаемость изоляции коаксиального кабеля (см.-рис, 19.33) изменяется в функции' радиуса r следующим образом: ε _а = т/r. Вывести формулы для определения напряженности электрического поля Е и смещения D. Радиус жилы кабеля r₁, внутренний радиус оболочки r₂, напряжение между жилой и оболочкой U. Объемный заряд отсутствует.

Решение. Воспользуемся теоремой Гаусса [формула (19.20)] в дифферёнциальной форме [применять уравнение Лапласа в данном случае нельзя, так как оно выведено при условии, что ε _а = const, (см. § 19.15)].-В формуле (19.24) заменим Е на D и учтем, что D имеет только одну r-составляющую и в силу симметрия не зависит от координат r и α. Будем иметь

Отсюда следует, что rD_r = rD = С; D = С/r, где С — некоторая постоянная. Таким образом, D изменяется обратно пропорционально радиусу. Напряженность поля E = D/ε_a = C/m, т.е. напряженность поля—величина постоянная. Определим постоянную С. Для этого воспользуемся тем, что отсюда

Графики изменения Е, D и φ см. на рис. 19.33.

Обратим внимание на то, что если бы диэлектрическая проницаемость ε_а изо­ляции коаксиального кабеля примера 196 была постоянной величиной (не являлась бы функцией r), то имели бы место следующие зависимости:

т. е. в этом случае напряженность поля была бы не постоянна, а изменялась обратно
пропорционально радиусу, потенциал φ изменялся бы не линейно в функции r.
а.по логарифмическому закону. _

Пример 197. Вывести формулы для расчета поля диполя.

Решен и е. Диполь изображен на рис. 19.34. Расстояние между

зарядами обозначим через l. При решении воспользуемся сфериче-
3 Зак. 1730

ской системой координат. Обозначим расстояние от произвольной точки а до заряда +q через R_1, до заряда — q — через R₂ и до сере­дины диполя — через R. Угол между вертикалью и радиусом R θ.Потенциал точки а определим как потенциал в поле двух точечных зарядов:

Таким образом, в поле диполя при R I потенциал ср изменяется обратно пропорционально второй, а напряженность — обратно про-

порционально третьей степени расстояния R рассматриваемой точки до диполя;φ и Е являются функциями угла θ.

Картина поля диполя изображена на рис. 19.35. Напряженность поля в некоторой произвольной точке а равна геометрической сумме напряженностей E₁ и E₂ от зарядов +q и — q. Если воспользуемся сфе­рической системой координат, то напряженность поля в той же точке. а можно представить в виде суммы напряженностей E_R и Е_в; E_R на­правлена вдоль радиуса R, а Е_θ имеет направление θ.

Пример 198. Вывести формулы для определения величины напря­женности поля и емкости двухслойного плоского конденсатора рис. 19.36, а также построить графики изменения модуля вектора напря­женности электрического поля Е, модуля вектора электрической индукции D и потенциала φ в функции расстояния х.

Толщина первого слоя диэлектрика d₁ второго — d₂. Абсолютная диэлектрическая проницаемость первого слоя ε_a1, второго слоя ε_a2. Принять ε_a1= 2ε_а2 и d₂ — 1,5 d₁

Ре ш е н и е. Все величины, относящиеся к первому слою, обозначим индексом 1, а ко второму слою—индексом 2. Поло­жим, что разность потенциалов между обкладками конденсатора равна U.

Искажающее влияние краев конденсатора на поле учитывать не будем. При этом условии в каждом слое поле будет равномерным.В силу того что нормальная составляющая вектора D непрерывна, имеем D_ln = D_2n.. Но D_ln = ε_a1E_1; D_2n = ε_a2E₂. Следовательно,

ε_a1E₁= ε_a2E₂ (а)

Таким образом, отношение напряженностей обратно пропорционально отношению 'электрических проницаемостей.

Графики зависимостей D, Е и φ от рас­стояния х изображены на рис. 19.36.

Уравнение (а) связывает две пока неиз­вестные величины E₁ и Е₂. Второе уравнение относительно Е₁ и Е₂ составим, исходя из того, что

 

Для нормальной работы конденсатора необходимо, чтобы напря­женность электрического поля ни в первом, ни во втором слоях кон­денсатора не достигла значения напряженности, при котором проис­ходит пробой данного диэлектрика.

Напряженность равномерного поля, при которой происходит пробой

данного диэлектрика, принято называть пробивной напряжен­ностью. Пробивная напряженность диэлектриков, особенно газооб­разных, сильно зависит от температуры и давления. Пробивная напряженность воздуха равна 30 кВ/см при нормальном атмосферном Давлении и температуре 18° С.

При выводе формулы для емкости двухслойного плоского конденсатора на границу раздела двух диэлектриков мысленно поместим бесконечно тонкий металлический листок. Эта операция вполне допустима, так как поверхность раздела диэлектриков как была экви­потенциальной поверхностью до помещения листка, так и остается ею после помещения на нее листка; причем значение потенциала ее при этом не изменится.

После проведения такой операции (ее иногда называют способом

отвердения) емкость двухслойного конденсатора можно: подсчитать

как емкость двух последовательно включенных конденсаторов С₁

и С₂; С₁ — емкость первого слоя конденсатора, С₂ — емкость второго

где S— площадь одной пластины конденсатора с одной стороны. Емкость двух последовательно, включенных конденсаторов

слоя конденсатора:

§ 19.49. О расчете электрических полей, создаваемых диэлектриками, сохраняю­щими остаточную поляризацию при снятии внешнего поля. Поле, которое создает

однородно поляризованный диэлектрик с остаточной поляризацией P (электрет, сегнетодиэлектрик) (на рис. 19.37, а он изображен в виде цилиндра длиной и площадью поперечного сечения. S) на ос­новании § 19.14.будет таким же; как поле воздушного конденсатора, изображенного на рис. 19.37, б. Площадь пластин этого конденсатора равна S, расстояние между ними , заряды на пл,астинах равны соответственно P S.