электромагнитного поля и излучение

ЭЛЕКТРОМАГНИТНОЙ ЭНЕРГИИ

§ 25.1. Вывод уравнений для Аи φ в переменном электромагнит-

ном поле и их решение. Переменное электромагнитное поле создается токами и зарядами, зависящими не только от координат, но и от времени. Рассмотрим, каким уравнениям подчиняются, векторный и скалярный потенциалы А и φ в переменном электромагнитном поле, С этой целью выпишем систему уравнений Максвелла

В (25.10) в качестве градиента скалярной функции взят grad φ. Объясняется это тем, что уравнение (25.10) должно быть справедливо и для статического поля. А так как в статическом поле ∂А/∂t =0, то

выражение, которое получается, из (21.10) для статического поля, должно совпадать с известным из электростатики выражением: Е = — grad φ.

В соответствии с (25.10) можно сказать, что в переменном электро- магнитном поле напряженность электрического поля имеет две состав-

ляющие. Одна из них (—∂А/∂t ) обусловлена переменным магнитным

 

т.е из (25.10) получили (25.10') — закон электромагнитной индукции

Обратим внимание на то, что формула (25.10), определяющая Е, записана для случая неподвижных тел и сред и при отсутствии сторонней напряженности поля Е_стор. возникающей, например, при соприкосновении проводящих тел различного химического состава или имеющих неодинаковую температуру.

В более общем случае,когда тело или среда движется со скоростью v в магнитном поле, индукции В ( vи В измеряются в одной и той же системе координат, а скорость v значительно меньше скорости света) и когда в данной точке поля имеется Е_стор, результирующая напряженность поля будет состоять, из четырех компонент: Е = — grad φ — ∂А/∂t + Е_стор. + Первые два слагаемых имеют тот же смысл, что и в (25.10), третье - сторонняя напряженность поля, четвертое – магнитная составляющая силы Лоренца, представляющая собой силу, действующую на единичный заряд, двигающийся со скоростью v в магнитном поле индукции В. Все четыре компоненты Е в одной и той же точке поля одновременно, как правило, не возникают.

 

Вектор-потенциал представляет собой функцию, ротор которой равен В. В гл. 21 отмечалось, что вектор-потенциал А должен быть подчинен определенному условию, а именно: в постоянном магнитном поле div А = 0, т. е. линии вектора представляют собой замкнутые сами на себя линии.

* Первую из них можно назвать вихревой составляющей, вторую — потенциальной (или кулоновой).

В переменном электромагнитном поле таким требованием к век­тору-потенциалу является требование (калибровка Лоренца):

Для того чтобы убедиться в том, что уравнение (25.12) совпадает с уравнением непрерывности (22.3), проделаем следующие выкладки. Применим оператор □² к обеим частям уравнения (25.12):

 

Нетрудно убедиться в том, что для неизменного во времени поля условие (25.12) сводится к условию dtv А = 0. В дальнейшем будет показано, что это условие является уравнением непрерывности div = = — ∂ρ/∂t (§ 22.3), записанным в иной форме.

Вместе с тем уравнение (25.12) свидетельствует о том, что в пере­менном электромагнитном поле между векторным потенциалом А и скалярным потенциалом φ существует определенная связь и что функ­ции А и φ зависят друг от друга.

С учетом (25.12) уравнение (25.11) приобретает вид:

и называется уравнением Даламбера.

Если А не является функцией t, то ∂²А/∂t² = 0 и уравнение (25.13)

переходит в уравнение Пуассона.

Уравнение (25.13) является неоднородным векторным волновым уравнением. Его часто записывают в иной форме:

²А= —μ_а . (25.13')

1 д²

Оператор □² = ²— 1/ v^{2 2}/∂t²называют четырехмерным лапласиа­ном (за четвертое измерение принимают время t).

Выясним, какому уравнению в переменном электромагнитном поле подчиняется потенциал φ. С этой целью в уравнение (25.4) вместо на­пряженности Е подставим ее эквивалент по (25.10):

div(-∂А/∂t-gradφ)= ρ/ε_а или -∂/∂t divА - div grad φ=ρ/ε_а

Но divА=-1/v² ∂φ/∂t и, следовательно, -∂/∂t divА= 1/v² ∂²φ/∂t²

В свою очередь div grad φ = ²φ. Поэтому уравнение (25.4) приобретает следующий вид: ²φ - 1/v² ∂²φ/∂t²= - ρ/ε_а

 

Таким образом, в переменном электромагнитном поле скалярный потенциал φ удовлетворяет неоднородному волновому уравнению (25.14). Если поле статическое и потенциал не является функцией времени, то ( ∂²φ )/(dt²) = 0 и уравнение (25.14) переходит в уравнение Пуассона ²φ = — ρ/ε_а, обсуждавшееся в § 19.19.

 

Причем функции и f₂ могут быть любыми, лишь бы они позво-
ляли дважды дифференцировать их по t и z. Вид функций опреде-
ляется граничными условиями..

Напомним, что о волновом уравнении* (25.17') уже говорилось при рассмотре-
нии вопроса о переходных процессах в линиях с распределенными параметрами
в гл. XII.

 

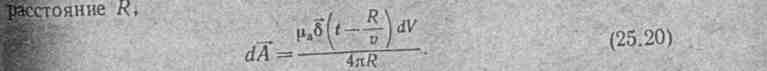
Обсудим решение уравнения (25.13). В общем случае это уравнение можно разбить на три уравнения для трех проекций вектора-потенциала*. Каждое из уравнений в проекциях будет составлено относительно скалярной величины (проекция вектора есть величина скалярная). Общее решение для каждой из проекций проводится точно так же, как проводилось решение для скалярной величины φ, но вместо объемного заряда будет участвовать соответствующая проек­ция плотности тока и μ _авместо 1/ε_а.

После умножения решений на соответствующие орты и сложения

окажется, что составляющая вектора потенциала от элемента тока

dV в некоторой точке пространства, удаленной от элемента тока на

Для получения результирующего значения А необходимо

геометрически просуммировать составляющие от всех элементов тока

§ 25.2. Запаздывающие потенциалы переменного электромагнитного поля. Рассмотрим, в чем состоит физический смысл выражений (25.18) и (25.20). Электромагнитная волна распространяется со скоростью v. Расстояние R она пройдет за время R/v. Поэтому значения составляющей потенциалаφ в переменном электромагнитном поле в некоторой точке, удаленной от заряда на расстояние R в момент времени t, определяется значением заряда в момент времени (t —R/V)

Также следует понимать и выражение dА=

В силу конечной скорости распространения электромагнитное волны значение вектора-потенциала от элемента тока dVв точке удаленной от элемента тока на расстояние R, изменяется с запаздыванием во времени на величину R/v. Поэтому потенциалы переменного электромагнитного поля называют запаздывающими потенциалами.

Так как скорость распространения: электромагнитной волны в дна электрике очень велика (в воздухе v 300 000 км/с), то запаздывание проявляется заметно только при значительных R. При малых R запаздывание настолько незначительно, что им практически можно пре- небречь.

Наиболее часто понятием запаздывающих потенциалов пользуются в радиотехнике при рассмотрении вопросов, связанных с.излучением электромагнитной энергии.

В переменном электромагнитном поле с учетом явления запазды- вания:

Ток i может изменяться во времени по любому закону. С практи­ческой точки зрения наиболее интересен синусоидальный закон из- менения тока во времени, поэтому полагаем:

§25.3. Комплексная форма записи запаздывающего векторного потенциала. В гл. 21 [см. уравнение (21.27)] отмечалось, что состав- ляющая векторного потенциала от элемента линейного тока idl

Ток можно представить в показательной форме I _m e^iωt,где 1_m = 1_mе ⁱ (строго говоря, надо было бы написать еще символ взятия мнимой части, но его часто опускают).

Ток i ( = I _m sin или в показательной форме

I _m e^iω Следовательно, комплексную амплитуду вектор-потен-

циала от элемента тока dlI_msin (ωt + )можно записать Аналогично, если электрические заряды, создающие поле, ме­няются во времени по синусоидальному закону, то комплексная амплитуда потенциала φ от объемного заряда р_т e^iωtdV

§ 25.4. Излучение электромагнитной энергии.

Рассмотрим вопрос об излучении электромагнитной энергии элементом тока. Пусть по отрезку проводника длинной dl, находящемуся в воздухе (ε_а = ε₀, μ _a -= μ₀), протекает ток lI_msin (ωt + ) (рис. 25.1). Далее будем пользоваться цилиндрической и отчасти сферической системами координат. Ось z цилиндрической системы направим вдоль проводника. Пусть положительное напра­вление тока по проводнику совпадает с положительным направлением оси z.

Найдем значение вектора-потенциала в произвольной точке, уда-1енной от элемента тока на расстояние R. В соответствии с (25.22)

Направление dA * совпадает с направлением вектора dl (вдоль оси г). Найдем магнитную индукцию в произвольной точке поля:

В= rot А

Из формулы (25,24) следует, что магнитная. индукция имеет α-е направление.

Для нахождения комплекса магнитной' индукции надо вычислить

— зависит в явном виде от R, а Не от r. Поэтому

Для любой точки пространства справедливо, очевидно, соотношение, вытекающее из теоремы Пифагора,

Продифференцируем (25:26) по r, получим

 

Выражение (25.28) можно переписать и в ином виде, перейдя к мгновенным значениям:

Формула (25.28') позволяет сделать вывод, что в любой точке пространства магнитная индукция от элемента переменного тока имеет две составляющие, одна из них бывает обратно пропорционально квадрату радиуса и изменяется по закону синуса во времени, другая бывает обратно пропорционально первой степени радиуса и изменяется по закону косинуса во времени. Найдем закон изменения напряженности электрического поля, соответствии с первым уравнением Максвелла:

 

Для того чтобы получить проекции Е на направление R и , необ­ходимо соответствующие проекции rot H разделить на Jωε₀ [см. урав­нение (25.29)]:

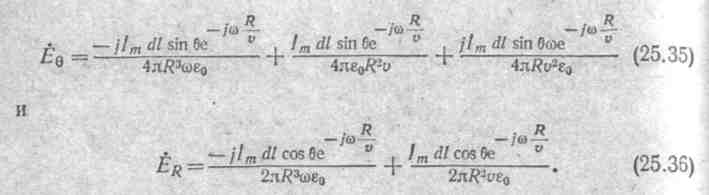
Таким образом, напряженность электрического поля имеет две составляющие: одна направлена по 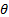, другая — по R; E _θсодержит три слагаемых [см. уравнение (25.35)], изменяющихся обратно про­порционально соответственно, третьей, второй и первой степеням рас­стояния R; Е_R состоит из двух слагаемых, Изменяющихся обратно

пропорционально R³ и R². Частное = = = .Отношение

модуля первого слагаемого в (25.33) к модулю второго равно 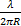(λ-длина волны)

 

Если R λ/2π, то первым слагаемым по. сравнению со вторым

можно пренебречь, если R λ/2π, то наоборот, можно пренебречь

 

вторым слагаемым. Аналогичные соотношения имеют место между модулями слагаемых в (25.34).

Принято все поле делить на ближнюю, среднюю и дальнюю зоны.

Для ближней зоны R λ/2π; для дальней R λ/2π.В средней зоне R

соизмеримо λ/2π. В соответствии с этим для ближней зоны

 

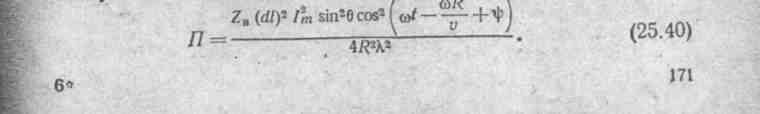
Таким образом, в дальней зоне, т. е. в зоне, для которой R λ/2π), напряженность магнитного поля имеет только одну α-ю

составляющую, а напряженность электрического поля — только одну θ-ю составляющую [см; уравнение (25.38)]. Если провести сферу радиусом- R, то во всех точках этой сферы (назовем ее эквифазной поверхностью) H имеет одну и ту же фазу колебания в какой-то конкретный момент времени (фаза колебания определяется аргументом косинуса), Амплитуда H для точек сферы R — const различна, она зависит от угла θ; на «полюсах» при θ = 0 и при θ = 180° амплитуда колеба-

ния для любого момента времени равна нулю, так как sinθ = sin180 =0 амплитуда колебания максимальна на «экваторе» сферы при θ = 90 По фазе Н и Е совпадают (см.уравнение (25.39)). Модуль Е в ₀ / ε ₀₌Z _В раз больше модуля Н, т.е. Е=НZ_В. Диаграмму зависимости модуля Е или Н в дальней зоне от угла θ принято называть диаграммой направленности. Она будет представлять собой объемную фигуру — тор, сечение которого плоскостью, проходящей через полярную ось, представляет собой две соприкасающихся окружности (рис. 25.2, а). Составим выражение вектора Пойнтинга для дальней зоны: П = |Е_θН_α] = ПR

Векторное произведение двух векторов, один из которых имеет θ-енаправление, а другой — α-е, дает вектор П, направленный по радиусу (рис. 25.2, б).. Так как Н и Е в дальней зоне совпадают по фазе, то с изменением направления Н на противоположное (Н изменяется во времени по косинусоиде) одновременно меняется на противоположное и направление вектора Е. Но вектор П своего направления не меняет, он все ремя направлен вдоль радиуса. Найдем величину модуля вектора Пойнтинга. С этой целью умножим модуль Е на модуль Н:

Подсчитаем поток вектора Пойнтинга через сферическую поверх­ность радиусом R. Элемент d S сферической поверхности радиусом R направлен по радиусу. Вектор Пойнтинга П также направлен по радиусу. Угол между ними равен нулю (рис. 25:3). Элемент сферической

поверхности можно рассматривать как криво­линейный квадрат, площадь его (рис. 25.3):

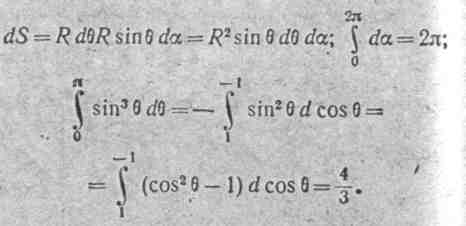
Заменим Р_т на 2I² (I — действующее значение тока). В результате окажется, что поток вектора Пойнтинга через сферическую поверхность радиусом R, представляющий собой мощность P_s, излученную элементом тока, не зависит от радиуса и равен:

Величину R_s называют сопротивлением излучения. Чем больше
R_s, тем больше излученная мощность при том же I. Сопротивле­ние излучения прямо пропорционально квадрату длины излучателя
и, что особенно важно, обратно пропорционально квадрату длины
волны λ

Так как длина волны λ == vlf, то излученная мощность прямо пропорциональна квадрату частоты. Если частота мала, например всего 50 Гц, то излучения практически нет. При радиочастоте излу­чение значительно. Например, при частоте 50 10⁶ Гц излучение больше, чем при частоте 50 Гц, в 10¹² раз.

Пример 225. По отрезку линейного провода длиной dl =3 см протекает переменный ток I= 0,2 А. Частота тока f = 10⁹ Гц. Найти сопротивление и.мощность излучения.

 

§ 25.5. Понятие об излучающем диполе. При выводе формул § 25.4 в качестве излучателя электромагнитной энергии, был взят небольшой отрезок провода, по которому протекал синусоидальный ток. Но точно такие же формулы были бы получены, если бы вместо элемента тока был взят излучающий диполь. Под излучающим диполем понимают отрезок линейного провода с сосредоточенными на концах его емкостями в виде шаров (рис. 25.4, а).

Полагают, что длина диполя l много меньше длины волны λи сечение провода ничтожно мало: При этих условиях распределенную

емкость самого проводника в первом приближении можно не принимать во внимание и учитывать только емкости шаров.

На рис. 25.4, б показана схема, в которой генератор синусоидального напряжения высокой частоты через коаксиальный кабель присоединен к двум вертикально располо-

женным проводникам (изображены «жирными» линиями), соединенным в свою очередь с двумя шарами (шариками) диполя. Под воздействием напряжения генератора шарики диполя периодически перезаряжаются. Положим, что заряд верхнего шарика q изменяется по закону — Q_m cos ωt, а заряд нижнего шарика — по закону Q_m cos ωt: Тогда по вертикальным проводникам при периодической перезарядке шариков будет протекать ток проводимости:

Этот ток замыкается через диэлектрик в виде тока смещения, как показано на рис. 25.4, б.

Важно обратить внимание на то, что по двум вертикальным про-

водникам длиной l/2 каждый при периодической перезарядке шари-

ков протекает ток проводимости i, т. е. два вертикальных проводника

длиной l/2 (или ) с током i, которыми соединены шарики диполя,

представляют собой элемент тока i dl (или i dl), о котором шла речь в § 25.4..

Посредине элемента тока на рис 21.4, б есть разрыв, а в элементе тока (рис. 25.1) разрыва нет. Но это не имеет существенного значения, так как разрыв может быть весьма малым по сравнению с длиной i(dl).

 

Таким образом, все выводы § 25.4, сделанные по отношению к эле­менту тока idl, применимы и к излучателю в виде диполя, т. ё. к из­лучателю, составленному двумя периодически перезаряжающимися шариками, соединенными тонким проводником.

§ 25.6. Дополнительный анализ поля излучения. Как уже го­ворилось в § 25.4, в ближней зоне излучателя основную роль играют составляющие напряженности электрического поля Е_θ и E_R, обратно пропорциональные третьей степени расстояния рассматриваемой точки до излучателя.

Эти составляющие на 90° отстают по фазе от протекающего по проводнику тока или, другими словами, по фазе совпадают с зарядом одного из шаров излучающего диполя.

Из предыдущего [см. формулы (19.74), (19.75)] известно, что на­пряженность электрического поля, созданного диполем, заряды которого неизменны во времени, также обратно пропорциональ­на третьей степени расстояния рассматриваемой точки до центра диполя.

Следовательно, для определения мгновенного значения напря­-
женности электрического поля излучающего диполя в ближней зоне
практически можно пользоваться формулами, вытекающими из за­
кона Кулона. В свою очередь, напряженность магнитного поля в ближ­-
ней зоне излучателя [см. формулу (25.37)] обратно пропорциональна
квадрату расстояния рассматриваемой точки до элемента тока и по
фазе совпадает с током

Из закона Био — Савара — Лапласа [см. формулу (21.36)] следует, что напряженность магнитного поля, создаваемого элементом постоян­ного тока, также обратно пропорциональна квадрату расстояния рас­сматриваемой точки до элемента тока.

На основании этого можно сделать вывод, что в ближней зоне (при R λ ) для определения мгновенного значения напряженности магнитного поля практически можно пользоваться формулой Био — Савара — Лапласа. Применимость формул, описывающих статиче­ские поля, для подсчета мгновенных значений Е и Н переменных полей в ближней зоне (при R λ), объясняется тем, что в ближней зоне можно пренебречь запаздыванием.

Границы ближней зоны зависят от частоты. Так, например, при f = 50 Гц λ= 6 10⁶ м; при f = 10¹⁰ Гц λ= 3 см. Следовательно, при частоте 50 Гц законами Кулона и Био - Савара— Лапласа прак­тически можно пользоваться при любом расстоянии точки до элемента тока или диполя. Совершенно иная картина будет при частоте 10¹⁰ Гц. В этом случае границы ближней зоны удалены от излучателя всего на доли сантиметра и все пространство вокруг него следует рассмат­ривать как дальнюю зону. В дальней зоне «кулонова» составляющая напряженности электрического поля ничтожно мала по сравнению с волновой составляющей Е, а «био — саварова» составляющая напряженности магнитного поля ничтожно мала по сравнению с вол­новой составляющей Н.

 

 

 

 

B ближней зоне поток вектора Пойнтинга имеет две составляющие: первая изменяется во времени по закону sin 2ωt или cos 2ωt; вторая — пo закону sin² ωt или cos² ωt.

При подсчете потока вектора Пойнтинга через сферическую поверхность радиусом R в ближней зоне за период переменного тока доказывается, что поток от первой составляющей равен нулю, поскольку Переднее за период значение функции sin 2ωt или cos 2ωt равно нулю; поток от второй составляющей отличен от нуля. Физически это озна­чает, что в ближней зоне происходит два качественно различных в энергетическом отношении процесса.

Первый процесс — это процесс периодического обмена энергией между источником энергии, к которому присоединен излучатель, и ближней зоной. Энергия то забирается от источника и накапливается в электромагнитном поле ближней зоной, то отдается обратно источнику. Этот процесс характерен для «кулонова» и «био ^:—саварова» полей ближней зоны.

Второй процесс — это процесс излучения энергии. Он характери­зует волновой процесс в ближней зоне. Излученная энергия состав­ляет относительно небольшую величину по сравнению с энергией, периодически накапливаемой в электромагнитном поле ближней зоны и затем отдаваемой источнику питания.

От излучателя в пространство распространяются электромагнитные волны*. Эти волны для фиксированного момента времени схематически можно представить рис. 25.5, а. На нем линии Е образуют замкнутые фигуры, лежащие в меридиональных плоскостях. Линии Е

Существование электромагнитных волн экспериментально было доказано Г.Герцем в 1887—1888 гг. Справедливость электромагнитной теории света была подтверждена опытами П.Н. Лебедева, в 1895 г., который измерил световое давление, теоретически предсказанное Д. Максвеллом.

А. С. Поповым 7 мая 1895 г. на заседании Русского физико-химического общества был прочитан доклад об успешно проведенных опытах по приему и передаче радиосигналов. Поэтому 7 мая отмечают как День радио.

 

 

охвачены линиями Н, которые представляют собой окружности с цент­ром на оси элемента тока. Чтобы не загромождать рис. 25.5, а, на нем изображены всего две линии Е и две линии Н.

Линии напряженности электрического поля в меридиональной пло­скости для волновой зоны излучателя при различных моментах вре­мени представлены на рис. 25.5,6, где изображена также кривая изменения заряда излучающего диполя в функции времени. Чем больше по абсолютной величине становятся заряды диполя, тем большее количество линий Е начинается или соответственно оканчивается на них.

По мере распространения электромагнитной волны в окружающее пространство форма линий Е непрерывно меняется. Когда заряды диполя по абсолютной величине начинают уменьшаться, начинает уменьшаться и число исходящих из них линий Е. При этом образуются замкнутые на себя линии Е. Пакет замкнутых на себя линий Е сцеплен с пронизывающими этот пакет линиями Н (см. рис. 25.5, а). В сле­дующий полупериод, когда заряды шаров меняют знаки на противо­положные, образуется аналогичный пакет замкнутых на себя линий Е,

отличающийся от предыдущего лишь направлением вихря Е.

§ 25.7. Расчет поля реальных излучателей. Практически в ка­честве излучателей используют антенны. Простейшая антенна пред­ставляет собой отрезок провода длиной l, расположенный вертикально по отношению к поверхности земли (рис. 25.6, а). Генератор высокой частоты включают между антенной и землей. За счет наличия распределенных емкостей антенны и проходящих через них токов сме­щения, ток по высоте антенны меняется по амплитуде и фазе (см. эпюру изменения амплитуд на рис. 25.6, а). Антенна обладает высокой спо­собностью к излучению вследствие того, что создаваемые ею электри­ческое и магнитное поля распределены в одной и той же области пространства, окружающего антенну (см, рис. 25.6, а).

Влияние земли на поле учитывают, вводя в расчет зеркальное изображение антенны (полагая, что земля является идеальным про­водником). При этом длина антенны оказывается равной 2 l, а эпюра тока дополняется второй половиной (рис. 25.6, б)*. Для расчета поля,

-------------------------------

* Мощность, излученная в пространство над землей таким излучателем, равна половине мощности излучателя удвоенной длины с током i.

 

создваемого антенной, ее заменяют совокупностью малых отрезков длиной dl, на каждом из которых ток принимают неизменным по амплитуде и фазе. Тогда напряженность поля в произвольной точке пространства можно найти как геометрическую сумму напряженностей создаваемых всеми малыми отрезками антенны.

Для увеличения емкости антенны, а следовательно, и проходящего по ней тока при том же напряжении генератора антенну часто дополняют горизонтальным участком (рис. 25.6, в).

§ 25.8. Излучение магнитного диполя и принцип двойственности. В § 19.11 и 25.5 шла речь об электрическом диполе, обладающем электрическим моментом р_э= q_э l. В теории поля пользуются также понятием магнитного диполя. Магнитный диполь образован двумя магнитными зарядами q_м и — q_м расположенными на рас­стоянии l. Диполь обладает магнитным моментом p_м = q_м l (рис. 25.7, а).

Из § 14.24 известно, что виток (рамка) с током i, охватывающим площадь S,также обладает магнитным моментом р_м = iS (рис. 25.7, б). Магнитный диполь можно рассматривать как расчетный эквивалент витка с током, если равны их магнитные моменты, т. е. если q_мl = iS. Изменение тока в рамке соответствует изменению магнитных зарядов диполя во времени и протеканию между ними «магнитного тока смещения». Излучение энергии рамкой стоком в расчетном смысле можно представить как излучение магнитного диполя.
Если обратиться к уравнениям Максвелла rot Н = ε_а dЕ/dt и rotЕ=—μ_а dH/dt, но нетрудно заметить, что первое уравнение получается из второго, а второе — из первого, если заменить Н на Е, а ε_а на —μ_а. Это свойство уравнений Максвелла, называют принципом двойственности. Его применяют для решения задач электродинамики, двойственных уже решенным.Так, имея решение для поля, создаваемого электрическим диполем, получают решение для поля, создаваемого магнитным диполем, т. е. рамкой с синусоидально вменяющимся током (считая, что оси R, α, θ расположены в соответствии с рис. 25.1). Так как в случае электрического диполя i=dq/dt, то при i — I_m sin ωt: I_m == jωq_m, а I_md l=jωq_mdl=jωp. Подставив в (25.38) jωpвместо l_mdl_t запишем формулу для напряженности магнитного поля в дальней зоне, через электрический момент диполя р:

. § 259. Переход плоской электромагнитной волны из одной среды в другую. Рассмотрим условия перехода плоской синусоидаль­но изменяющейся электромагнитной волны из первой среды с волновым сопротивлением Z_{B l} во вторую среду с волновым сопротивлением Z_B2. Примем, что волна падает перпендикулярно границе раздела сред (рис. 25.7, в). Волна частично пройдет во вторую среду, частично от­разится.

В первой среде будут падающая (индекс «п») и отраженная (индекс
«о») волны, во второй— только падающая (поэтому индекс «п» у нее
не будем ставить). Падающую во второй среде волну называют также
преломленной.

Для удобства чтения рис. 25.7, в векторы,, характеризующие падающую и отраженную волны в первой среде, смещены по вертикали и несколько отодвинуты от границы раздела сред. На границе раздела сред должны быть равны тангенциальные составляющие напряжен­ности электрического поля и тангенциальные составляющие напря­женности магнитного поля:

Ё_1п + Ё_1о=Ё₂; (25.43)

Н_1n + Н₁₀ = Н₂. (25.44)

Уравнения (25.43) и (25.44) полностью тождественны уравнениям, которыми связаны напряжения и токи падающей, отраженной и.пре-. ломленной волн при переходе волны с одной линии с распределенными параметрами на другую (см. § 12.6).

Комплекс напряженности электрического поля Е_1п равен ком­плексу напряженности магнитного поля Н_1п, умноженному на Z_Bl:

Е _1Π ⁼⁼ Н_1Π Z_B1.

Для отраженной волны в соответствии, с изменением направления Движения энергии на противоположное: Е_1о = — Н_1о Z_B1

Для преломленной волны Ё₂ = H₂Z_B2

Из уравнений (25.43) и (25.44) с учетом предыдущих строчек получим

 

Проанализируем полученные результаты. Значения Ё_1о, Н_1о и Е₂, Н₂ зависят от соотношения между волновыми сопротивлениями обеих сред. Наибольший практический интерес представляет случай, когда волна падает из воздуха на поверхность металла. В этом случае первой средой является воздух, а второй — металл. Так как волновое сопротивление проводящей среды зависит не только от ее проводимости и «магнитной проницаемости, но и от частоты [см. формулу (23.12)], то для определенности положим, что проводящей средой является медь, а частота f = 10⁸ Гц. Сопоставим значения волновых сопротивлений для диэлектрика и для металла (см. формулы для Z_B на стр. 150 и 136). Для воздуха Z_Bl = 377 Ом. Для меди (v = 5,6 10⁷ Ом^-1 м-¹) при f=10⁸ Гц, Z_B2 = 0,00357еⁱ⁴⁵° Ом. Если подставить значения Z_B1 и Z_B2 в (25.47), то получим Ё_{1о 1П}; Н_1о Н_1п, т. е..от по­верхности металла электромагнитная волна почти полностью отра­жается с переменой знака у напряженности электрического поля. Ta часть волны, которая все же проникнет в металл, быстро в нем «затухнет. Если бы проводящая среда имела γ, стремящуюся к бесконечности, то тогда она являлась бы идеальным зеркалом для электромагнитной волны.

Явление отражения электромагнитных волн от проводящих сред лежит в основе радиолокации.
В более общем случае электромагнитная волна, распространяясь из среды 1 в среду 2, направлена не перпендикулярно границе раздела сред (рис. 25.7, г).
В среде 1:

отсутствует). Этот режим используется, например, в оптических волноводах. Если α+ V = 90° — возникает полное преломление, когда отраженная волна отсутствует.

В заключение упомянем о явлении дифракции. Дифракцией называют явление отражения и преломления электромагнитных волн от проводящего или диэлектрического тела, а также изменение структуры и направления волн при прохождении их через отверстие (щель) в каком-либо теле, например в.пластинке, когда размеры тела или щели соизмеримы с длиной электромагнитной волны.

Качественно рассмотрим, как влияет на поле плоской волны помещенный в это поле длинный цилиндр радиуса а, полагая, что ось цилиндра расположена перпендикулярно вектору Пойнтйнга падающей волны, а ее вектор Е парал­лелен оси цилиндра.

Рассмотрим три характерных случая. I. Если длина вол­ны λ , то действуют законы геометрической оптики и за цилиндром будет область тени — рис. 25.8, а. 2. Если вне и внутри цилиндра λ а, то можно пренебречь запаздыванием, и тогда поля Е и Н внутри и вне цилиндра определяются в условиях, близких к статическим. 3. Если λ/а а эта случай, наиболее типичный для дифракционных за-

дач, то в области за цилиндром, где на рис. 25.8, а была тень, появляется интенсив­ное поле. На рис. 25.8, б изображена эпюра для. напряженности Н рассеянного поля, когда проводимость у цилиндра стремится к бесконечности. Физически интенсивное! поле вместо тени получается за счет того, что наводимые в верхней части проводящего цилиндра токи затекают в нижнюю его часть и там служат излучателем (вторичным источником поля). Наличие мелких углублений на диаграмме объясняется интерференцией волн.

Вопросы для самопроверки

1. Как связан исток вектора А с потенциалом φ? 2. Почему первое слагаемое правой части