ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ

РЕШЕНИЕ ЗАДАЧ ПО АЛГЕБРЕ

ДЛЯ 3 КУРСА ОЗО

ФАКУЛЬТЕТА МАТЕМАТИКИ

И ИНФОРМАТИКИ

 

 

Тула 2000

Рецензент -

канд. физ.-мат. наук, доцент, зав. кафедрой математического анализа

ТГПУ им. Л. Н. Толстого И. В. Денисов

 

Решение задач по алгебре для 3 курса ОЗО факультета математики и информатики

Методические рекомендации предназначены для студентов 3 курса ОЗО факультета математики и информатики. Приведены основные теоретические сведения, необходимые для решения задач. Разобраны решения типовых заданий. Приведены упражнения для решения на практических занятиях. Даны задания для контрольных работ.

 

Составитель -

канд. физ.-мат. наук, доцент кафедры алгебры и геометрии ТГПУ им. Л. Н. Толстого

Ю. А. Игнатов

 

© Ю. Игнатов, 2000 г.

РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ

Целое число a называется кратным числу b, или a делится на b, что записывается в виде a M b, если существует такое целое число c, что a = bc. В этом случае b называется делителем a, что записывается в виде b ï a.

Целое число p называется простым, если оно отлично от ±1 и не имеет делителей, отличных от ±1, ± p.

Целое число a называется составным, если оно может быть разложено в произведение двух целых чисел, отличных от 0, ±1.

Каноническим разложением числа a на простые множители называется представление его в виде

,

где e = ±1, p₁, …, p_k - различные простые числа, a₁, …, a_k > 0.

Теорема 1. Составное натуральное число a имеет простой делитель, не превосходящий .

П р и м е р 1.1. Разложить на простые множители числа: а) 919; б) 833.

Р е ш е н и е. а) Имеем = 30, … Выписываем все простые числа, не превосходящие 30: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Для каждого из них проверяем, является ли оно делителем числа 919. Убеждаемся, что 919 не делится ни на одно из этих чисел, значит, по теореме 1 является простым.

б) Имеем = 28,… Выписываем все простые числа, не превосходящие 28: 2, 3, 5, 7, 11, 13, 17, 19, 23. Проверяя их по порядку, получаем 833 = 7×119. Далее находим = 10,… Поэтому нам осталось проверить на делимость числа, не превосходящие 10. При этом начинать надо с 7, так как на предыдущие числа 119 делиться не может. Следовательно, остается проверить одно число 7. Убеждаемся, что 119 = 7×17. В итоге получаем разложение 833 =7²×19.

Упражнение 1.1. Разложите на простые множители числа 831; 781; 1331; 703.

НОД и НОК

Наибольшим общим делителем целых чисел a₁, …, a_k называется такой их общий делитель, который кратен любому их общему делителю.

Наибольший общий делитель чисел a₁, …, a_k обозначается НОД(a₁, …, a_k) или (a₁, …, a_k). Он определяется с точностью до знака.

Если (a₁, …, a_k) = d, то существует линейное представление

d = x₁a₁+ … +x_k a_k ,

где x₁,… x_k - некоторые целые числа.

Для нахождения НОД двух целых чисел и его линейного представления используется алгоритм Евклида, основанный на следующих теоремах.

Теорема 2.1 (о делении с остатком). Для любых двух целых чисел a и b, где b > 0, существует единственная пара q, r, такая что

a = bq + r, 0 £ r < b.

Теорема 2.2. Если a = bq + r, то (a, b) = (b, r).

Пример 2.1. Найти НОД(75, 27) и его линейное представление.

Решение. Строим цепочку делений с остатком. Для этого делим с остатком первое число на второе, затем делитель на получившийся остаток, и так далее, пока не получим нулевой остаток. Последний ненулевой остаток и есть искомый НОД.

75 = 27×2 + 21;

27 = 21×1 + 6;

21 = 6×3 + 3;

6 = 3×2.

Следовательно, НОД(75, 27) = 3.

Для нахождения линейного представления выражаем НОД из предпоследней строки, в которой он появился как остаток. Далее в получившееся выражение последовательно подставляем выражения для остатков, получившихся в предыдущих строках, двигаясь снизу вверх:

3 = 21 – 6×3 = 21 – (27 – 21)×3 = 21×4 – 27×3 = (75 – 27×2)×4 – 27×3= 75×4 – 27×11.

Итак, НОД(75, 27) = 3 = 75×4 – 27×11.

Упражнение 2.1. Найдите НОД и его линейное представление: (124, 168); (215, 95).

 

ЦЕПНЫЕ ДРОБИ

Цепной, или непрерывной дробью называется выражение вида

,

где a ₀ – целое, a ₁, …, a _n – натуральные, a _n > 1. Для компактности цепную дробь записывают в виде [ a ₀; a ₁, …, a _n].

Пример 3.1. Записать в виде цепной дроби число .

Решение. Коэффициенты цепной дроби – это частные, получающиеся в цепочке делений с остатком, организованной по алгоритму Евклида:

48 = 13×3 + 9;

13 = 9×1 + 4;

9 = 4×2 + 1;

4 = 1×4.

В итоге получаем = [3; 1, 2, 4].

Упражнение 3.1. Запишите в виде цепной дроби число

k-ой подходящей дробью к цепной дроби A = [ a ₀; a ₁, …, a _n] называется цепная дробь A _k = [ a ₀; a ₁, …, a _k], где 0 £ k £ n.

Определим индуктивно числа P_k, Q_k, k = 0, 1, …, n:

P ₀ = a ₀,

P ₁ = a ₀ a ₁ + 1,

P _i+1 = P _i a _i+1 + P _{i –1} , i = 1,…, k–1;

Q ₀ = 1,

Q ₁ = a ₁,

Q _i+1 = Q _i a _i+1 + Q _{i –1} , i = 1,…, k–1.

Теорема 3.1. Для любой подходящей дроби A _k, k = 0, 1, …, n, к цепной дроби A = [ a ₀; a ₁, …, a _n] имеет место равенство .

Пример 3.2. Свернуть цепную дробь A = [2; 3, 1, 3].

Решение. Для нахождения числителей и знаменателей подходящих дробей строим таблицу:

i
a i
P i		2×3 + 1 = 7	7×1 + 2 = 9	9×3 + 7 = 34
Q i			3×1 + 1 = 4	4×3 + 3 = 15

Таким образом, A = .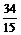

Упражнение 3.2. Сверните цепную дробь: [3; 3, 2, 2]; [0; 2, 1, 4, 3].

ПОЗИЦИОННЫЕ СИСТЕМЫСЧИСЛЕНИЯ

В десятичной системе счисления число в развернутом виде записывается как = a_k ×10 ^k + a_k-1 ×10 ^k-1 + … + a ₀. Значение числа определяется не только значением его цифр a_k ×, a_k-1, …, a ₀, но и местом, позицией, которые они занимают в числе. Аналогично в произвольной m-ичной системе имеем

= a_k ×m ^k + a_k-1 ×m ^{k- 1}+ … + a ₀. (1)

Черта над числом означает, что a_k ×, a_k-1, …, a ₀ являются цифрами числа, а не множителями в произведении. Основание системы m обозначается в виде индекса.

Формула (1) позволяет перевести число из m-ичной системы в десятичную. Для этого ее преобразовывают к более удобному для вычислений виду:

= a_k ×m ^k + a_{k- 1}×m ^{k- 1}+ … + a ₀ = (…(a_k ×m + a_{k- 1})×m + … a ₁)m+ a ₀.

Пример 4.1. Перевести число 5214₇ в десятичную систему.

Решение. Имеем

5214₇ = ((5×7 + 2)×7 + 1)×7 + 4 = 1824.

Для перевода числа из десятичной системы в m-ичную пользуемся тем, что при делении числа 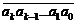, записанного в m-ичной системе, на m получаем в частном и в остатке a ₀. Это позволяет последовательно определить все цифры числа, начиная с последнего.

Пример 4.2. Перевести число 3257₁₀ в 8-ричную систему.

Решение. Имеем

3257 = 407×8 + 1;

407 = 50×8 + 7;

50 = 6×8 + 2.

Следовательно, 3257₁₀ = 6271₈.

Упражнение 4.1. Переведите число из одной системы в другую: 364_7®10; 2032_5®10; 349_10®6; 143_10®12; 1604_8®6.

Для перевода из m-ичной системы в n-ичную число предварительно переводим в десятичную систему. Но если одно из чисел m, n есть степень другого, то перевод упрощается. Например, для перевода из двоичной системы в четверичную и восьмеричную или обратно используем таблицы перевода цифр:

 

2-ичная	8-ричная

 

2-ичная	4-ричная

 

 

Пример 4.3. Осуществить перевод 305_8®2, 1001011_2®4.

Решение. Пользуясь первой таблицей, осуществляем перевод из 8-ричной в двоичную систему по цифрам:

305₈ = 011000101₂ = 11000101₂.

Для осуществления перехода из двоичной системы в 4-ричную цифры числа в двоичной системе разбиваем на пары, начиная справа, дописав при необходимости слева 0. Каждую пару переводим в 4-ричную цифру с помощью второй таблицы:

1001011₂ = 01¢00¢10¢11 = 1023₄.

Упражнение 4.2. Переведите число из одной системы в другую: 230_4®2; 101101011_2®8; 1203_4®8; 150_8®4.

ФУНКЦИЯ ЭЙЛЕРА

Функцией Эйлера от натурального числа n называется число j(n) натуральных чисел, не превосходящих n и взаимно простых с n.

Функция Эйлера мультипликативна: если (m, n) = 1, то j(mn) = j(m) j(n).

Для вычисления функции Эйлера j(n) используем каноническое разложение числа n на простые множители. Имеем

j() = .

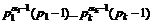В частности, j(p) = p – 1, j(p^k) = p^k-1 (p – 1).

Пример 5.1. Вычислить функцию Эйлера от чисел 47; 72.

Решение. Имеем j(47) = 46; j(72) = j(2³×3²) = 2²(2 – 1)×3¹(3 – 1) = 24.

Упражнение 5.1. Вычислите j(125), j(97), j(136), j(216).

Упражнение 5.2. Сколько натуральных чисел в промежутке от 1 до 120, не взаимно простых с 30?

Упражнение 5.3. Решите уравнения j(5 ^x) = 100; j(7 ^x) = 294;

j(3 ^x ×5 ^y) = 600.

Упражнение 5.4. Докажите, что при m ³ 3 значение j(m) – число четное.

Упражнение 5.5. Решите уравнения j(x) = 2; j(x) = 4.

СРАВНЕНИЯ

Числа a и b называются сравнимыми по модулю m, это записывается в виде a º b (mod m), если a и b имеют одинаковые остатки при делении на m. Это равносильно условию (a – b)M m.

Свойства сравнений:

1. a º b (mod m), c º d (mod m) Þ a ± c º b ± d (mod m);

2. a º b (mod m), c º d (mod m) Þ ac º bd (mod m);

3. ac º bc (mod mc) Þ a º b (mod m);

4. ac º bc (mod m), (c, m) = 1 Þ a º b (mod m).

Пример 6.1. Найти последнюю цифру числа 27³⁹.

Решение. Число сравнимо со своей последней цифрой по mod 10. Поэтому, пользуясь свойствами сравнений, имеем 27_­³⁹º 7_­³⁹(mod 10). Далее находим 7² º 9, 7³ º 3, 7⁴ º 1(mod 10). Поэтому

7³⁹ = 7^4×9+3 = (7⁴)⁹×7³ º 1⁹×3 º 3 (mod 10).

Последняя цифра числа есть 3.

Упражнение 6.1. Найдите последнюю цифру числа 23⁵³; 42³⁵; .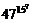

Отношение сравнения по модулю m есть отношение эквивалентности. Числа, сравнимые по модулю m, образуют класс эквивалентности, называемый классом вычетов по модулю m. Число различных классов вычетов по модулю m равно m.

Полной системой вычетов по модулю m называется система представителей, взятых по одному из каждого класса вычетов по модулю m.

Упражнение 6.2. Образуют ли числа: а)17, 21, 120, 34, 58; б) 27, 12, 53, 28, 44, 77 полную систему вычетов по какому-нибудь модулю?

Согласно теореме 2.2 все числа из одного класса вычетов по модулю m имеют один и тот же НОД с модулем m. Поэтому если одно число из класса вычетов взаимно просто с модулем, то все числа из этого класса будут взаимно просты с модулем. Такой класс вычетов называется взаимно простым с модулем.

Приведенной системой вычетов по модулю m называется система представителей, взятых по одному из каждого класса вычетов, взаимно простого с m.

Приведенная система вычетов по модулю m содержит j(m) элементов.

Теорема 6.1 (Эйлер). Если (a, m) = 1, то a^j(m) º 1(mod m).

Теорема 6.2 (Ферма). Если p – простое, a не делится на p, то a^p-1 º 1(mod p).

Пример 6.2. Найти две последних цифры числа 233⁸⁹.

Решение. Чтобы найти две последних цифры числа, следует рассматривать сравнение по модулю 100. Имеем (233, 100) = 1, j(100) = 40, и по теореме Эйлера 233⁴⁰º 1(mod 100). Поэтому

233⁸⁹ º 233^40×2+9º (233⁴⁰)²×233⁹º 233⁹º 33⁹ (mod 100).

Далее вычисляем

33² = 1089 º 89 (mod 100);

33⁴ = (33²)² º 89² = 7921 º 21(mod 100);

33⁸ = (33⁴)² º 21² = 441 º 41(mod 100);

33⁹ = 33⁸×33 º 41×33 = 1353 º 53(mod 100).

Значит, наше число оканчивается на 53.

Упражнение 6.3. Докажите, что:

а) a ¹² – 1 M 7, если (а, 7) = 1;

б) a ¹² – b ¹² M 65, если (а, 65) = (b, 65) = 1;

в) а ⁵⁶¹ º а (mod 11).

РЕШЕНИЕ СРАВНЕНИЙ

Если число х ₀ удовлетворяет сравнению

a ₀ x ⁿ + a ₁ x ^n-1 + … + a _n º 0 (mod m), (1)

то этому сравнению удовлетворяют все числа, сравнимые с х ₀ по модулю m. Поэтому решением сравнения считается класс вычетов по модулю m, содержащий х ₀.

Так как классов вычетов конечное число, то сравнение (1) всегда можно решить полным перебором, проверив какую-нибудь полную систему вычетов по модулю m.

Сравнение первой степени

ax º b (mod m) (2)

при (a, m) = 1 имеет единственное решение. При небольших а его можно решить преобразованием коэффициентов: число b заменяется на сравнимое с ним по модулю m, прибавлением или вычитанием кратного m. Цель этого – получить число, делящееся на а. Затем производится сокращение.

Пример 7.1. Решить сравнение 3 х º 7 (mod 17).

Решение. Так как (3, 17) = 1, то сравнение имеет единственное решение. Преобразуем сравнение и получаем решение:

3 х º 24 (mod 17);

х º 8 (mod 17).

При больших а этот метод оказывается неэффективным. В этом случае для решения сравнения (2) разлагаем число в цепную дробь. Находим числители подходящих дробей к этому числу. Пусть P_{k -1} – предпоследний числитель. Тогда решение сравнения находится по формуле

x º (-1) ^k P_{k -1} b (mod m). (3)

Пример 7.2. Решить сравнение 31 х º 17 (mod 42).

Решение. Так как (31, 42) = 1, то сравнение имеет единственное решение. Разлагая число в цепную дробь как показано в разделе 3, получаем = [1; 2, 1, 4, 2]. Находим числители подходящих дробей:

 

i
ai
P i

Подставляя в формулу (3), получаем

x º (-1)⁴×19×17 º 323 º 29 (mod 42).

Если (a, m) = d >1, то сравнение (2) не имеет решений при d не делящем b. Если b M d, то сравнение имеет d решений. Для их нахождения сокращаем обе части и модуль сравнения на d и приходим к сравнению a ₁ x º b ₁ (mod m ₁), которое согласно предыдущему имеет единственное решение x º x ₀(mod m ₁). Тогда решения исходного сравнения находим по формулам

x º x ₀, x ₀ + m ₁, x ₀ + 2 m ₁, …, x ₀ + (d – 1) m ₁ (mod m).

Пример 7.3. Решить сравнение 12 х º 15 (mod 33).

Решение. Имеем (12, 33) = 3. Так как 15M3, то сравнение имеет 3 решения. Сократив на 3, получаем сравнение 4 х º 5 (mod 11), которое решим методом преобразования коэффициентов:

4 х º 16 (mod 11);

х º 4 (mod 11).

Следовательно, сравнение имеет решения х º 4, 15, 26 (mod 33).

Упражнение 7.1. Решите сравнения:

а) 4 х º 11 (mod 23);

б) 5 х º 3 (mod 14);

в) 8 х º 19 (mod 15);

г) 41 х º 21 (mod 53);

д) 34 х º 19 (mod 39);

е) 10 х º 13 (mod 24);

ж) 15 х º 24 (mod 36);

з) 12 х º 22 (mod 40);

и) 16 х º 20 (mod 36).