РЕШЕНИЕ ЗАДАЧ ПО АЛГЕБРЕ
ДЛЯ 4 КУРСА ОЗО
ФАКУЛЬТЕТА МАТЕМАТИКИ
И ИНФОРМАТИКИ
Тула 2001
Решение задач по алгебре для 4 курса ОЗО факультета математики и информатики
Методические рекомендации предназначены для студентов 4 курса ОЗО факультета математики и информатики, изучающих теорию многочленов в курсе алгебры. Приведены основные теоретические сведения, необходимые для решения задач. Разобраны решения типовых заданий. Приведены упражнения для решения на практических занятиях. Даны задания для контрольных работ.
Составитель -
канд. физ.-мат. наук, доцент кафедры алгебры и геометрии ТГПУ им. Л. Н. Толстого
Ю. А. Игнатов
Рецензент -
канд. физ.-мат. наук, доцент, зав. кафедрой математического анализа
ТГПУ им. Л. Н. Толстого И. В. Денисов
Учебное издание
Решение задач по алгебре для 4 курса ОЗО факультета математики и информатики
Составитель
ИГНАТОВ Юрий Александрович
Формат 60 ´ 84 / 16. Бумага офс.
Усл. печ. л. 0,93. Уч.-изд. л. 1,4. Тираж 120 экз. Изд. № 35.
© Ю. Игнатов, 2001 г.
ТЕОРИЯ МНОГОЧЛЕНОВ
Деление с остатком. Схема Горнера
Многочленом над полем F называется формальное выражение
f = a 0 + a 1 x + … + anxn, где a 0, a 1, … an Î F, an ¹ 0.
Степенью многочлена называется число deg f = n в этом выражении. Степень многочлена f = 0 не определена. Многочлен нулевой степени – это ненулевой элемент поля F. Над многочленами естественным образом определены операции сложения, вычитания, умножения, относительно которых множество многочленов образует кольцо, обозначаемое F[ x ]. Имеет место теорема о делении с остатком:
Теорема 1.1. Для многочленов f, g Î F[ x ], g ¹ 0, существует, и при том единственная, пара многочленов q, r, такая что
f = gq + r, deg r < deg g или r = 0.
Теорема 1.2 (Безу). Остаток от деления многочлена f на двучлен х – с равен f (с).
Для практического выполнения деления с остатком используется деление «уголком», как для чисел. При этом многочлены записываем в порядке убывания степеней членов. Для нахождения очередного члена в частном старший член очередного остатка делим на старший член делителя.
Пример 1.1. Разделить 2 х4 – 4 х3 + 3 х + 4 с остатком на 2 х2 – х + 1.
Решение.
Таким образом, 2 х 4 – 4 х 3 + 3 х + 4 = (2 х 2 – х + 1)(х 2 – 2 х – 3/2) + (-13/2 х + 11/2).
Для деления многочлена f (x) на двучлен вида х – с применяется более простой способ, основанный на схеме Горнера. Она оформляется в виде таблицы. В первой строке расставляем коэффициенты многочлена в порядке убывания степеней. Эта строка подчеркивается. В левом столбце второй строки ставим число с. Следующий элемент второй строки сносится из подчеркнутой строки. А в каждом следующем столбце элемент получается умножением только что полученного элемента на с и прибавлением подчеркнутого элемента из своего столбца. В результате последний полученный элемент есть f (с), то есть остаток от деления многочлена f (x) на х – с, а остальные элементы – коэффициенты частного.
Пример 1.2. Разделить 3 х 4 – 5 х 3 + х + 3с остатком на х – 2.
Решение.
| -5 | |||||
| 3×2 – 5 = 1 | 1×2 + 0 = 2 | 2×2 + 1 = 5 | 5×2 + 3 = 13 |
Таким образом, 3 х 4 – 5 х 3 + х + 3= (х – 2)(3 х 3 + х 2 + 2 х + 5) + 13.
Этот способ применяется и для нахождения значения f (с). Если требуется найти несколько значений для различных с, то каждому соответствует своя строка. При этом должны быть подчеркнуты только коэффициенты многочлена, остальные строки не подчеркиваются. Если же потребуется перейти к другому многочлену, являющемуся частным при одном из делений, то его коэффициенты следует подчеркнуть и продолжать работать с ними.
Пример 1.3. Разложить многочлен х 4 – 2 х 3 + 3 х 2 + 1по степеням х – 1.
Решение. Для выполнения этой задачи следует разделить с остатком на х – 1 исходный многочлен, затем получившееся частное, и так далее до конца. Оформляем это в виде схемы Горнера.
| -2 | |||||
| -1 | |||||
Искомое разложение имеет вид
f = (х – 1)4 + 2(х – 1)3 + 3(х – 1)2 + 4(х – 1) + 3.
Элемент с называется корнем многочлена f, если f (с) = 0. Корень с имеет кратность k, если f = (x – c) kg, причем g (с) ¹ 0.
Упражнения.
1.1. Разделите с остатком:
а) х 5 + 3 х 4 – 2 х 3 – 4 х + 3 на х 2 – 3 х + 2;
б) 2 х 4 – 2 х 3 + х 2 – 3 х + 1 на 2 х 2 – х + 3.
1.2. Найдите остаток от деления:
а) х 17 + 2 х 14 – 5 х 6 – х 2 + 2 на х – 1;
б) х 27 – 3 х 15 + 4 х 4 – 3 х 3 + 1 на х 2 – 1;
в) х 20 – 2 х 11 + х 6 + 3 х 4 + 3 на х 2 + х – 2.
1.3. При делении многочлена f (x) на х – 1 и х – 2 остатки равны соответственно 1 и 2. Найдите остаток от деления f (x) на произведение (х –1)(х –2).
1.4. Разложите f (x) по степеням x – c:
а) f (x) = 2 х 4 – 4 х 3 – 2 х 2 + х + 3, с = 2;
б) f (x) = х 4 – 3 х 3 + 2 х 2 + 1, с = 3;
в) f (x) = х 4 – 2 х 3 – х 2 + х – 1, с = 1+ i.
1.5. Найдите кратность корня с многочлена f:
а) f (x) = 2 х 4 – 7 х 3 + 9 х 2 – 5 х + 1, с = 1;
б) f (x) = х 5 – 5 х 4 + 40 х 2 – 80 х + 48, с = 2.
1.6. Найдите значения а, при которых многочлен х 5 – ах 2 – ах + 1 имеет –1 корнем не ниже второй кратности.
Наибольший общий делитель
Наибольший общий делитель нескольких многочленов – это такой их общий делитель, который кратен любому их общему делителю. Если
d = НОД(f1, …, f n), то существуют такие многочлены u 1, …, un, что
d = u 1 f 1 +… + un fn.
Это выражение называется линейным представлением НОД.
Для нахождения НОД(f, g) и его линейного представления используется алгоритм Евклида. Он заключается в последовательном делении с остатком первого многочлена на второй, затем второго на остаток, и т.д. Последний ненулевой остаток есть НОД(f, g). С помощью получившейся цепочки делений находится линейное представление.
Пример 2.1. Найти НОД(f, g) и его линейное представление:
f = х 4 + 2 х 3 – х 2 + x + 1;
g = 2 х 3 – х – 1.
Решение. Выполняем цепочку делений с остатком:
Результаты делений записываем в следующем виде:
f = g × (1/2 x + 1) – ½ r 1, r 1 = x 2 – 5 x + 4;
g = r 1 × (2 x + 10) + 41 r 2, r 2 = x – 1; (*)
r 1= r 2 × (x – 4).
Последний ненулевой остаток r 2 = x – 1 и есть НОД(f, g). Его линейное представление находим с помощью формул (*):
r 1 = 2 f – 2 g × (1/2 x + 1) = 2 f – g × (x + 2);
41 r 2 = g – r 1 × (2 x + 10) = g – (2 f – g × (x + 2)) × (2 x + 10) =
= g – 2(2 x + 10) f + (x + 2)(2 x + 10) g = (4 x + 20) f + (2 x 2 + 14 x + 21) g;
НОД(f, g) = x – 1= r 2 = 
f + 
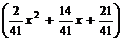g.
З а м е ч а н и е. Если не требуется находить линейное представление НОД, то при вычислениях числовые коэффициенты при получающихся остатках учитывать не требуется, и их можно отбрасывать. Чтобы в вычислениях избежать появления дробей, можно делимое перед выполнением деления умножить на подходящее целое число.
Упражнение 2.1. Найдите НОД(f, g) и его линейное представление:
а) f = х 6 – 4 х 5 + 11 х 4 – 27 х 3 + 37 х 2 – 35 x + 35;
g = х 5 – 3 х 4 + 7 х 3 – 20 х 2 + 10 x – 25.
б) f = 4 х 4 – 2 х 3 – 16 х 2 + 5 x + 9;
g = 2 х 3 – х 2 – 5 х + 4.
Кратные множители
Формальной производной многочлена f = a 0 + a 1 x + … + anxn над полем F называется многочлен f ¢ = a 1 + 2 a 2 x 2 + … + nanxn -1, где для k Î N, a Î F имеем 
.
Многочлены f и g называются ассоциированными, если они кратны друг другу. Многочлен f над кольцом К называется приводимым над К, если он ненулевой и его можно представить в виде произведения двух необратимых многочленов. Многочлен f называется неприводимым над К, если он необратим над К и любой его делитель ассоциирован с f или 1. Над полем неприводимы только многочлены положительной степени. Многочлен над полем разлагается в произведение неприводимых, и это разложение единственно с точностью до порядка и ассоциированности.
Многочлен f имеет неприводимый множитель p кратности k, если f M pk, f M pk +1. Множитель называется кратным, если его кратность больше 1.
Теорема 3.1. Если многочлен f над полем имеет неприводимый множитель p кратности k, то p – неприводимый множитель кратности k –1 для f ¢.
Эта теорема помогает решать задачу отделения кратных множителей многочлена f и разложения с помощью этого многочлена на множители. Для этого находим НОД(f, f ¢) = d. Многочлен d составлен из кратных множителей многочлена f, каждый из которых входит в d с кратностью на 1 меньшей, чем в f. Если удается разложить d на множители, то определяются все кратные множители многочлена f, и облегчается задача разложения его на множители. В противном случае можно рассмотреть многочлен 
. Он составлен из всех простых множителей многочлена f, взятых с кратностью 1. Если и этот многочлен не удается разложить, то можно, например, найти НОД(f 1, d), или применить описанный алгоритм к многочлену d.
Пример 3.1. Разложить на множители многочлен
f = x 5 – 15 x 3 – 10 x 2 + 60 x + 72.
Решение. Вычисляем f¢ = 5 x 4 – 45 x 2 – 20 x + 60 = 5(x 4 – 9 x 2 – 4 x + 12). Так как нам не требуется искать линейное представление НОД, то ненулевые числовые коэффициенты, которые выносятся из коэффициентов многочлена, можно отбрасывать. Поэтому вместо f¢ возьмем g = x 4 – 9 x 2 – 4 x + 12. Выполнив цепочку делений с остатком f на g согласно алгоритму Евклида, получаем
f = xg – 6 r 1, r 1 = x 3 + x 2 – 8 x – 12;
g = (x – 1) r 1.
Следовательно, d = НОД(f, f ¢) = r 1 = x 3 + x 2 – 8 x – 12. Так как степень НОД больше 2 и разложить его на множители достаточно затруднительно, то рассмотрим многочлен = x 2 – x – 6 = (x – 3)(x + 2). Так как f 1 имеет степень 2 и его удалось разложить на множители, то определены все неприводимые множители многочлена f, и осталось только определить их кратность. Сделаем это с помощью схемы Горнера.
| –15 | –10 | |||||
| –2 | –2 | –11 | ||||
| –2 | –4 | –3 | ||||
| –2 | –6 | |||||
| –2 | –8 | |||||
| –3 | ||||||
Ответ: f = (x + 2)3(x – 3)2.
Замечание. Так как в процессе решения мы полностью определили все простые множители многочлена f, то определять кратность множителя (x – 3) по схеме Горнера было не обязательно: так как степень многочлена равна 5 и кратность первого множителя первой степени равна 3, то кратность второго множителя должна быть равна 2.
Упражнения.
3.1. Разложите на множители многочлен:
а) f = x 6 – 6 x 4 – 4 x 3 + 9 x 2 + 12 x + 4;
б) f = x 5 – 6 x 4 + 16 x 3 – 24 x 2 + 20 x – 4.
3.2. Докажите, что многочлен x 2 n – nxn +1 + nxn –1 – 1 имеет число 1 тройным корнем.