Численное интегрирование
Пусть требуется вычислить определенный интеграл  .
.
Для решения поставленной задачи естественно воспользоваться формулой Ньютона–Лейбница. Однако даже для многих сравнительно простых элементарных функций  первообразная, хотя и существует, но не является элементарной, и ее нахождение может представлять собой более сложную задачу, чем исходная. Невозможно воспользоваться формулой Ньютона–Лейбница и тогда, когда функция
первообразная, хотя и существует, но не является элементарной, и ее нахождение может представлять собой более сложную задачу, чем исходная. Невозможно воспользоваться формулой Ньютона–Лейбница и тогда, когда функция  задана таблично.
задана таблично.
Формула прямоугольников
Основывается на определении определенного интеграла и его геометрического смысла.
Если заменить приближенно площадь элементарной криволинейной трапеции площадью прямоугольника с основанием  , и высотой равной значению функции в некоторой точке этого отрезка. При этом если использовать левый конец интервала получаем формулу левых прямоугольников:
, и высотой равной значению функции в некоторой точке этого отрезка. При этом если использовать левый конец интервала получаем формулу левых прямоугольников:
 , где
, где  ,
, 
Если использовать правый конец интервала получаем формулу правых прямоугольников:

Однако самый хороший результат дает использование значение функции в середине отрезка:
 .
.
Оценим погрешность.

Т.е. имеет второй порядок точности относительно  . При этом первые две формулы имеют лишь первый порядок точности.
. При этом первые две формулы имеют лишь первый порядок точности.
Численное интегрирование состоит в вычислении значения определенного интеграла на основании конечного числа значений подынтегральной функции.
Для приближенного нахождения определенного интеграла  подынтегральную функцию обычно заменяют некоторой более «простой» функцией
подынтегральную функцию обычно заменяют некоторой более «простой» функцией  . Вычислив затем интеграл
. Вычислив затем интеграл 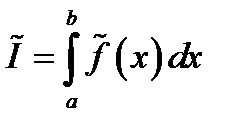 , приближенно полагают
, приближенно полагают  .
.
Часто в качестве заменяющей функции служит многочлен, причем обычно весь отрезок интегрирования разбивают на достаточное число меньших отрезков, и на каждом из них выполняют замену.
Формула трапеций
Заменяя на каждом из отрезков  функцию
функцию  многочленом первой степени (прямая), выполним интегрирование
многочленом первой степени (прямая), выполним интегрирование


 . Складывая эти равенства, придем к так называемой формуле трапеций.
. Складывая эти равенства, придем к так называемой формуле трапеций.
 .
.
Оценим погрешность.

Отсюда видно, что  , т.е., взяв
, т.е., взяв  достаточно большим, можно найти интеграл с любой заданной точностью. Действительно, пусть требуется вычислить интеграл с погрешностью не превосходящей
достаточно большим, можно найти интеграл с любой заданной точностью. Действительно, пусть требуется вычислить интеграл с погрешностью не превосходящей  , т.е.
, т.е.  . Это условие будет удовлетворено, если
. Это условие будет удовлетворено, если  , что равносильно
, что равносильно  .
.
Формула парабол
В этом случае отрезок интегрирования  разбивают на четное число
разбивают на четное число  отрезков. На каждом «сдвоенном отрезке»
отрезков. На каждом «сдвоенном отрезке»  заменяют функцию
заменяют функцию  многочленом второй степени (парабола).
многочленом второй степени (парабола).
Выполнив интегрирование


 и просуммировав результаты, получим так называемую формулу парабол (Симпсона):
и просуммировав результаты, получим так называемую формулу парабол (Симпсона):
 .
.
Погрешность метода можно оценить по формуле  . Это формула четвертого порядка точности относительно
. Это формула четвертого порядка точности относительно  . Здесь также можно утверждать, что
. Здесь также можно утверждать, что  , однако наличие в знаменателе
, однако наличие в знаменателе  вместо
вместо  приводит к тому, что, как правило, формула парабол обеспечивает большую точность при одинаковых значениях
приводит к тому, что, как правило, формула парабол обеспечивает большую точность при одинаковых значениях  , чем формула трапеций.
, чем формула трапеций.
Практическая оценка погрешности
Поскольку для определения числа разбиений 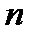 , обеспечивающих заданную точность
, обеспечивающих заданную точность  , необходимо вычислить значение максимума модуля второй или четвертой производных, что иногда оказывается затруднительным, на практике часто используют
, необходимо вычислить значение максимума модуля второй или четвертой производных, что иногда оказывается затруднительным, на практике часто используют
Правило Рунге: Пусть  значение интеграла, полученное при
значение интеграла, полученное при  разбиениях, а
разбиениях, а 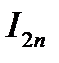 соответственно при
соответственно при  разбиениях, тогда если выполняется «с запасом»
разбиениях, тогда если выполняется «с запасом»  , то справедливо
, то справедливо  (
( для метода прямоугольников и трапеций,
для метода прямоугольников и трапеций,  для метода парабол).
для метода парабол).