Основы описания прямолинейных колебаний точки

Кафедра теоретической механики

КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

Методические указания и контрольные задания

для бакалавров всех специальностей

 

НОВОСИБИРСК 2017

 

 

Методические указания и контрольные задания разработали

В.Я. Рудяк, А.А. Белкин, С.Л. Краснолуцкий

 

 

Утверждены методической комиссией …

 

 

Рецензенты: П. В. Александров, канд. физ.-мат. наук,

доцент (НГАСУ (Сибстрин))

Е.В. Лежнев, канд. техн. наук,

доцент (НГТУ)

 

Новосибирский государственный

архитектурно-строительный

университет (Сибстрин), 2017

 

 

СОДЕРЖАНИЕ

 

 

Предисловие........................................................................................................ 4

1. Основы описания прямолинейных колебаний точки.......................... 5

1.1. Свободные незатухающие колебания (без учета сопротивления среды) 5

1.2. Свободные колебания при наличии постоянной силы................... 6

1.3. Свободные затухающие колебания (с учетом сопротивления среды). 7

1.4. Вынужденные колебания без учета сопротивления среды........... 7

1.5. Принципы решения задач на колебательное движение точки.... 8

2. Контрольное задание................................................................................... 9

3. Пример выполнения задания................................................................... 19

Список литературы......................................................................................... 24

 

 

Предисловие

 

Методические указания посвящены рассмотрению колебательного движения материальной точки. Данная тема является одной из наиболее важных в разделе «Динамика» курса теоретической механики.

При разработке указаний авторы опирались на новые образовательные стандарты для бакалавров, теоретический материал, изложенный в рекомендуемых студентам учебниках, собственный опыт чтения лекций и проведения практических занятий по теоретической механике, ряд методических указаний, использовавшихся ранее. В настоящей постановке включенные в контрольные задания задачи в большей степени соответствуют учебным программам бакалавров строительных специальностей.

Цель указаний – помочь студентам освоить теоретический материал и приобрести навыки применения теоретических положений к решению задач на колебательное движение материальной точки. Теоретический материал включает описание различных типов колебательного движения, контрольное задание содержит задачи на свободные незатухающие колебания точки. Задание позволяет для достаточно простых ситуаций научиться связывать удлинение пружины с координатой груза, формулировать начальные условия и использовать их в решении задачи, уяснить смысл статического удлинения. Для настоящих указаний были разработаны новые варианты контрольных задач.

Все принципиальные моменты выполнения индивидуального задания подробно изложены в приведенном примере. Прежде чем приступить к выполнению задания, студенту следует ознакомиться с соответствующим теоретическим материалом и разобрать пример решения задачи.

Основы описания прямолинейных колебаний точки

1.1. Свободные незатухающие колебания (без учета сопротивления среды). Рассмотрим колебания материальной точки (груза) на пружине (рис. 2.1), считая сначала, что сила тяжести не действует, и пренебрегая сопротивлением движению. Ось направим в сторону удлинения пружины, а начало координат возьмем в нижнем конце недеформированной пружины ( –длина недеформированной пружины). Тогда на груз действует единственная сила – сила упругости пружины , которая является восстанавливающей силой, поскольку она стремится вернуть груз в положение равновесия. Модуль силы упругости определяется законом Гука и при малых удлинениях пружины равен

, (1.1)

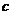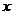где – коэффициент жесткости пружины (он показывает, какая сила необходима для растяжения пружины на один метр), а – ее удлинение. В выбранной нами системе координат удлинение равно координате груза , проектируя на ось второй закон Ньютона, получим дифференциальное уравнение (ДУ) свободных колебаний

или , (1.2)

где Его общее решение имеет вид

или . (1.3)

Такое движение материальной точки называется гармоническими колебаниями. Величина , равная максимальному отклонению точки от положения равновесия, называется амплитудой колебаний. Величина называется фазой, при этом 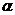– начальной фазой колебаний. Величину называют частотой. Промежуток времени , в течение которого совершается одно полное колебание, называется периодом.

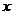Общее решение (1.3) зависит от двух произвольных постоянных, которые определяются из начальных данных: начального положения груза , и проекции на ось его начальной скорости . Легко убедиться, что

, . (1.4)

Из (1.3), (1.4) следуют два важных свойства свободных колебаний:

1. Амплитуда и начальная фаза колебаний зависят от начальных условий задачи.

2. Частота и период колебаний не зависят от начальных условий задачи и полностью определяются параметрами самой колебательной системы (в нашем примере системы из грузика и пружинки).

1.2. Свободные колебания при наличии постоянной силы. Рассмотрим, как влияет на свободные колебания постоянная сила. Пусть на груз, изображенный на рис. 1.1, действует сила тяжести 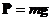(рис. 1.2). Заметим, что если бы груз находился в равновесии, то это означало бы, что сила тяжести уравновешивается силой упругости пружины, т.е. выполняется равенство , где 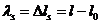– статическое удлинение пружины. Возьмем за начало отсчета оси 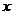точку , отстоящую от конца недеформированной пружины на расстоянии (см. рис. 1.2). Тогда удлинение пружины в этой системе координат равно . Составляя теперь уравнение Ньютона движения груза и проецируя его на ось 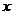, получим 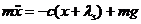, но поскольку , то в этой системе координат мы снова приходим к уравнению (1.2). Отсюда заключаем, что постоянная сила , не изменяя характера колебаний, смещает их центр в сторону ее действия на величину статического удлинения .

1.3. Свободные затухающие колебания (с учетом сопротивления среды). Пусть теперь на материальную точку действует еще сила сопротивления среды (воды, воздуха), пропорциональная скорости: . Записывая второй закон Ньютона и проектируя его на ось 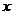с началом координат в положении статического равновесия пружины, приходим к уравнению

или

, (1.5)

где .

Здесь возможны три различных случая. В первом, когда сопротивление среды мало по сравнению с восстанавливающей силой, т.е. , общее решение уравнения (1.5) имеет вид

или . (1.6)

Постоянные интегрирования определятся из начальных условий и

, . (1.7)

Движение, таким образом, носит колебательный характер с частотой и периодом . Амплитуда колебаний убывает со временем по экспоненциальному закону.

В двух других случаях, когда или , решения можно записать соответственно так

и , (1.6а)

где . Следовательно, в этих двух случаях колебательное движение вообще не возникает, а движение материальной точки быстро затухает.

1.4. Вынужденные колебания без учета сопротивления среды. Пусть теперь наряду с восстанавливающей силой и силой тяжести на точку действует еще и сила 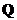, изменяющаяся по гармоническому закону: 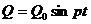, где 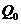– ее амплитуда, а – частота. Уравнение движения в системе координат с началом в положении статического равновесия тогда имеет вид

, (1.8)

где , 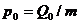. Это неоднородное дифференциальное уравнение, и его решение можно записать в форме , где – общее решение однородного уравнения (с нулевой правой частью), а – частное решение неоднородного уравнения (1.8). Но , частное же решение имеет вид . Поэтому движение точки описывается формулой

. (1.9)

Такое движение называют вынужденными колебаниями. Постоянные и a снова определяются из начальных условий задачи. Таким образом, движение точки слагается из собственных колебаний с амплитудой А (зависящей от начальных условий) и частотой k и вынужденных колебаний с амплитудой p ₀ / (k ² – p ²) (не зависящей от начальных условий) и частотой .

Решение (1.9) применимо лишь в случае, когда . Если собственная частота совпадает с частотой возмущающей силы p = k, решение можно представить в форме

. (1.10)

Амплитуда вынужденных колебаний, как мы видим, растет линейно со временем. Это явление называется резонансом.