На основе линейного уравнения множественной регрессии
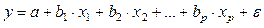
могут быть найдены частные уравнения регрессии:
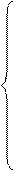
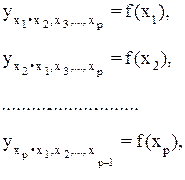
т.е. уравнения регрессии, которые связывают результативный признак с соответствующими факторами х при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения имеют следующий вид:
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем:
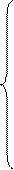
где 
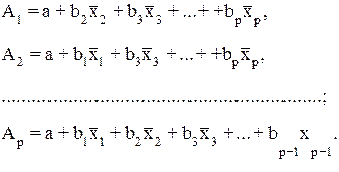
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии.
Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:
(3.4)
где bi – коэффициенты регрессии для фактора хi в уравнении множественной регрессии;
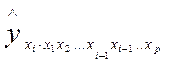– частное уравнение регрессии.
Частная корреляция
Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
Целесообразность внесения того или иного фактора в модель доказывается величиной показателя частной корреляции. Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влиянии других факторов, включённых в уравнение регрессии.
Если рассматривается регрессия с р факторами, то возможны частные коэффициенты корреляции первого, второго и так далее р - первого порядка:
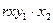- при постоянном действии фактора 
.
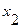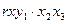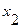- при постоянном действии факторов , 
.
- при постоянном действии факторов …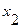 
.
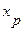Сопоставление коэффициентов частной корреляции разного порядка по мере увеличении числа внешних факторов показывает процесс “очищения” зависимости результатного признака с наследственным фактором. Хотя частная корреляция разных порядков удобна при анализе, в практических исследованиях предпочтение отдают показателям частной корреляции самого высоко порядка, так как эти порядки являются дополнительными к уравнению множественной регрессии.
Для линейной модели множественной регрессии 
коэффициент частной корреляции можно определить по формуле:
,
- множественный коэффициент детерминации всего комплекса p факторов с результатом.
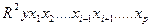- множественный коэффициент детерминации без введения в модель фактора 
.
Данный коэффициент частной корреляции позволяет измерить тесноту связи между y и xi при неизменном уравнении других факторов. Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается.
Коэффициенты парной корреляции называют коэффициентами нулевого порядка.
Коэффициенты частной корреляции более высоких порядков можно определить через коэффициент частной корреляции более низких порядков по рекуррентной формуле.
;
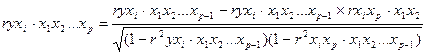Например, при двух факторах и i=1 данная формула имеет вид:
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициента корреляции первого порядка.
Подсчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1. А по формуле через множественные коэффициенты детерминации от 0 до 1.
В эконометрике частные коэффициенты корреляции не имеют самостоятельного значения. В основном их используют на стадии формирования модели в процедуре отсева факторов: строя многофакторную модель методом исключения переменных на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. Далее выбирается фактор с наименьшей несущественной по t - критерию величиной частного коэффициента корреляции.
Исключив данный фактор из модели, строится новое уравнение регрессии и процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля. Если исключён несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построение регрессионной модели почти не отличаются друг от друга, то есть 
, где р – число факторов.
Зная частные коэффициенты корреляции можно определить совокупный коэффициент корреляции по формуле: 
Отбор факторов
Спецификация модели. Отбор факторов при построении уравнения множественной регрессии
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой интеркорреляцией, может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором m факторов, то для нее рассчитывается показатель детерминации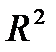 
, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии m факторов. Влияние других, не учтенных в модели факторов, оценивается как 1- 
с соответствующей остаточной дисперсией 
.
При дополнительном включении в регрессию m +1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:
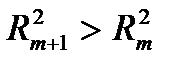и 
.
Если же этого не происходит и данные показатели практически не отличаются друг от друга, то включаемый в анализ фактор 
не улучшает модель и практически является лишним фактором.
Мультиколлинеарность
Мультиколлинеарность (multicollinearity) — в эконометрике (регрессионный анализ) — наличие линейной зависимости между объясняющими переменными (факторами) регрессионной модели. При этом различают полную коллинеарность, которая означает наличие функциональной (тождественной) линейной зависимости и частичную или просто мультиколлинеарность — наличие сильной корреляции между факторами.
Полная коллинеарность приводит к неопределенности параметров в линейной регрессиионной модели независимо от методов оценки. Рассмотрим это на примере следующей линейной модели
Пусть факторы этой модели тождественно связаны следующим образом: 
. Тогда рассмотрим исходную линейную модель, в которой к первому коэффициенту добавим произвольное число a, а из двух других коэффициентов это же число вычтем. Тогда имеем (без случайной ошибки):
Таким образом, несмотря на относительно произвольное изменение коэффициентов модели мы получили ту же модель. Такая модель принципиально неидентифицируема. Неопределенность существует уже в самой модели. Если рассмотреть 3-мерное пространство коэффициентов, то в этом пространстве вектор истинных коэффициентов в данном случае не единственный, а представляет собой целую прямую линию! Любая точка этой прямой — истинный вектор коэффициентов.В связи с этим проблема полной коллинеарности факторов решается уже на стадии отбора переменных при моделировании и поэтому к проблеме качества эконометрических оценок параметров отношения не имеет. На практике чаще возникает другая ситуация — сильная корреляция между факторами.
Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
1. Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл.
2. Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
28.Оценка параметров уравнения множественной регресии …..фото