Линейное пространство. Линейная зависимость и независимость векторов. Базис. Разложение вектора по базису.

.

Пусть дано непустое множество L элементов произвольной природы, которые будем обозначать ` а, ` b, ` c, ….

Определение 3.3.

Множество L называется линейным векторным пространством (или просто ЛП), если в L введены две операции «сложения» Å и «умножения на число» Ä такие, что для любых ` а,` b Î L и для любого числа a (действительного или комплексного) выполняются условия ` а Å` b Î L и aÄ Î L и эти операции удовлетворяют аксиомам:

1) ` а Å` b =` b Å` a

2) ` а Å` b

3) в L существует нулевой элемент`0 такой, что
" Î L Þ` а Å`0 =` a

4) " Î L существует противоположный элемент (– )Î L такой, что ` а Å(– ) =`0

5) 1Ä =

6) aÄ (bÄ ) = (ab)Ä

7) aÄ( Å` b) = (aÄ ) Å (aÄ )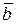

8) (a+b)Ä = aÄ Å bÄ .

Элементы линейного пространства называются векторами. ЛП называется действительным, если «умножение на число» определено для действительных чисел; если «умножение на число» определено для комплексных чисел, то ЛП называется комплексным ЛП.

Чтобы выяснить, является ли заданной множество ЛП, нужно:

1) задать операции Å и Ä (или проверить, что они заданы) так, чтобы результат этих операций был элементом данного множества.

2) проверить для этих операций выполнение всех восьми аксиом.

Докажите самостоятельно, что линейными пространствами (с естественным образом определенными на них операциями) являются:

- множество действительных чисел R;

- множество С_{[ a , b ]} непрерывных на [ a, b ] функций;

- множество Р _п [ x ] многочленов степени не выше п;

- множество матриц-строк длины п.

В дальнейшем для краткости операцию Å будем обозначать обычным знаком «+», а операцию Ä – также обычным символом умножения «.» или вообще опускать в записи, как это делается в алгебраических выражениях.

Рассмотрим совокупность (говорят: систему) векторов линейного пространства L: ₁, ₂, …, _k. Вектор ЛП L вида a_{1 1}+a_{2 2} + …+ a _{k k}. называется линейной комбинацией этих векторов, числа a _i – коэффициенты линейной комбинации.

Определение 3.4.

Система векторов { ₁, ₂, …, _k } ЛП L называется линейно зависимой, если существуют числа a₁, a₂, …, a _k, не все одновременно равные нулю, такие, что a_{1 1}+a_{2 2} + …+ a _{k k} =`0.

Если a_{1 1}+a_{2 2} + …+ a _{k k} =`0 тогда и только тогда, когда все коэффициенты этой линейной комбинации равны 0, то система векторов { ₁, ₂, …, _k } ЛП L называется линейно независимой.

Линейно независимая система { ₁, ₂, …, _k } называется максимально линейно независимой, если "` b Î L система { <sub>1</sub>, <sub>2</sub>, …, <sub>k</sub>,` b } – линейно зависима.

Если система { ₁, ₂, …, _k } максимально линейно независима, то равенство

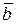a_{1 1}+ a_{2 2} + …+ a _{k k} + a _{k+ 1} =`0

выполняется, когда не все коэффициенты a _i = 0, причем обязательно a _{k+ 1}¹0. Тогда разделив обе части этого равенства на a _{k- 1}, можно записать его в форме

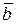= b_{1 1}+ b_{2 2} + …+ b _{k k},

т.е. представить вектор 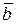в виде линейной комбинации векторов ₁, ₂, …, _k. При этом говорят, что вектор 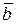разложен по векторам ₁, ₂, …, _k.

Можно доказать, что система векторов { ₁, ₂, …, _т } линейно зависима тогда и только тогда, когда хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов.

Определение 3.5.

Конечная упорядоченная максимально линейно независимая система векторов { ₁, ₂, …, _п } ЛП L называется базисом этого пространства.

Обозначают Б: { ₁, ₂, …, _п }. Если ЛП L имеет базис, то оно называется конечномерным, число векторов базиса называется размерностью ЛП L. Если хотят подчеркнуть, что ЛП L имеет размерность п (или, что то же самое, имеет базис, состоящий из п векторов), то пишут L_n.

Если система { ₁, ₂, …, _п } есть базис ЛП L, то "` b Î L существуют числа х ₁, х ₂, …, х_п такие, что

` b = х _{1 1}+ х _{2 2}+ …+ х_{п п}, (1)

Равенство (1) называется разложением вектора ` b по базису { <sub>1</sub>, <sub>2</sub>, …, <sub>п</sub> }. Числа х <sub>1</sub>, х <sub>2</sub>, …, х<sub>п</sub> (коэффициенты разложения) называют координатами вектора ` b в базисе { ₁, ₂, …, _п }. Тот факт, что числа х ₁, х ₂, …, х_п являются координатами вектора` b в базисе Б:{ ₁, ₂, …, _п } записывают так:

` b = (х ₁, х ₂, …, х_п)_Б.

Совокупность п чисел вида (х ₁, х ₂, …, х_п) называют числовой строкой длины п. По сути числовая строка длины п – это матрица-строка размерности п ´1. Поэтому над числовыми строками можно определить операции сложения и умножения на число так, как были определены эти операции для матриц. Множество всевозможных числовых строк длины п является линейным пространством размерности п и это пространство называется координатным пространством (или арифметическим пространством строк) и обозначается R ⁿ.

Множество свободных геометрических векторов образует линейное пространство. Пространство векторов плоскости обозначают V², множество векторов трехмерного пространства обозначают V³. Пространство векторов, расположенных на одной прямой (или параллельных одной прямой) обозначают V¹.

Справедлива теорема:

Теорема3.2.

Базис пространства V¹ образует любой ненулевой вектор.

Базис пространства V² образуют любые два ненулевых неколлинеарных вектора.

Базис пространства V³ составляют любые три ненулевых некомпланарных вектора.

Доказательство: Если совокупность ₁, ₂, …, _k. векторов линейного пространства является базисом, то равенство a_{1 1}+a_{2 2} + …+ a _{k k} =`0 выполняется тогда и только тогда, когда все коэффициенты a _i = 0 и " вектора 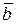выполняется равенство

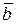= b_{1 1}+ b_{2 2} + …+ b _{k k},

где b _i – некоторые числа.

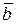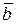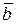1) Рассмотрим произвольный ненулевой вектор Î V¹. Равенство a =`0 выполняется только при a = 0. Так как все векторы V<sup>1</sup> лежат на одной прямой, то они коллинеарны, следовательно, для любого вектора ` а Î V¹ можно записать , значит, вектор образует базис в V¹.

2) Рассмотрим два произвольных ненулевых, неколлинеарных вектора ` а,` b Î V². Покажем, что равенство выполняется только при a = b = 0, и "` с Î V² $ х, у Î R², такие, что .

Предположим, что равенство верно при a ¹ 0, тогда получим

Þ , т.е. ,

значит, векторы ` а и ` b коллинеарны, что противоречит условию. Значит, a = b = 0.

Рассмотрим произвольный вектор ` с Î V<sup>2</sup>, пусть, например, (рис 5). Через точку С проведем прямую, параллельную вектору ` b, а через точку D – прямую, параллельную вектору` а. Тогда вектор параллелен вектору ` а и, значит, = х , а вектор параллелен вектору 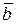и = у 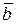. Следовательно, из треугольника, получаем

= ,

что и требовалось доказать.

Утверждение 3) доказать самостоятельно.

Равенство называется разложением вектора ` с по базису {` a,` b }, коэффициенты х и у этого разложения называются координатами вектора ` с в базисе {` a,` b }, запись ` с = (х, у) называется координатной формой вектора ` с.

Если ` a,` b, ` с – некомпланарные ненулевые векторы, то они образуют базис пространства V<sup>3</sup>, поэтому "` d Î V³ разложение по базису {` a,` b, ` с } имеет вид

,

а в координатной форме `d = (x, y, z).

Координатная форма вектора устанавливает соответствие между пространством геометрических векторов (V², V³) и пространством числовых строк (R² и R³ соответственно). Поэтому линейные операции над векторами в координатной форме выполняются по правилам действий над числовыми строками.

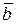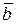Например,если два вектора и пространства V³ заданы своими координатами = (а_x, a_y, a_z) и = (b_x, b_y, b_z), то

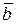= Û a_x = b_x, a_y = b_y, a_z = b_z;

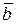± = (а_x ± b_x, a_y ± b_y, a_z ± b_z);

a = (a а_x, a a_y, a a_z).

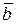Если векторы = (а_x, a_y, a_z) и = (b_x, b_y, b_z), коллинеарны, то выполняется равенство , откуда (а_x, a_y, a_z) = (l b_x, l b_y, l b_z), или

a_x = l b_x, a_y = l b_y, a_z = l b_z,

.

Значит, если векторы коллинеарны, то их координаты пропорциональны.

Наоборот, если координаты двух векторов пропорциональны, то имеем:

Þ (а_x, a_y, a_z) = (l b_x, l b_y, l b_z) Þ ,

а это значит, что векторы коллинеарны.

Таким образом, мы доказали: для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны.

Рассмотрим произвольную прямую l и на ней орт ` е. Этот орт порождает на прямой l семейство векторов, лежащих на этой прямой: . При l > 0 ` а 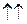` е, при l < 0 ` а 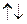` е, значит, орт` е определяет на прямой l два противоположных направления.

Прямая, на которой выбрано направление, называется осью, а орт, задающий это направление, называется ортом оси. Направление, сонаправленное с направлением орта, называется положительным, противоположное направление – отрицательным. Орт также определяет на оси масштаб и начало отсчета (точку его приложения). Проекция вектора на ость есть проекция вектора на орт оси:

Если в пространстве V³ выбрана точка О и произвольный базис { } с началом в точке О, то четверку {O, } называют репером. Говорят, что в V³ задана декартова система координат (афинная система координат), если в нем задан репер и с каждым вектором репера связана ось, называемая координатной осью. Первая из этих осей, соответствующая вектору ` е ₁, называется осью абсцисс, вторая – осью ординат, третья – осью аппликат. Обозначают систему координат обычно ОХУZ. Тогда каждой точке М трехмерного пространства ставится в соответствие тройка чисел М(х, у, z) – координат вектора (радиус-вектора этой точки) в базисе { }.

Аналогично вводится понятие системы координат на плоскости.

Обозначим ` i, ` j, ` k – взаимно перпендикулярные единичные векторы: , ` i ^` j ^` k. Очевидно, эти векторы образуют базис в V³. Базис называется о ртонормированным. Декартова система координат, порожденная репером {О,` i, ` j, ` k }, называется декартовой прямоугольной системой координат. Таким образом:

Декартовой прямоугольной системой координат в трехмерном пространстве называют совокупность

- некоторой точки О, называемой началом координат;

- ортонормированного базиса .

В дальнейшем мы будем рассматривать декартову прямоугольную систему координат (ДПСК).

В декартовой прямоугольной системе координат координаты вектора = (а_x, a_y, a_z) равны соответственно проекциям этого вектора на координатные оси: а_x = , a_y = , a_z = .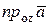

Базисные векторы ` i, ` j, ` k в ДПСК имеют координаты

` i = (1, 0, 0) ` j = (0, 1, 0) ` k = (0, 0, 1) в V³,

`i = (1, 0) ` j = (0, 1) в V².

Рассмотрим произвольный вектор Î V³, углы, которые этот вектор образует с осями координат (или с базисными ортами ` i, ` j, ` k) обозначим a = , b = , g = (рис.6). Косинусы этих углов cosa, cosb, cosg называются направляющими косинусами вектора . Направляющие косинусы заданного вектора обладают свойством

cos²a + cos²b + cos² g = 1.

Они характеризуют направление вектора относительно ДПСК.

Если известны координаты точек А(х _А, у _А, z _A) и B((х _B, у _B, z _B) – начала и конца вектора , то координаты этого вектора находят по правилу «от координат конца вектора отнять соответствующие координаты начала»:

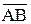= (х _B – х _А, у _В – у _А, z _B – z _A).