Раздел 2. Квадратичные формы и линейные операторы
Линейные операторы
Линейное (векторное) пространство
Пусть 
- множество элементов, для которых определены операции сложения и умножения на число, причём эти операции обладают следующими свойствами.
Для любых элементов 
, 
, 
из множества
1) 
(коммутативность сложения);
2) 
(ассоциативность сложения);
3) во множестве существует нулевой элемент 
такой, что для любого элемента 
, 
(существование нулевого элемента);
4) для любого элемента существует элемент 
, такой, что 
(существование противоположного элемента);
5) 
.
Для любых действительных чисел 
любых элементов , из множества ;
6) 
;
7) Распределительный закон 
;
8) 
.
Определение. Множество называется линейным (векторным) пространством, а его элементы называются векторами.
Примерами векторных пространств являются множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д.
Если операции сложения и умножения на число определены для действительных элементов, то линейное (векторное) пространство является вещественным пространством, если для комплексных элементов – комплексным пространством.
Свойства линейных пространств
1) В каждом линейном пространстве существует только один нулевой элемент .
2) Для каждого элемента существует только один ему противоположный элемент 
.
3) Для каждого элемента выполняется равенство ×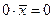 
;
4) Для каждого 
и 
выполняется равенство × 
;
5) Если 
, то 
или 
;
6) 
.
Линейные преобразования
Определение. Говорят, что в линейном пространстве задано некоторое линейное преобразование А, если любому элементу по некоторому правилу ставится в соответствие элемент 
.
Определение. Преобразование А называется линейным, если для любых векторов и 
и любого 
выполняются равенства
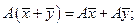
Определение. Линейное преобразование называется тождественным, если оно преобразует каждый элемент линейного пространства в себя.
.
Пример. Является ли А линейным преобразованием А = + 
; 
?
Запишем преобразование А для произвольного элемента : А = + . Проверим, выполняется ли правило операции сложения для этого преобразования: 
Очевидно, это равенство верно только при 
т.е. данное преобразование А нелинейное.
Определение. Если в пространстве существуют векторы линейного преобразования 
, то другой вектор 
является линейной комбинацией векторов 
.
Определение. Если 
выполняется только при 
, то векторы называются линейно независимыми.
Определение. Если в линейном пространстве есть n линейно независимых векторов, а любые 
векторов линейно зависимы, то пространство называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства .
Следствие. Любой вектор линейного пространства может быть представлен в виде линейной комбинации векторов базиса.
Матрицы линейных преобразований
Пусть в 
- мерном линейном пространстве с базисом 
, 
,…, 
задано линейное преобразование А. Тогда векторы 
, 
,…, 
- являются векторами этого пространства и их можно представить в виде линейной комбинации векторов базиса:
= 
+ 
+…+ 
,
= 
+ 
+…+ 
,
……………………………….
= + +…+ 
.
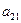
В этом случае матрица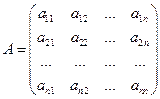 
называется матрицей линейного преобразованияА. Пусть = 
+ 
+…+ 
- произвольный вектор в пространстве . Тогда
; 
,
где
,
,
……………………………..
.
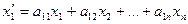Эти равенства называются линейным преобразованием в базисе , ,…, .
В матричном виде
; 
; 
.
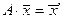Пример. Найти матрицу линейного преобразования, заданного в виде
;
;
.
На практике действия над линейными преобразованиями сводятся к действиям над их матрицами.
Определение. Если вектор переводится в вектор линейным преобразованием с матрицей А, а вектор в вектор 
линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор в вектор (оно называется произведением составляющих преобразований).
.
Пример. Задано линейное преобразование А, переводящее вектор в вектор и линейное преобразование В, переводящее вектор в вектор . Найти матрицу линейного преобразования, переводящего вектор в вектор .
т.е. 
Замечание. Если 
то преобразование является вырожденным.