Локальные свойства непрерывной функции.

Лекция №4.

1.Понятие непрерывности функции в точке.

2.Локальные свойства непрерывной функции.

3.Использование непрерывности при вычислении пределов.

Виды неопределенных выражений.

Понятие непрерывности функции в точке.

Когда мы вводили определения предела функции, мы не требовали, чтобы функция в точке x₀ была определена.

Большой интерес представляет случай если функция в точке x₀ определена и значения f (x₀) совпадает со значением предела.

Опр. 1. Пусть функция f (x) определена в точке x₀ и в некоторой окрестности точки x₀. Функция f (x) называется непрерывной в точки x₀ , если

Дадим это определение на языке «ε-δ».

Опр.2.

 

 

Введем обозначения: x -x₀= ∆ x – приращение аргумента;

f (x)- f (x₀)= ∆y – приращение функции.

или

 

Опр.3. Функция f(x) называется непрерывной в точке x₀, если она определена в самой точке x₀ и в некоторой ее окрестности О(x₀) и при этомб.м. приращению аргумента соответствует б.м. приращение функции, т.е. .

Пример. Исходя из определения, убедится, что непрерывна при любом х.

Решение: Используем определение на «языке приращений».

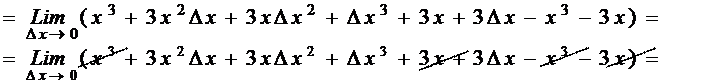
Локальные свойства непрерывной функции.

Рассмотрим несколько основных теорем о непрерывных функциях.

Теорема1. Если функция y=f(x) непрерывная в точке x₀, то она является ограниченной в некоторой окрестности О(x₀).

Доказательство: Воспользуемся определением.

 

 

Мы должны показать, что

Запишем равносильные неравенства.

;

ограничена в

Теорема 2. Если функции f(x) и g(x) непрерывны в точке x₀, тогда их сумма, произведение и частное тоже будут непрерывны в точке x₀, причем непрерывна при g(x) ≠ 0.

Доказательство: Т.к. f(x) и g(x) непрерывны в точке x₀, то ,

Согласно определению 1, это означает непрерывность суммы. Непрерывность частного и произведения доказывается аналогично (самостоятельно).

Теорема 3. (о непрерывности сложной функции).

Пусть функции y=f(u) и u=g(x) определяют сложную функцию y=f(g(x)) на X. Если u=g(x) непрерывна в точке x₀, а y=f(u)- непрерывна в точке u₀, причем u₀=g(x₀), тогда сложная функция y=f(g(x)) непрерывна в точке x₀.

Доказательство:

Дадим аргументу x₀ приращение ∆x, такое чтобы . Тогда функция u=g(x) получит приращение ∆u, функция y=f(u) - получит приращение ∆y. Т.к. u=g(x) непрерывна в точке x₀, тогда , а y=f(u) непрерывна в точке u₀, . Отсюда следует, что , а это означает, что y=f(g(x)) непрерывна в точке x₀.

Теорема 4. Каждая из простейших элементарных функций непрерывна в своей области определения.

Непрерывность каждой функции доказывается отдельно.

Например, докажем, что y=sin x непрерывна в точке x₀.

∆y=sin(x₀+∆x)-sin x₀= ;

=

 

y=sin x непрерывная в точке x_0.

Следствие. Любая функция, полученная путем суперпозиции простейших элементарных функций, будет непрерывной.

Определение. Функция, непрерывная в каждой точке множества Х называется непрерывной на множестве Х.

Например, y=sin x непрерывна на х (-∞;+ ∞), y=ln x, на x (0;+∞).

Если функция определена на замкнутом промежутке, то для нее используется понятие односторонней непрерывности в точках x=a и x=b.

Опр. 4. Функция y=f(x) называется непрерывной слева в точке x₀, если и справа если .

Очевидно, что непрерывная в точке x₀ функция будет в этой точке непрерывной слева и справа.

3.Ипользование непрерывности при вычислении пределов. Виды неопределенных выражений.

Пусть требуется найти . Если f(x) непрерывна в точке х₀, тогда , а это означает, что при нахождении предела в f(x) достаточно вместо х поставить х₀.

Например: показать,что функция f(x)=ln(sinx)+cos²2x непрерывна в точке х₀=π/2;

Решение:

при решении такого сорта задач можно использовать теоремы о пределах, а также свойства б.м. и б.б. величин.

Исключение составляют неопределенные выражения. Пусть:

, , , ,

Тогда неопределенным при x→ x₀ будут выражения:

, , ,

 

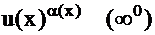
Для раскрытия неопределенных выражений каждого типа существует свои приемы.

Пример.1

Пример2.

 

Пример3. Найти: