Пусть, изучая неизвестную функциональную зависимость между y и x, в результате серии экспериментов произвели ряд измерений этих величин и получили таблицу значений
| x0 | x1 | x2 | … | xn |
| y0 | y1 | y2 | … | yn |
Задача состоит в том, чтобы найти приближенную зависимость
 (8)
(8)
значения которой при 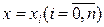 мало отличаются от опытных данных
мало отличаются от опытных данных  . Приближенная функциональная зависимость (8), полученная на основании экспериментальных данных, называется эмпирической формулой.
. Приближенная функциональная зависимость (8), полученная на основании экспериментальных данных, называется эмпирической формулой.
Задача построения эмпирической формулы отличается от задачи интерполирования. График эмпирической зависимости, вообще говоря, не проходит через заданные точки  , как в случае интерполяции. Это приводит к тому, что экспериментальные данные в некоторой степени сглаживаются, а интерполяционная формула повторила бы все ошибки, имеющиеся в экспериментальных данных.
, как в случае интерполяции. Это приводит к тому, что экспериментальные данные в некоторой степени сглаживаются, а интерполяционная формула повторила бы все ошибки, имеющиеся в экспериментальных данных.
Построение эмпирической формулы состоит из двух этапов: подбор общего вида этой формулы и определения наилучших значений содержащихся в ней параметров.
В методе наименьших квадратов в качестве эмпирической функции выбран многочлен. Согласно этому методу за меру отклонения многочлена
 (9)
(9)
от данной функции  на множестве точек
на множестве точек  ,
,  , …,
, …,  принимают величину
принимают величину
 , (10)
, (10)
равную сумме квадратов отклонений многочлена  от функции
от функции  на заданной системе точек.
на заданной системе точек.
Очевидно, что  есть функция коэффициентов
есть функция коэффициентов  ,
,  , …,
, …,  . Эти коэффициенты надо подобрать так, чтобы величина
. Эти коэффициенты надо подобрать так, чтобы величина  была наименьшей. Полученный многочлен называется аппроксимирующим для данной функции, а процесс построения этого многочлена – точечной квадратичной аппроксимацией или точечным квадратичным аппроксимированием функции.
была наименьшей. Полученный многочлен называется аппроксимирующим для данной функции, а процесс построения этого многочлена – точечной квадратичной аппроксимацией или точечным квадратичным аппроксимированием функции.
Для решения задачи точечного квадратичного аппроксимирования воспользуемся общим приемом дифференциального исчисления. Найдем частные производные от величины
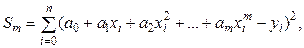
где  по всем переменным
по всем переменным 
 , …,
, …,  . Приравнивая эти частные производные к нулю, получим для определения неизвестных
. Приравнивая эти частные производные к нулю, получим для определения неизвестных 
 , …,
, …, 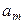 систему m+ 1 уравнений с m+ 1 неизвестными:
систему m+ 1 уравнений с m+ 1 неизвестными:
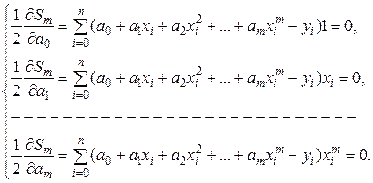 (11)
(11)
Введем обозначения:
 ,
, 
 ,
, 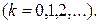
Преобразуя систему (11) и используя введенные обозначения, будем иметь:
 (12)
(12)
где  .
.
Можно доказать, что если среди точек  ,
,  , …,
, …,  нет совпадающих и
нет совпадающих и  , то определитель системы (12) отличен от нуля и, следовательно, эта система имеет единственное решение
, то определитель системы (12) отличен от нуля и, следовательно, эта система имеет единственное решение  ,
,  , …,
, …,  . Многочлен (9) с такими коэффициентами будет обладать минимальным квадратичным отклонением
. Многочлен (9) с такими коэффициентами будет обладать минимальным квадратичным отклонением  .
.
Таким образом, аппроксимирование функций представляет собой более общий процесс, чем интерполирование.
Для составления системы (11) рекомендуется схема способа наименьших квадратов, приведенная в таблице 1, где принято m= 2.
Таблица 1

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
|  
|  
| |

| 
| 
| 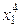
| 
|  
|  
| |

| 
| 
| 
| 
|  
|  
| |

| 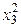
| 
| 
| 
|  
| 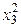 
| |

| 
| 
| 
| 
|  
|  
| |

| 
| 
| 
| 
| 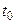
| 
| 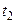
|
Пример. Подобрать аппроксимирующий многочлен второй степени  для данных
для данных

| 0.78 | 1.50 | 2.34 | 3.12 | 3.81 |

| 2.50 | 1.20 | 1.12 | 2.25 | 4.28 |
Решение. Вычисления, которые нам нужно произвести, расположим по схеме (для m =2, n =4), приведенной в таблице 1.
Для данного примера получаем таблицу 2 (вычисления проводятся с тремя десятичными знаками).
Таблица 2

| 
| 
| 
| 
| 
| 
| 
|
| 0.78 | 0.608 | 0.475 | 0.370 | 2.50 | 1.950 | 1.520 | |
| 1.56 | 2.434 | 3.796 | 5.922 | 1.20 | 1.872 | 2.921 | |
| 2.34 | 5.476 | 12.813 | 29.982 | 1.12 | 2.621 | 6.133 | |
| 3.12 | 9.734 | 30.371 | 94.759 | 2.25 | 7.020 | 21.902 | |
| 3.81 | 14.516 | 55.306 | 210.717 | 4.28 | 16.307 | 62.128 | |
| 11.61 | 32.768 | 102.761 | 341.750 | 11.35 | 29.770 | 94.604 |
Отсюда система для определения коэффициентов  ,
,  ,
,  :
:
 (13)
(13)
Решив систему (13), получим  ,
,  ,
,  . Следовательно, искомый многочлен есть
. Следовательно, искомый многочлен есть
 (14)
(14)
Сравним исходные значения для  с соответствующими значениями
с соответствующими значениями  , полученными из приближенной формулы (14). Соответствующие результаты приведены в таблице 3.
, полученными из приближенной формулы (14). Соответствующие результаты приведены в таблице 3.
Таблица 3

| 
| 
| 
|
| 0.78 | 2.50 | 2.505 | 0.005 |
| 1.56 | 1.20 | 1.194 | 0.006 |
| 2.34 | 1.12 | 1,110 | 0.010 |
| 3.12 | 2.25 | 2.252 | 0.002 |
| 3.81 | 4.28 | 4.288 | 0.008 |
Задание 3
Подобрать аппроксимирующий многочлен второй степени  для функции из задания 2.
для функции из задания 2.
4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Постановка задачи. Вычисление корней уравнения - одна из важнейших математических задач. Сравнительно редко удаётся найти точные значения корней. Поэтому важное значение приобретают способы приближённого нахождения корней уравнения и оценка степени их точности.
Пусть дано уравнение с одним неизвестным вида
 , (15)
, (15)
где  - непрерывная функция переменной x. Требуется найти корень этого уравнения. Представить решение этого уравнения в виде конечной формулы оказывается невозможным, поэтому мы откажемся от поиска точного значения корней и займёмся их приближённым вычислением с заданной точностью.
- непрерывная функция переменной x. Требуется найти корень этого уравнения. Представить решение этого уравнения в виде конечной формулы оказывается невозможным, поэтому мы откажемся от поиска точного значения корней и займёмся их приближённым вычислением с заданной точностью.
Основные этапы решения. Решение задачи отыскания корней осуществляется в два этапа. Первый этап называется этапом отделения (локализации) корней, второй - итерационного уточнения корней.
Известно, что если функция f(x) непрерывна и принимает на концах отрезка [ a,b ] значения разных знаков, т.е. f(a)f(b)<0, то внутри этого промежутка имеется хотя бы один корень уравнения.
Геометрически это означает, что график непрерывной функции, расположенной по разные стороны оси OX, пересекает эту ось, по меньшей мере, в одной точке.
Отрезок [ a,b ], содержащий только один корень уравнения f(x), называется отрезком локализации корня. Цель этапа локализации считается достигнутой, если для каждых подлежащих определению корней удалось указать отрезок локализации.
К сожалению, универсальный метод локализации не представляется возможным. В простых ситуациях хороший результат может давать графический метод. Часто применяется построение таблиц значений функций вида yi = f(xi), i= 1,2,… и при этом о наличии корня на отрезке [ xi, xi+1 ], судят по перемене знака функции на концах отрезка.
Пример 1. Локализуем корни уравнения
4-2 x 2 -ex= 0.
Для этого преобразуем уравнение к виду 4-2 x2= ex и построим графики функций y= 4-2 x 2и y=ex. Абсциссы точек пересечения этих графиков являются корнями данного уравнения. Из графика, изображенного на рис. 1, видно, что уравнение имеет два коня, расположенные на отрезках [-2,-1] и [0,1].

Рис. 1
Пример 2. Локализуем корни уравнения
x 3 - 1.1 x 2 - 2.2 x +1.8=0.
Для этого составим таблицу значений функции F(x)= x 3 - 1.1 x 2 - 2.2 x +1.8 на отрезке [-2,2] с шагом 0.4.

| -2 | -1.6 | -1.2 | -0.8 | -0.4 | |

| -6.2 | -1.592 | 1.128 | 2.344 | 2.44 | 1.8 |

| 0.4 | 0.8 | 1.2 | 1.6 | 2.0 |

| 0.808 | -0.152 | -0.696 | -0.44 |
Из таблицы видно, что функция f меняет знак на концах отрезков [-1.6, -1.2], [0.4, 0.8], [1.6, 2.0]. Поэтому каждый из этих отрезков содержит, по крайней мере, один корень. Учитывая, что f(x) - многочлен третьей степени, который не может иметь более трех корней, то задача локализации решена.
После локализации корней производится итерационное уточнение каждого корня одним из методов. Рассмотрим метод половинного деления.
Метод половинного деления. Пусть дано уравнение (15), причем функция f(x) непрерывна на [ a,b ] и f(a)f(b)<0. Для вычисления корня уравнения (15), принадлежащего отрезку [ a,b ], найдем середину этого отрезка  . Если
. Если  , то для продолжения вычислений выберем ту из частей данного отрезка [ a, x0 ] или [ x0, b ], на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначим через a1 и b1.
, то для продолжения вычислений выберем ту из частей данного отрезка [ a, x0 ] или [ x0, b ], на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначим через a1 и b1.
Новый отрезок [ a1, b1 ] снова делим пополам и проводим те же рассуждения и т. д. В результате получаем на каком-то этапе или точный корень уравнения (15), или же бесконечную последовательность вложенных отрезков [ a, b ], [ a1, b1 ],…, [ an, bn ], таких что
f(an)f(bn)>0 (n =1,2,…), (16)
 (17)
(17)
Число  - общий предел последовательностей { an } и { bn } - является корнем уравнения f(x)=0.
- общий предел последовательностей { an } и { bn } - является корнем уравнения f(x)=0.
Оценку погрешности на n -ом шаге вычислений можно получить из соотношения (17) в виде
 . (18)
. (18)
Здесь  с точностью
с точностью  , не превышающей
, не превышающей  .
.
Если требуется найти корень уравнения с точностью  , то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 2
, то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 2  . Тогда координата середины отрезка и есть значение корня с требуемой точностью.
. Тогда координата середины отрезка и есть значение корня с требуемой точностью.
Метод деления пополам сходится для любых непрерывных функций, устойчив к ошибкам округления и легко реализуется на ЭВМ.
Задание 4
Отделить корни уравнения и найти их с точностью  =0,01 методом деления пополам. Сделать чертеж.
=0,01 методом деления пополам. Сделать чертеж.
0.  1.
1.  2.
2. 
3.  4.
4. 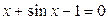 5.
5. 
6.  7.
7.  8.
8. 
9. 