Полигоны, или многоугольники, состоят из граней (faces). Одна грань представляет собой плоскую поверхность, полученную соединением трех точек, называемых вершинами (vertex). Положение вершин определяет форму и размер грани. Линии, соединяющие вершины друг с другом, называются ребрами (edges). Как правило, полигональные грани имеют три вершины, но могут иметь и четыре вершины и, соответственно, как треугольную, так и четырехугольную форму.
Грани соединяются друг с другом вдоль ребер, формируя более сложную поверхность (рис. 4.2).
Рис. 4.2. Полигональная сфера и составляющие ее подобъекты
Полигональные модели проще всего визуализируются, и именно по этой причине они обычно используются в игровых приложениях, где визуализация должна происходить прямо по ходу игры. Для игр также предпочтительно создавать объекты, состоящие из небольшого числа полигонов, чтобы максимально ускорить
процесс визуализации. Модели с плотной сеткой обычно используются в кино 11 на телевидении. Благодаря возможности создания моделей из одного куска данный формат применяется для получения персонажей. Персонажи в процессе анимации деформируются различными способами, поэтому крайне выгодно иметь модель, которая не будет разламываться в области швов.
5. Воксельные модели имеют определенное разрешение. Каждый воксел имеет определенное значение, например, цвет.
Для хранения воксельной модели применяют массив размерами X×Y×Z. Несжатые воксельные модели (по сравнению с векторными) потребляют гораздо больше места в памяти для обработки. К примеру, одна несжатая модель размером 256×256×256 вокселей будет занимать память объёмом от 32 Мб (256*256*256=16777216 вокселей и как минимум 2 байта на воксель даже в 256-ти градациях серого, так как к ним надо добавить 256 градаций прозрачности, итого 16777216*2=33554432 байт=33554432/1024=32768 Кб = 32768/1024=32 Мб), в то время как векторной модели может потребоваться в десятки или даже сотни раз меньше.
Понятие растра
Идеи разработки воспроизведения полутоновых изображений возникли в полиграфии очень давно. Однако только в 1881 году георг Майзенбах заложил основы растрирования. Майзенбах получил воспроизводимую растровую структуру с помощью периодической решетки и, таким образом, осуществил передачу полутонов.
Понятие растра является одним из основополагающих в полиграфии. Растр является оптическим инструментом, необходимым для преобразования непрерывного полутонового изображения в точечное. Без процесса растрирования было невозможно воспроизводить полутона способами офсетной и высокой печати. Растром называют и точечную структуру полученного изображения, состоящего из различных по размеру растровых точек (растровых величин), т.е. печатных элементов. Точки обладают разным диаметром, однако расстояния между центрами точек равны. В местах, где рисунок имеет абсолютно черный цвет (при черно-белой печати), точки столь велики по размеру, что перекрывают друг друга, не оставляя светлого места. В абсолютно белых местах, напротив, диаметр точки равен нулю, поэтому краска там отсутствует, и получается белый цвет. Растровые точки иногда можно разглядеть невооруженным глазом - к примеру, в иллюстрациях низкого качества в газетах.
Качество печати определяется линеатурой растра. Линеатура растра - это количество линий, на пересечении которых размещены растровые точки, в единице длины изображения. Чем больше растровых точек на единицу площади, тем качественнее и естественнее выглядит изображение. Линеатура растра - близость растровых точек друг к другу,и чем она выше (больше точек на единицу площади), тем легче различить мелкие детали изображения.
Линиатура растра измеряется в л/д (линии на дюйм) или л/см (линии на сантиметр). В рекламной печати высокого качества стараются применять высоколиниатурные растры (150 л/д). Однако никогда не следует забывать, что полиграфия - сложный процесс, и результат сложной полиграфической цепочки зависит от множества факторов. Желательно эти факторы учитывать, так как если печатное оборудование типографии низкого класса, делать фотоформу с высокой линиатурой нет смысла. Также не нужны слишком высокие линиатуры при печати больших плакатов, постеров, афиш, ведь при рассматривании этих изделий полиграфии с большого расстояния даже крупные растровые точки сольются, и изображение мы будем воспринимать качественным.
7. Интерполирование сплайнами
Интерполяционные формулы Лагранжа, Ньютона и Стирлинга и др. при использовании большого числа узлов интерполяции на всем отрезке [ a, b ] часто приводят к плохому приближению из-за накопления погрешностей в процессе вычислений [2]. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязательно приводит к повышению точности. Для снижения погрешностей весь отрезок [ a, b ] разбивается на частичные отрезки и на каждом из них функцию 
заменяют приближенно полиномом невысокой степени. Это называется кусочно-полиномиальной интерполяцией.
Один из способов интерполирования на всем отрезке [ a, b ] является интерполирование сплайнами.
Сплайном называется кусочно-полиномиальная функция, определенная наотрезке [ a, b ] и имеющая на этом отрезке некоторое количество непрерывных производных. Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – в сходимости и устойчивости вычислительного процесса.
Рассмотрим один из наиболее распространенных в практике случаев – интерполирование функции кубическим сплайном.
Пусть на отрезке [ a, b ] задана непрерывная функция . Введем разбиение отрезка:
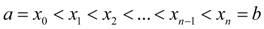(6)
и обозначим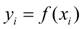 
, 
.
Сплайном, соответствующим данной функции и узлам интерполяции (6) называется функция 
, удовлетворяющая следующим условиям:
1) на каждом отрезке 
, 
функция является кубическим многочленом;
2) функция , а также ее первая и вторая производные непрерывны на отрезке [ a, b ];
3) 
Третье условие называется условием интерполирования. Сплайн, определяемый условиями 1) – 3), называется интерполяционным кубическим сплайном.
Рассмотрим способ построения кубического сплайна [2].
На каждом из отрезков , будем искать сплайн-функцию 
в виде полинома третьей степени:
(7)
где 
искомые коэффициенты.
Продифференцируем (7) трижды по х:
откуда следует
Из условия интерполирования 3) получаем:
. (8)
Кроме того, будем считать 
.
Из условий непрерывности функции вытекает:
Отсюда с учетом (7) получим:
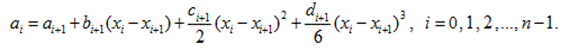
Обозначив 
и опуская промежуточные выкладки [2], окончательно получим систему уравнений для определения коэффициентов 
:
(9)
В силу трехдиагональности матрицы коэффициентов система (9) имеет единственное решение [2]. Найдя коэффициенты , остальные коэффициенты определим по явным формулам:
(10)
Таким образом, существует и найден единственный кубический сплайн, удовлетворяющий условиям 1) – 3).
Сплайн-интерполяция.
Определение 3.2 Сплайн (англ. spline - рейка, линейка) - это определенная в некоторой области G ∈ Rn кусочно-полиномиальная функция из класса Cr(G).
Таким образом в соответствии с определением существует разбиение области G на подобласти такое, что внутри каждой подобласти сплайн представляет собой полином некоторой степени М.
Определение 3.3 Интерполяция при помощи сплайнов называется сплайн-интерполяцией.
Рассмотрим одномерный случай (n=1) и наиболее употребительную кубическую сплайн-интерполяцию (M=3) из класса C2 (r=2).
Математическая постановка.
Пусть известные значения некоторой функции f(x) образуют таблицу 3.2 на отрезке [ a,b ], где a ≡ x0 < x1 <... < xN ≡ b
| x | x0 | x1 | ... | xN |
| f | f0 | f1 | ... | fN |
Таблица 3.2: Табличная функция.
Требуется построить по данной таблице интерполяционный кубический сплайн из класса C2, то есть функцию g(x) со следующими свойствами:
1) g(x) 
C2 [ a,b ]
2) на любом отрезке [ xi-1, xi ], i = 1,..., N функция g(x) является полиномом третьей степени,
3) g(xi) = fi, i = 0,..., N.
Для однозначного решения этой задачи добавим следующее часто используемое условие:
4) g''(a)=g''(b)=0
ТЕОРЕМА 3.3 Функция, удовлетворяющая свойствам 1)-4), существует и единственна.
ДОКАЗАТЕЛЬСТВО Так как по свойству 1) функция g''(x) непрерывна на [ a,b ] и по свойству 2) линейна на каждом отрезке [ xi-1 - x ], i= 1,...,N то можно записать 
x [ xi-1,xi ] следующее представление:
| g''(x) = mi-1(xi - x)/hi + mi(x - xi-1)/hi | (3.7) |
где hi=xi-xi-1, mi=g''(xi). Проинтегрируем равенство (3.7) дважды. Получим:
| g(x) = mi-1(xi - x)3/6hi + mi(x - xi-1)3/6hi + Ai(xi - x)/hi + Bi(x - xi-1)/hi | (3.8) |
где Ai, Bi - некоторые константы интегрирования. Найдем Ai и Bi, подставляя значения xi и xi-1 в (3.8):
fi = g(xi) = mi hi2/6 + Bi, следовательно, Bi = fi - mi hi2/6
fi-1 = g(xi-1) = mi-1 hi2/6 + Ai, следовательно Ai = fi-1 - mi-1 hi2/6
Подставляя Ai и Bi в (3.8) получим равенство:
| g(x) = mi-1(xi - x)3/6hi + mi(x - xi-1)3/6hi + (fi-1 - mi-1 hi2/6)(xi - x)/hi + (fi - mi hi2/6)(x - xi-1)/hi | (3.9) |
Тогда производная функции g(x) на [ xi-1,xi ] имеет вид:
| g'(x) = -mi-1(xi - x)2/2hi + mi(x - xi-1)2/2hi + mi-1 hi/6 - mi hi/6 + (fi - fi-1)/hi | (3.10) |
Пользуясь формулой (3.10) найдем односторонние (слева и справа) пределы функции g'(x) в точках xi, i = 1,..., N:
g'(xi - 0) = mi-1 hi /6 + mi hi /3 + (fi - fi-1)/hi;
g'(xi + 0) = -mi hi+1 /3 - mi+1 hi+1 /6 + (fi+1 - fi)/hi+1
(последнее равенство получено из (3.10) заменой индекса i на i+1, то есть переходом на отрезок [ xi,xi+1 ]). Так как по свойству 1) функция g'(x) непрерывна на отрезке [ a,b ], то приравнивая g'(xi+0) и g'(xi-0), i = 1,..., N-1 получаем N-1 уравнение:
| mi-1 hi /6 + mi (hi + hi+1)/3 + mi+1 hi+1 /6 = (fi+1 - fi)/hi+1 - (fi - fi-1)/hi, i = 1,..., N-1 | (3.11) |
Учитывая, что по свойству 4) имеют место равенства
| g''(x0) ≡ m0=0, g''(xN) ≡ mN=0 | (3.12) |
получаем линейную алгебраическую систему для нахождения неизвестных m1,..., mN-1:
| (3.13) |
где
Очевидно, что матрица A имеет строгое диагональное преобладание. Но из курса алгебры известно, что такие матрицы невырождены.
Следовательно, система 
однозначно разрешима относительно вектора 
, а тем самым функция со свойствами 1)-4) существует, единственна и представляется формулой (3.9).
ЗАМЕЧАНИЕ 3.7 На практике сплайн вычисляется на каждом отрезке [ xi-1, xi ], i = 1,..., N по формуле (3.9), с использованием табличной функции 3.2, равенств (3.12) и вектора 
, являющегося решением системы (3.13).
Оценку погрешности при сплайн-интерполяции дает следующее
УТВЕРЖДЕНИЕ 3.3 [3, стр.148] Если интерполируемая функция f(x) C 4 [ a,b ], то для функции погрешности R(x)=f(x)-g(x) справедливо неравенство:
| (3.14) |
где 
Меньше ограничений на функцию f(x) накладывает
УТВЕРЖДЕНИЕ 3.4 [11, стр.98] Если интерполируемая функция f(x) C 3 [ a,b ] и разбиение отрезка [ a,b ] узлами интерполяции является равномерным (h=hi=const), то для функции погрешности R(x)=f(x)-g(x) справедливо неравенство:
| (3.15) |
где 
Определение
Кривая Безье — параметрическая кривая, задаваемая выражением
где 
— функция компонент векторов опорных вершин, а 
— базисные функции кривой Безье, называемые также полиномами Бернштейна.
,
где 
— число сочетаний из 
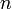по 
, где 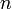— степень полинома, — порядковый номер опорной вершины.
[править]Виды кривых Безье
[править]Линейные кривые
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P 0 и P 1 определяют его начало и конец. Кривая задаётся уравнением:
.
[править]Квадратичные кривые
Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P 0, P 1 и P 2.
.
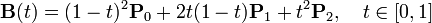Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах.
[править]Кубические кривые
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
.
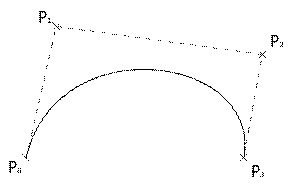
Кубическая кривая Безье
Четыре опорные точки P 0, P 1, P 2 и P 3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.
Линия берёт начало из точки P 0 направляясь к P 1 и заканчивается в точке P 3 подходя к ней со стороны P 2. То есть кривая не проходит через точки P 1 и P 2, они используются для указания её направления. Длина отрезка между P 0 и P 1 определяет, как скоро кривая повернёт к P 3.
В матричной форме кубическая кривая Безье записывается следующим образом:
,
где 
называется базисной матрицей Безье:
В современных графических системах и форматах, таких как PostScript (а также основанные на нём форматы Adobe Illustrator и Portable Document Format (PDF)), Scalable Vector Graphics (SVG), Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых. SVG также позволяет работать со сплайнами Безье 4-й степени[1].
Построение кривых Безье
[править]Линейные кривые
Параметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P 0 до P 1 находится B (t). Например, при t = 0,25 значение функции B (t) соответствует четверти расстояния между точками P 0 и P 1. Параметр t изменяется от 0 до 1, а B (t) описывает отрезок прямой между точками P 0 и P 1.
|
[править]Квадратичные кривые
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q 0 и Q 1 из условия чтобы параметр t изменялся от 0 до 1:
§ Точка Q 0 изменяется от P 0 до P 1 и описывает линейную кривую Безье.
§ Точка Q 1 изменяется от P 1 до P 2 и также описывает линейную кривую Безье.
§ Точка B изменяется от Q 0 до Q 1 и описывает квадратичную кривую Безье.
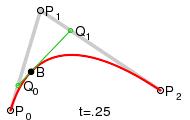Построение квадратичной кривой Безье
| 
Анимация t: [0; 1]
|
[править]Кривые высших степеней
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q 0, Q 1 и Q 2, описывающие линейные кривые, а также точки R 0 и R 1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0
Построение кубической кривой Безье
| 
Анимация t: [0; 1]
|
Для кривых четвёртой степени это будут точки Q 0, Q 1, Q 2 и Q 3, описывающие линейные кривые, R 0, R 1 и R 2, которые описывают квадратичные кривые, а также точки S 0и S 1, описывающие кубические кривые Безье:
Построение кривой Безье 4-й степени
| 
Анимация t: [0; 1]
|
[править]Свойства кривой Безье
§ непрерывность заполнения сегмента между начальной и конечной точками;
§ кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
§ при наличии только двух контрольных точек сегмент представляет собой прямую линию;
§ прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
§ кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
§ масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна»;
§ изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
§ степень кривой всегда на одну ступень ниже числа контрольных точек. Например, при трех контрольных точках форма кривой — парабола;
§ окружность не может быть описана параметрическим уравнением кривой Безье;
§ невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).
[править]Применение в компьютерной графике
Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path).
9. Цифровой дифференциальный анализатор
специализированная цифровая интегрирующая машина, основу которой составляют цифровые интегрирующие устройства (См. Интегрирующее устройство) (интеграторы), выполняющие интегрирование по независимой переменной, задаваемой в виде приращений (представленных в двоичной или троичной системе счисления). Решение задачи в Ц. д. а. определяется взаимодействием интеграторов, организуемых так же, как это делается в схемах набора задач в аналоговой вычислительной машине (См. Аналоговая вычислительная машина) (АВМ). Ц. д. а. занимает промежуточное положение между АВМ и ЦВМ: по способам подготовки и методам решения задач Ц. д. а. имеют много общего с АВМ, а по формам представления данных и используемым элементам — с ЦВМ.
Ц. д. а. по сравнению с АВМ обладают более высокой точностью вычислений, но меньшими быстродействием и универсальностью; они могут выполнять интегрирование по любой независимой переменной, а АВМ — только по времени. Ц. д. а. не могут решать сложных логических задач, как ЦВМ. Изменение переменных в Ц. д. а. определяется накоплением приращений, вследствие чего быстродействие Ц. д. а. обратно пропорционально обеспечиваемой точности вычислений: чем выше требуемая точность, тем меньше должна быть величина каждого элементарного приращения и соответственно ниже быстродействие.
Ц. д. а. делятся на последовательные и параллельные. В последовательных Ц. д. а. интегрирование осуществляется за счёт многократного использования одного физически реализованного интегратора и запоминания результата интегрирования. Такие Ц. л. а. относительно просты и недороги. В параллельных Ц. л. а. все интеграторы работают одновременно; такие Ц. д. а. сложнее и дороже последовательных, но обеспечивают более высокое быстродействие.