Задачи изучения дисциплины. 2 глава

Для традиционных направлений исследований проблема обоснования состава показателей обычно считается решенной. Например, в макроэкономических исследованиях производительности труда, обычно рассматриваются регламентированные, уже устоявшиеся наборы показателей, значения которых публикуются в статистических сборниках, научных отчетах и других официальных издания Госкомстата. Такие как выработка на одного работающего как показатель, выражающий явление «производительность труда», объемы ВВП ‑ показатель результативности экономики), объемы основных фондов ‑ показатель уровня материальной обеспеченности производственного процесса, экономики) и ряд других.

Вместе с тем в ряде областей эконометрических исследований такие системы показателей не могут быть сформированы столь однозначно. Часто одно и то же явление может быть выражено альтернативными вариантами показателей.

В отсутствие объективных данных в эконометрических исследованиях допускается замена одного показателя другим, косвенно отражающим то же явление. Например, среднедушевой доход как показатель материального уровня жизни может быть заменен среднегодовым товарооборотом на одного жителя региона. Неправильный выбор показателя, представляющего рассматриваемое явление в модели, может существенно повлиять на качество эконометрической модели.

 

2.2. Выбор факторов эконометрической модели

 

Проблема обоснования «оптимального» набора факторов обычно решается на основе как содержательного (теоретического), так и количественного (статистического) анализа тенденций рассматриваемых процессов.

На этапе содержательного анализа решается вопрос о целесообразности включения в модель тех или иных факторов, исходя из их экономического смысла. В макроэкономических исследованиях состав факторов, как правило, определяется на основании допущений экономической теории. Пример — двухфакторные производственные функции типа Кобба-Дугласа, которые строятся в предположении, что объем выпуска (производства) экономической системы в основном зависит от размеров используемых основных фондов и количества затраченного труда. Функция типа Кобба-Дугласа учитывает теоретическое предположение о постоянной эластичности выпуска по каждому из производственных факторов.

На этапе содержательного анализа обычно решается проблема установления самого факта наличия взаимосвязей между явлениями. Однако каждое из явлений может быть представлено разными наборами факторами и даже их комбинациями. Поэтому в ряде исследований на основании содержательного анализа однозначно состав независимых переменных модели определить практически невозможно. Могут существовать их альтернативные наборы.

Например, для исследования закономерностей динамики производительности труда на заводе могут быть отобраны следующие факторы: объем основных фондов, энерговооруженность труда, фондовооруженность труда, численность рабочей силы, ее квалификация. При этом квалификация как явление может выражаться разными показателями, например, средним уровнем образования работников, их усредненным квалификационным разрядом и т.п. Кроме того, можно ожидать, что показатели энерговооруженности, фондовооруженности труда, объема основных фондов характеризуют одно и то же явление — уровень материально-технической оснащенности производственного процесса. Таким образом, некоторые из рассматриваемых в таком исследовании показателей, выражающих количественные характеристики независимых переменных, относятся к сходным явлениям.

Факторы, выражающие одну и ту же причину, могут быть тесно взаимосвязаны между собой. Так, уровень розничного товарооборота в основном зависит от среднедушевого дохода; концентрация загрязняющих веществ — от объемов их выбросов. Вследствие этого одновременное включение таких факторов в модель вряд ли целесообразно, поскольку, таким образом, одна и та же причина будет учтена дважды. В результате в общем случае на этапе обоснования эконометрической модели решается задача выбора наиболее предпочтительного состава независимых факторов среди ряда альтернативных вариантов.

Можно выделить два основных подхода к решению этой проблемы. Первый предполагает априорное (до построения модели) исследование характера и силы взаимосвязей между рассматриваемыми переменными, по результатам которого в модель включаются факторы, наиболее значимые по своему «непосредственному» влиянию на зависимую переменную у. И, наоборот, из модели исключаются факторы, которые, либо малозначимы с точки зрения силы своего влияния на эту переменную, либо их сильное влияние на нее обусловлено индуцированными взаимосвязями с другими переменными.

В основе «априорного» подхода лежат следующие предположения.

1. Сильное влияние фактора на зависимую переменную должно подтверждаться определенными количественными характеристиками, важнейшей является их парный линейный коэффициент корреляции, выборочное значение которого рассчитывается на основании имеющейся информации.

Логика использования коэффициента парной корреляции при отборе значимых факторов на практике состоит в следующем. Если значение коэффициента корреляции достаточно велико, т.е. превосходит некоторый эмпирический рубеж (на практике 0,5-0,6), то можно говорить о наличии существенной линейной связи между переменными у и X_i, или о достаточно сильном влиянии X_i на у. Чем больше абсолютное значение r_{yx i}, тем сильнее это влияние (положительное или отрицательное, в зависимости от знака коэффициента парной корреляции).

2. Если два и более факторов выражают одно и то же явление, то, как правило, между ними также должна существовать достаточно сильная взаимосвязь. На это может указать выборочное значение их парного коэффициента корреляции. На практике взаимосвязь между факторами признается существенной, если их коэффициент корреляции достигает величины 0,8-0,9. В таких ситуациях один из этих факторов целесообразно исключить из модели, чтобы одна и та же причина не учитывалась дважды. Однако такое исключение следует проводить только в тех случаях, когда факторы выражают одно и то же явление.

Приведенные рубежные значения (в первом случае — 0,5-0,6; во втором — 0,8-0,9) достаточно условны. В каждом конкретном случае они устанавливаются индивидуально. Значительно усложняет проблему отбора факторов явление ложной корреляции, которое характеризуется достаточно высокими по абсолютной величине значениями коэффициентов парной корреляции с содержательной точки зрения между собой никак не связанных факторов. Иными словами, большие значения парных коэффициентов корреляции могут иметь место и в тех случаях, когда тенденции рассматриваемых процессов совпали случайно, при отсутствии между ними взаимосвязи, обоснованной представлениями соответствующей экономической теории.

Ложная корреляция может помешать при построении «правильной» модели по двум причинам. Во-первых, в модель случайно могут быть введены незначимые с содержательной точки зрения факторы, характеризующиеся значимыми величинами коэффициента парной корреляции. Во-вторых, из модели могут быть исключены значимые с точки зрения влияния на у факторы, в отношении которых ошибочно признана гипотеза о том, что они выражают то же явление, что и другой фактор (факторы), уже включенный в эту модель.

Среди основных причин включения в модель переменных с ложной корреляцией часто называют ненадежность информации, используемой при определении значений факторов в различные моменты времени, трудности формализации факторов, имеющих качественный характер, неустойчивость тенденций изменения рассматриваемых переменных, неправильную форму взаимосвязи между ними и т.п. Основной путь, придерживаясь которого можно избежать ошибок, связанных с понятием «ложной корреляции», связан с проведением качественного анализа проблемы, направленного на обоснование адекватного ей содержания и формы модели.

Второй подход к отбору независимых факторов — можно назвать апостериорным — предполагает первоначально включить в модель все отобранные на этапе содержательного анализа факторы. Уточнение их состава в этом случае производится на основе анализа характеристик качества построенной модели и силы влияния каждого из факторов на зависимую переменную.

Если фактор X_i признается незначимым, его целесообразно удалить из модели. Эта операция приводит к уменьшению общего количества независимых переменных в модели. Таким образом, на практике используют следующую поэтапную процедуру построения окончательного варианта модели на основе апостериорного подхода:

1. В исходный вариант модели включаются все факторы, отобранные в ходе содержательного анализа проблемы. Рассчитывают значения оценок коэффициентов модели, их среднеквадратические ошибки и значения критериев Стьюдента.

2. Из модели удаляют незначимый фактор, характеризующийся наименьшим значением критерия Стьюдента, при условии, что он статистически незначим и формируют новый вариант модели с уменьшенным на один числом факторов.

Заметим, что в модели может быть несколько незначимых факторов. Однако все их одновременно удалять не следует. Возможно, что недостаточная значимость большинства факторов обусловлена влиянием «наихудшего» из незначимых факторов и на следующем шаге расчетов они окажутся значимыми.

3. Процесс отбора факторов считают законченным, когда остающиеся в модели факторы являются значимыми, если полученный вариант модели удовлетворяет и другим критериям ее качества, то процесс построения модели можно считать завершенным в целом.

В противном случае попытаются сформировать другой альтернативный вариант модели, отличающийся от предыдущего либо составом факторов, либо формой их взаимосвязи с зависимой переменной.

Каждый из этих подходов имеет свои преимущества и недостатки. «Априорный» путь отбора факторов не обладает достаточной обоснованностью. Он в большей степени использует «прямые» количественные индикаторы «силы» взаимосвязей между рассматриваемыми величинами и не принимает во внимание в полной мере особенности комплексного влияния независимых факторов на переменную у т.е. своеобразные эффекты «эмерджентности» такого влияния.

Этот эффект выражается в том, что совокупное воздействие нескольких факторов на переменную у, может значительно отличаться от суммы воздействий каждого из них именно в силу наличия внутренних взаимосвязей между независимыми переменными. Вместе с тем использование априорного подхода часто позволяет уточнить некоторые предварительные альтернативные варианты наборов независимых факторов, проверить исходные предпосылки модели относительно правильности выбора формы взаимосвязей между ними.

«Апостериорный» подход к отбору факторов, на первый взгляд, предпочтительнее из-за того, что целесообразность включения в модель каждого из факторов определяется на основании всего комплекса взаимосвязей между переменными. Однако когда общее количество факторов достаточно велико, нет никаких гарантий того, что множество несущественных, а то и ложных взаимосвязей между ними не будет превалировать над основными связями. В результате может оказаться, что в числе первых кандидатов на исключение будут «названы» наиболее важные, значимые с точки зрения влияния на переменную у, факторы. Поэтому в сложных случаях, т.е. при наличии большого числа отобранных для включения в модель на этапе содержательного анализа факторов, полезно сочетать при обосновании их «оптимального» состава оба подхода, как априорный, так и апостериорный.

3. Множественная линейная регрессия

 

Множественный регрессионный анализ является расширением парного регрессионного анализа. О применяется в тех случаям, когда поведение объясняемой, зависимой переменной необходимо связать с влиянием более чем одной факторной, независимой переменной. Хотя определенная часть многофакторного анализа представляет собой непосредственное обобщение понятий парной регрессионной модели, при выполнении его может возникнуть ряд принципиально новых задач.

Так, при оценке влияния каждой независимой переменной необходимо уметь разграничивать ее воздействие на объясняемую переменную от воздействия других независимых переменных. При этом множественный корреляционный анализ сводится к анализу парных, частных корреляций. На практике обычно ограничиваются определением их обобщенных числовых характеристик, таких как частные коэффициенты эластичности, частные коэффициенты корреляции, стандартизованные коэффициенты множественной регрессии.

Затем решаются задачи спецификации регрессионной модели, одна из которых состоит в определении объема и состава совокупности независимых переменных, которые могут оказывать влияние на объясняемую переменную. Хотя это часто делается из априорных соображений или на основании соответствующей экономической (качественной) теории, некоторые переменные могут в силу индивидуальных особенностей изучаемых объектов не подходить для модели. В качестве наиболее характерных из них можно назвать мультиколлинеарность или автокоррелированность факторных переменных.

 

3.1. Анализ множественной линейной регрессии с помощью

метода наименьших квадратов (МНК)

 

В данном разделе полагается, что рассматривается модель регрессии, которая специфицирована правильно. Обратное, если исходные предположения оказались неверными, можно установить только на основании качества полученной модели. Следовательно, этот этап является исходным для проведения множественного регрессионного анализа даже в самом сложном случае, поскольку только он, а точнее его результаты могут дать основания для дальнейшего уточнения модельных представлений. В таком случае выполняются необходимые изменения и дополнения в спецификации модели, и анализ повторяется после уточнения модели до тех пор, пока не будут получены удовлетворительные результаты.

На любой экономический показатель в реальных условиях обычно оказывает влияние не один, а несколько и не всегда независимых факторов. Например, спрос на некоторый вид товара определяется не только ценой данного товара, но и ценами на замещающие и дополняющие товары, доходом потребителей и многими другими факторами. В этом случае вместо парной регрессии M(Y/_{Х = х}) = f(x) рассматривается множественная регрессия

M(Y/_{Х1 = х1, Х2 = х2, …, Хр = Хр}) = f(x₁, х₂, …, х_р) (2.1)

 

Задача оценки статистической взаимосвязи переменных Y и Х₁, Х₂,..., Х_Р формулируется аналогично случаю парной регрессии. Уравнение множественной регрессии может быть представлено в виде

Y = f (B, X) + e (2.2)

где X — вектор независимых (объясняющих) переменных; В — вектор параметров уравнения (подлежащих определению); e - случайная ошибка (отклонение); Y — зависимая (объясняемая) переменная.

Предполагается, что для данной генеральной совокупности именно функция f связывает исследуемую переменную Y с вектором независимых переменных X.

Рассмотрим самую употребляемую и наиболее простую для статистического анализа и экономической интерпретации модель множественной линейной регрессии. Для этого имеются, по крайней мере, две существенные причины.

Во-первых, уравнение регрессии является линейным, если система случайных величин (X₁, X₂,..., Х_Р, Y) имеет совместный нормальный закон распределения. Предположение о нормальном распределении может быть в ряде случаев обосновано с помощью предельных теорем теории вероятностей. Часто такое предположение принимается в качестве гипотезы, когда при последующем анализе и интерпретации его результатов не возникает явных противоречий.

Вторая причина, по которой линейная регрессионная модель предпочтительней других, состоит в том, что при использовании ее для прогноза риск значительной ошибки оказывается минимальным.

Теоретическое линейное уравнение регрессии имеет вид:

, (2.3)

или для индивидуальных наблюдений с номером i:

(2.4)

где i = 1, 2,..., п.

Здесь В = (b ₀, b ₁,, b _Р) — вектор размерности (р+1) неизвестных параметров b_j, j = 0, 1, 2,..., р, называется j -ым теоретическим коэффициентом регрессии (частичным коэффициентом регрессии). Он характеризует чувствительность величины Y к изменению X_j. Другими словами, он отражает влияние на условное математическое ожидание M(Y/_{Х1 = х1, Х2 = х2, …, Хр = xр}) зависимой переменной Y объясняющей переменной Х _j при условии, что все другие объясняющие переменные модели остаются постоянными. b ₀ — свободный член, определяющий значение Y в случае, когда все объясняющие переменные X_j равны нулю.

После выбора линейной функции в качестве модели зависимости необходимо оценить параметры регрессии.

Пусть имеется n наблюдений вектора объясняющих переменных X = (1, X₁, X₂,..., Х_Р) и зависимой переменной Y:

(1, х_i1, x_i2, …, x_ip, y_i), i = 1, 2, …, n.

Для того чтобы однозначно можно было бы решить задачу отыскания параметров b ₀, b ₁, …, b _Р (т.е. найти некоторый наилучший вектор В), должно выполняться неравенство n > p + 1. Если это неравенство не будет выполняться, то существует бесконечно много различных векторов параметров, при которых линейная формула связи между X и Y будет абсолютно точно соответствовать имеющимся наблюдениям. При этом, если n = p + 1, то оценки коэффициентов вектора В рассчитываются единственным образом — путем решения системы p + 1 линейного уравнения:

(2.5)

где i = 1, 2,..., п.

Например, для однозначного определения оценок параметров уравнения регрессии Y = b о + b ₁ X ₁ + b ₂ X ₂ достаточно иметь выборку из трех наблюдений (1, х _i1, х _i2, y _i), i = 1, 2, 3. В этом случае найденные значения параметров b ₀, b ₁, b ₂ определяют такую плоскость Y = b о + b ₁ X ₁ + b ₂ X ₂ в трехмерном пространстве, которая пройдет именно через имеющиеся три точки.

С другой стороны, добавление в выборку к имеющимся трем наблюдениям еще одного приведет к тому, что четвертая точка (х ₄₁, х ₄₂, х ₄₃, y ₄) практически всегда будет лежать вне построенной плоскости (и, возможно, достаточно далеко). Это потребует определенной переоценки параметров.

Таким образом, вполне логичен следующий вывод: если число наблюдений больше минимально необходимой величины, т.е. n > p + 1, то уже нельзя подобрать линейную форму, в точности удовлетворяющую всем наблюдениям. Поэтому возникает необходимость оптимизации, т.е. оценивания параметров b ₀, b ₁, …, b_Р, при которых формула регрессии дает наилучшее приближение одновременно для всех имеющихся наблюдений.

В данном случае число n = n - p - 1 называется числом степеней свободы. Нетрудно заметить, что если число степеней свободы невелико, то статистическая надежность оцениваемой формулы невысока. Например, вероятность надежного вывода (получения наиболее реалистичных оценок) по трем наблюдениям существенно ниже, чем по тридцати. Считается, что при оценивании множественной линейной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений превосходило число оцениваемых параметров, по крайней мере, в 3 раза.

Прежде чем перейти к описанию алгоритма нахождения оценок коэффициентов регрессии, отметим желательность выполнимости ряда предпосылок МНК, которые позволят обосновать характерные особенности регрессионного анализа в рамках классической линейной многофакторной модели.

 

3.2. Теоретические предпосылки МНК

 

1°. Математическое ожидание случайного отклонения e_i равно нулю для всех наблюдений:

2°. Наличие гомоскедастичности (постоянство дисперсии случайных отклонений). Дисперсия случайных отклонений e_i должна быть постоянной:

D(e_i) = D(e_j) = s² для любых наблюдений с номером i и j.

3°. Отсутствие автокорреляции. Случайные отклонения e_i и e_j не должны зависеть друг от друга для всех i j.

4°. Случайное отклонение должно быть независимым от объясняющих переменных:

.

5°. Модель эмпирической регрессии должна являться линейной относительно параметров. Это ограничение не распространяется на факторные переменные.

6°. Отсутствие мультиколлинеарности. Между объясняющими переменными должна отсутствовать строгая (сильная) линейная зависимость.

7°. Случайные величины ‑ошибки e_i, i = 1, 2,..., п, должны иметь нормальный закон распределения (e_i ~ N(0, s_e )).

Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.

Как и в случае парной регрессии, истинные значения параметров b_j с помощью случайной выборки получить невозможно. В этом случае вместо теоретического уравнения регрессии (2.3) оценивается так называемое эмпирическое уравнение регрессии. Эмпирическое уравнение регрессии представим в виде:

(2.6)

Здесь — оценки теоретических значений b₀, b₁,..., b_p коэффициентов регрессии (эмпирические коэффициенты регрессий); е — эмпирическая оценка неизвестного случайного отклонения e. Для индивидуальных наблюдений имеем:

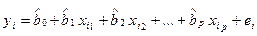(2.7)

Оцененное уравнение в первую очередь должно описывать общую закономерную тенденцию изменения зависимой переменной Y. При этом необходимо иметь возможность оценить случайные отклонения измеренных значений y_i от таких неслучайных расчетных значений.

По данным выборки объема п: (1, х_i1, x_i2,..., x_ip, y_i), i = 1, 2,..., п, требуется оценить значения параметров b_j вектора B, т.е. провести параметризацию выбранной модели (здесь х_ij, j = 0, 1, 2,..., p значение переменной Xj в i -oм наблюдении).

При выполнении перечисленных выше предпосылок МНК относительно ошибок e_i оценки коэффициентов b₀, b₁,..., b_p множественной линейной регрессии с помощью МНК являются несмещенными, эффективными и состоятельными (т.е. BLUE-оценками).

На основании (5.7) отклонение e_i значения зависимой переменной Y от модельного значения , соответствующего уравнению регрессии в i -oм наблюдении (i = 1, 2,..., n), рассчитывается по формуле:

(2.8)

Наиболее распространенным методом оценки параметров уравнения множественной линейной регрессии является метод наименьших квадратов (МНК). Его суть состоит в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной Y от ее расчетных значений , получаемых с помощью модельного уравнения регрессии:

 

По МНК для нахождения оценок минимизируется следующая функция, квадратичная относительно коэффициентов регрессии b₀, b₁,..., b_p:

. (2.9)

Данная функция является квадратичной относительно неизвестных величин b_j, j = 0, 1,..., p. Она ограничена снизу, следовательно, имеет минимум. Необходимым условием минимума функции S(b₀, b₁,..., b_p) является равенство нулю всех ее частных производных по b_j. Частные производные квадратичной функции (2.9) являются линейными функциям относительно искомых оценок коэффициентов регрессии:

,

, (2.10)

где j = 1, 2,..., p.

Приравнивая их к нулю, получаем нормальную систему р + 1 линейных уравнений с р + 1 неизвестными оценками коэффициентов регрессии, что является одним из достоинств метода МНК. Такая система имеет обычно единственное решение:

 

,

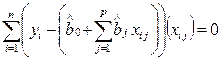, (2.11)

где j = 1, 2,..., p.

В исключительных случаях, когда столбцы системы линейных уравнений линейно зависимы, она имеет бесконечно много решений или не имеет решения вовсе. Однако данные реальных статистических наблюдений к таким исключительным случаям практически никогда не приводят.

Система линейных уравнений относительно неизвестных оценок параметров линейной модели имеет следующий вид:

После деления всех уравнений системы на объем выборки n все суммарные величины преобразуются в соответствующие средние величины:

(2.12)

Из первого уравнения можно определить величину коэффициента регрессии :

Подставляя его в уравнение (2.8), получим следующую форму записи эмпирического линейного уравнения множественной регрессии:

Нормальную систему линейных уравнений МНК (2.11) наиболее наглядно можно представить с помощью векторно-матричной формы записи.

 

3.3. Оценивание коэффициентов множественной

линейной регрессии

 

Представим данные наблюдений и соответствующие коэффициенты в матричной форме.

Здесь Y — n - мерный вектор-столбец наблюдений зависимой переменной Y; X — матрица размерности п х (p + 1), в которой i - я строка (i = 1, 2,..., п) представляет наблюдение вектора значений независимых переменных X₁, X₂,..., Х_Р; единица соответствует переменной при свободном члене b_o, В — вектор-столбец размерности (p+1) параметров уравнения регрессии (2.8); е — вектор-столбец отклонений выборочных (реальных) значений y_i зависимой переменной Y (2.7) от значений , размерности п,получаемых из модельного уравнения регрессии:

(2.14)

Сумма квадратов отклонений МНК в матричном виде запишется следующим образом:

Условие экстремума: . (2.15)

Частные производные по параметрам в матричной форме вычисляются следующим образом: