Модели дожития и таблицы смертности
Вычисление приведенных стоимостей в страховании жизни
Вычисление премий
Вычисление резервов
Расторжение договора и изменение условий договора страхования.
Моделирование финансовых потоков. Тестирование доходности.
Система международных актуарных обозначений.
Основная функция актуария – оценивать соответствие активов принимаемым обязательствам. Они отвечают на вопрос, какими резервами должен обладать страховщик, чтобы не терпеть убытки, и, исходя из этого, рассчитывают тарифы. В их распоряжении инструментарий математической статистики и теории вероятности. По сути, от навыков и знаний этих специалистов зависит устойчивость всей страховой системы.
Классификация актуарных расчетов[6]


Элементы финансовой математики
1.1. Процент, дисконт и ставка дисконтирования. Простой, сложный, переменный процент. Эффективная ставка процента. Номинальная ставка процента.
1.2. Непрерывное начисление процентов.
1.3. Анализ детерминированных финансовых потоков. Накопленная, приведенная и современная стоимость.
1.4. Методы вычисления процентной ставки: усреднение по стоимости, усреднение по времени. Учет инфляции.
1.5. Расчет финансовых рент.
Временная ценность денег
В условиях рыночной экономики при проведении финансовых операций важнейшую роль играет фактор времени. "Золотое" правило бизнеса гласит[7]:
Сумма, полученная сегодня, больше той же суммы, полученной завтра
В финансовом менеджменте учет фактора времени осуществляется с помощью методов наращения и дисконтирования, в основу которых положена техника процентных вычислений.
С помощью этих методов осуществляется приведение денежных сумм, относящихся к различным временным периодам, к требуемому моменту времени в настоящем или будущем. При этом в качестве нормы приведения используется процентная ставка [interest rate – i].
Опр. В узком смысле процентная ставка представляет собой цену, уплачиваемую за использование заемных денежных средств.
Опр. Под наращением понимают процесс увеличения первоначальной суммы в результате начисления процентов.
Экономический смысл метода наращения состоит в определении величины, которая будет или может быть получена из некоторой первоначальной (текущей) суммы в результате проведения операции. Другими словами, метод наращения позволяет определить будущую величину [future value – FV] текущей суммы [present value – PV] через некоторый промежуток времени, исходя из заданной процентной ставки i.
Опр. Дисконтирование представляет собой процесс нахождения величины на заданный момент времени по ее известному или предполагаемому значению в будущем.
В экономическом смысле величина PV, найденная в процессе дисконтирования, показывает современное (с позиции текущего момента времени) значение будущей величины FV.
Дисконтирование, по сути, является зеркальным отражением наращения. Используемую при этом процентную ставку d называют нормой дисконта.
В зависимости от условий проведения финансовых операций, как наращение, так и дисконтирование, могут осуществляться с применением простых, сложных либо непрерывных процентов.
Процентные ставки
В финансовом менеджменте процентную ставку используют в качестве измерителя уровня (нормы) доходности производимых операций, исчисляемого как отношение полученной прибыли к величине вложенных средств.
Опр. Проценты (процентные деньги) - это абсолютная величина дохода от предоставления капитала в долг в любой ее форме (выдача ссуды, покупка облигации, учет векселя, продажа товара в кредит и т.д.)[8].
Опр. Процентная ставка (i) – это отношение суммы процентных денег (I), выплачиваемых за фиксированный отрезок времени, к величине вклада (P). Определяется по формуле:

где I - сумма процентов;
P - сумма капитала, предоставляемого в кредит;
i - процентная ставка, может быть выражена в виде десятичной или обыкновенной дроби и уточняется в договоре с точностью до  и даже
и даже  .
.
Проценты либо выплачиваются кредитору по мере их начисления, либо присоединяются к сумме долга.
Опр. Наращением первоначальной суммы вкладываемого капитала (FV) называется процесс её увеличения за счет присоединения процентных денег (I) к основному капиталу (FV):
FV = PV + I.
Опр. Период начисления - это промежуток времени, за который начисляются проценты (n).
В зависимости от условий договора, период начисления может быть разбит на интервалы, по прошествии которых происходит начисление процентов.
| Процентные ставки | |||
| Способы начисления процентных ставок | Виды процентных ставок | ||
| декурсивный (постоянный или фиксированный) | антисипативный (переменные или плавающие) | простые | сложные |
| Проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из предоставляемого капитала P. Процентная ставка представляет собой отношение суммы начисленного за определенный интервал дохода (процентов) к сумме имеющегося капитала на начало данного интервала. | Проценты начисляются в начале каждого интервала. Сумма процентных денег (дохода) определяется исходя из наращенной суммы. В этом случае процентная ставка представляет собой отношение суммы дохода, выплачиваемой за определенный интервал, к величине наращенной суммы. Такая процентная ставка называется учетной (в широком смысле). В договоре указывается изменяющаяся во времени базовая ставка (база) и размер надбавки к ней (маржи)[9]. | Ставки процентов применяются к одной и той же начальной сумме на протяжении всего срока ссуды | Ставки процентов применяются к сумме с начисленными в предыдущем периоде процентами |
Простые проценты
Как правило, простые проценты используются в краткосрочных финансовых операциях, срок проведения которых меньше года. Базой для исчисления процентов за каждый период в этом случае является первоначальная (исходная) сумма сделки.
Величина годовой процентной ставки определяется как

где IГ - сумма процентов за год;
PV - сумма первоначального капитала
i – годовая процентная ставка, выраженная десятичной дробью.
Для простых процентов доход (interest) за n лет составит:
 .
.
В общем случае, наращение по ставке простых процентов осуществляют по следующим формуле:

Процесс изменения суммы капитала с начисленными простыми процентами определения арифметической прогрессией (рисунок 1):

Рисунок 1.
Задача
Юридическое лицо взяло кредит в банке в размере 100 000 руб. на срок 1,5 года при ставке простых процентов, равной 18% годовых. Определить начисленные проценты и сумму долгана конец срока.
Решение:
1)  - проценты за 1,5 года.
- проценты за 1,5 года.
2)  - должно заплатить юридическое лицо в конце срока.
- должно заплатить юридическое лицо в конце срока.
Ответ: I = 27 000 руб. FV = 127 000руб.
Задача
Клиент поместил на депозитный счет 30 000 руб., срок долга 3 года при ставке простых процентов, равной 6,2% годовых. Определить начисленные проценты и наращение на конец срока.
Решение:
1)  - проценты за 3 года.
- проценты за 3 года.
2)  получит клиент через 3 года.
получит клиент через 3 года.
Ответ: I = 5580 руб. FV = 35 580руб.
Выбор временной базы
Формулу наращения можно переписать: 
Опр. Коэффициентом наращения (kН) называется безразмерная величина, которая показывает, во сколько раз вырос капитал:  .
.
На практике продолжительность краткосрочной операции обычно меньше года. В этом случае, срок проведения операции корректируется следующим образом:
 ,
,
где ¶ - число дней функционирования сделки;
К - число дней в году (временная база 360, 365 или 366).
В этом случае формула наращенной суммы примет вид:
 .
.
При определении продолжительности проведения операции, датой ее начала и окончания считаются за 1 день.
В процессе проведения анализа в качестве временной базы часто удобно использовать условный или финансовый год, состоящий из 360 дней (12 месяцев по 30 дней). Исчисляемые по такой базе проценты называют обыкновенными или коммерческими.
Точные проценты получают при базе равной фактическому числу дней в году, т.е. при К = 365 или 366.
| Варианты расчета процентов с различным выбором временной базы[10] | ||
| Точный процент с точным числом дней ссуды (британская практика) | Обыкновенные (коммерческие) проценты K=360 дням | |
| К = 365/366 (не високосный или високосный год) | с точным числом дней ссуды (французская практика) | с приближенным числом дней ссуды (германская практика) |
| Число дней ссуды (¶) определяется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения[11] | ¶ определяется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения | год делится на 12 месяцев, по 30 дней в каждом месяце |
Обыкновенные проценты (360/360) более удобно использовать в аналитических расчетах. Этим объясняется популярность их применения на практике в большинстве развитых стран, включая США и государства континентальной Европы.
В России, применяются как обыкновенные (360/360), так и точные проценты (365/365). В частности, точные проценты используются в официальных методиках ЦБР и МФ РФ для расчета доходности по государственным обязательствам. Начисление по формуле точных процентов требует определения фактического числа дней проведения операции, которое осуществляется по специальным справочным таблицам.
Обыкновенные проценты в России используются в основном при проведении операций с векселями.
Применение современных технологий позволяет реализовать любой из известных в мировой практике методов начисления процентов, освобождая аналитика от необходимости использования различных справочных материалов.
Задача
Банк выдал кредит 50 000 руб. 15 января. Срок возврата кредита 12 сентября. Процентная ставка установлена в размере 18% годовых. Год не високосный.
Определить сумму, подлежащую возврату трёмя вариантами.
Решение
Наращенную сумму долга FV, подлежащую возврату, рассчитаем тремя методами.
1)По формуле точных процентов с точным числом дней ссуды (английская практика).
Точное число дней ссуды определим по Приложению 1 «Порядковые номера дней в году». Порядковый номер 15 января -15, порядковый номер 12 сентября - 255.
Точное число дней ссуды ¶ = 255 - 14 = 241 дней.
 руб.
руб.
2)По формуле обыкновенных (коммерческих) процентов с точным числом дней ссуды (французская практика).
 руб.
руб.
3)По формуле обыкновенных процентов с приближенным числом дней ссуды (германская практика).
Приближенное число дней ссуды: январь - 16 дней, февраль, март, апрель, май, июнь, июль, август 30×7 дней, сентябрь - 12 дней.
¶ = 16 + 30×7 + 12 = 238 дней.
 руб.
руб.
Ответ: FVбрит пр = 55942,47руб.; FVфранц пр = 56025 руб.; FVгерм пр = 55950 руб.
Задача
Предприятие оформляет кредит с банком на сумму 3 000 000 руб. на срок с 5 января до 20 марта при ставке простых процентов 15% годовых. Рассчитать проценты за пользование кредитом при начислении: а) точных процентов с точным числом дней ссуды; б) обыкновенных процентов с точным числом дней ссуды; в) обыкновенных процентов с приближенным числом дней ссуды. Год високосный.
Решение
Проценты за пользование кредитом I рассчитаем тремя методами по формуле:
 .
.
а)По формуле точных процентов с точным числом дней ссуды (английская практика).
Точное число дней ссуды определим по Приложению 2 «Порядковые номера дней в году». Порядковый номер 5 января - 5, порядковый номер 20 марта - 80.
Точное число дней ссуды ¶ = 80 - 4 = 76 дней.
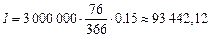 руб.
руб.
2)По формуле обыкновенных процентов с точным числом дней ссуды (французская практика).
 руб.
руб.
3)По формуле обыкновенных процентов с приближенным числом дней ссуды (германская практика).
Приближенное число дней ссуды: январь - 25 дней, февраль, март - 20 дней.
¶ = 26 + 30 + 20 = 76 дня.
 руб.
руб.
Ответ: Iбрит пр = 93 442,12руб.; Iфранц пр = 95 000,00руб.; Iгерм пр = 95 000,00руб.
Задача
За срок займа сумма обыкновенных процентов по банковскому векселю составила 15 тыс. руб. Определить сумму точных процентов при условии, что год високосный, используя прямое и обратное соотношение обыкновенных и точных процентов.
Решение

Сумма обыкновенных процентов определяется как:
 = 15 000 руб.
= 15 000 руб.
где ¶ – дни срока займа,
i – процентная ставка,
К = 360 число дней в году.
Сумма точных процентов I точ неизвестна, но может быть найдена:
 ,
,
К точ = 366 число дней в високосном году.
Тогда из соотношения:  имеем:
имеем:
 руб.
руб.
Ответ: сумма точных процентов – 14754,098 руб.
Задача
Годовая ставка Сбербанка России при начислении обыкновенных процентов по депозитному 180 - дневному сберегательному сертификату номиналом 100 000 руб. на 01.03.2010 равна 4,35 %. Год не високосный.
Определить: а) размер годовой ставки при начислении точных процентов, обеспечивающий доход, равный коммерческим процентам (двумя способами - используя прямое и обратное соотношение обыкновенных и точных процентов);
б) сумму обыкновенных и точных процентов, выплаченных при погашении сертификата.
Дано:
PV = 100 000 руб.
iобыкн = 4,32%
¶ = 180 дней
К = 365.
Найти:
а) размер годовой процентной ставки при начислении точных процентов, обеспечивающий доход, равный коммерческим процентам
б) сумму обыкновенных и точных процентов, выплаченных при погашении сертификата.
Решение
а) 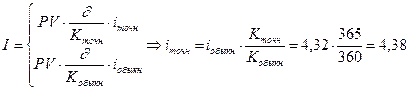 .
.
б)  руб.
руб.
 руб.
руб.
Ответ: FVобыкн = FVточн = 102 160 руб. iточн = 0,0438.