по дисциплине «МАТЕМАТИЧЕСКИЕ ОСНОВЫ ДИСКРЕТНО – ЛОГИЧЕСКИХ СИСТЕМ»

Федеральное агентство по образованию Российской Федерации

Уфимский государственный авиационный технический университет

Кумертауский филиал

 

Кафедра ЕН и ОТД

 

КУРСОВАЯ РАБОТА

по дисциплине «МАТЕМАТИЧЕСКИЕ ОСНОВЫДИСКРЕТНО – ЛОГИЧЕСКИХ СИСТЕМ»

вариант №9

 

Выполнил: ст.гр. АТПП-304

 

Проверил: ст.преподаватель

 

Оценка: _________________

Подпись: _________________

Дата: _________________

г. Кумертау

2009 г.

Федеральное агентство по образованию Российской Федерации

Уфимский государственный авиационный технический университет

Кумертауский филиал

 

 

Кафедра ЕН и ОТД

ЗАДАНИЕ

На курсовую работу по дисциплине

«Математические основы дискретных логических систем»

^{наименование дисциплине}

Студент: Группа: АТПП-304

 

1.Тема курсовой работы: Схемы из функциональных элементов с задержкой с одним входом и с одним выходом

 

2.Основное содержание:

 

 

3.Требование к оформлению:

 

3.1.Пояснительная записка должна быть оформлена в редакторе Microsoft^®Word в соответствии с требованиями ЕСКД

 

3.2. В пояснительной записке должны содержаться следующие разделы:

 

3.3. Графическая часть должна содержать:

 

Дата выдачи «01» 10.2009г. Дата окончания «_» __200_г.

 

Руководитель_____________

^{подпись}

 

Уфимский государственный авиационный технический университет

 

 

Кафедра ЕН и ОТД

 

 

100 1 2 3 4 5 6 7 8 9 10 11 12

90

 

 

 

 

 

Подпись и дата
Подпись и дата
Взоим. Инв№
Инв№ подл.
Инв№ дубл.

__________________________________________

__________________________________________

__________________________________________

Пояснительная записка

К курсовой работе по «Математическим основам дискретных логических систем»

 

4012 077209 000П3

^{(обозначение документа)}

 

Группа АТПП	Фамилия И.О.	Подпись	Дата	Оценка
Студент
Консультант
Принял

 

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КУРСОВАЯ РАБОТА

Разраб.

Провер.

Реценз.

.

Н. Контр.

Утверд.

Лит.

Листов

УГАТУ

 

 

Оглавление:

Задания на курсовую работу------------------------------------------------------------3

Оглавление-----------------------------------------------------------------------------------4

Введение--------------------------------------------------------------------------------------5

Задание 1.-------------------------------------------------------------------------------------6

Задание 2.-------------------------------------------------------------------------------------7

Задание 3.-----------------------------------------------------------------------------------10

Задание 4.-----------------------------------------------------------------------------------12

Задание 5.-----------------------------------------------------------------------------------15

Задание 6. ----------------------------------------------------------------------------------16

Задание 7. ----------------------------------------------------------------------------------19

Задание 9. ----------------------------------------------------------------------------------20

Задание 10. ---------------------------------------------------------------------------------23

Список литературы.--------------------------------------------------------------------29

 

 

Введение.

Дискре́тная матема́тика — область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах самой математики, так и в её приложениях.

К числу таких структур могут быть отнесены конечные группы, конечные графы, а также некоторые математические модели преобразователей информации, конечные автоматы, машины Тьюринга и так далее. Это примеры структур конечного (финитного) характера. Раздел дискретной математики, изучающий их, называется конечной математикой. Иногда само это понятие расширяют до дискретной математики. Помимо указанных конечных структур, дискретная математика изучает некоторые алгебраические системы, бесконечные графы, вычислительные схемы определённого вида, клеточные автоматы и т. д. В качестве синонима иногда употребляется термин «дискретный анализ».

• Математическая логика
• Математическая кибернетика
• Теория функциональных систем
• Общая алгебра
• Комбинаторика (отдельные разделы)*
• Теория графов
• Машинная арифметика
• Теория алгоритмов
• Теория игр
• Теория кодирования
• Теория конечных автоматов
• Теория множеств
• Теория формальных грамматик
• Вычислительная геометрия
• Теория булевых функций
• Логическое программирование
• Функциональное программирование
• λ-исчисление
• Булева алгебра
• Комбинаторная логика
• Математическая лингвистика
• Теория искусственного интеллекта
• Прямоугольная система линейных алгебраических уравнений

1. Доказать, что для любых трех конечных множеств А, В, С справедливо равенство, называемое формулой включения и исключения:

Пусть

Докажем (2). Очевидно, что

не пересекаются, тогда из равенства (1) получим:

О

пересекаются, тогда из равенства (1) получаем:

Теперь рассмотрим множества

Очевидно,

 

 

2. Указать все фиктивные переменные функции

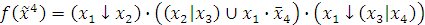
а). с помощью эквивалентных преобразований

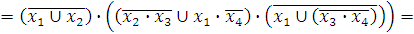
Т.к. в полученную формулу входят все исходные переменные, то -

существенные переменны, т.е. фиктивных переменных нет.

б). с помощью таблицы истинности

_{1 8 4 5 3 2 9 7 6}

 

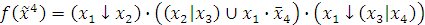
х1

х2

х3

х4

 

Проверим переменную х₁ на существенность:

рассмотрим «соседние» по переменной х₁ набор переменных. Если значения

функции на этих наборах не совпадаю, то х₁ существенная. Если же на всех

наборах значения функции будут одинаковые, то х₁ – фиктивная.

f(0₁0₁0₁0)=f(1₁0₁0₁0)

f(0₁0₁0₁1)=f(1₁0₁0₁1)

f(0₁0₁1₁0)=f(1₁0₁1₁0)

f(0₁0₁1₁1)≠f(1₁0₁1₁1)=>x₁ – существенная

Аналогично проверяются переменные х₂, х₃, х₄.

Для х₂ f(0₁0₁1₁1)≠f(0₁1₁1₁1) то х₂ – существенная

 

Для х₃ f(0₁0₁0₁1)≠f(0₁0₁1₁1) то х₃ – существенная

 

б)

Для х₄ f(0₁0₁1₁0)≠f(0₁0₁1₁1) то х₄ – существенная

 

Таким образом, фиктивных переменных для заданной формулы нет.

 

3. Используя принцип двойственности, постройте формулу, реализующию функцию, двойственную к функции f

По принципу двойственности двойственными являются дизъюнкция и

конъюнкция Т.е. для получения двойственной функции к исходной

необходимо заменить дизъюнкцию на конъюнкцию, а конъюнкцию

дизъюнкцию;

 

4. Представить в СДНФ и СКНФ следующую функцию:

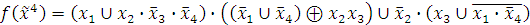
а) с помощью эквивалентных преобразований;

1:

 

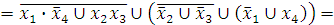
то:

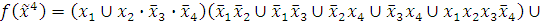
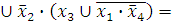
Построим СКНФ. Выпишем недостающие конъюнкции:

Заменим конъюнкцию на дизъюнкцию, «снимем» отрицания там, где они

есть, и «навесим» отрицания у тех переменных, у которых их не было.

Полученный дизъюнкт объединим конъюнкциями

 

 

6. Найти полином Жегалкина

 

а) с помощью эквивалентных преобразований;

 

б) методом неопределенных коэффициенте;

Общий вид полинома Жегалкина для функции трех переменных:

 

X1	X2	X3

 

 

 

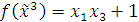
с) с помощью треугольника Паскаля.

	Треугольник Паскаля

 

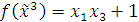
7. Проверить, является ли функция монотонной:

 

 

Т.к. на наборах (1,0,0) и (1,0,1) значения

функции , то

функция не является монотонной.

 

 

8. Найти сокращенную ДНФ функции

 

а) методом Блейка:

- сопр. ДНФ

 

б) с помощью минимизирующей карты Карно.

Построим таблицу истинности для данной функции:

 

 

Карта Карно

 

 

 

 

В карту подставляем единицы на пересечении соответствующих наборов,

для которых функция принимает значение 1.

 

Сохр. ДНФ:

 

 

9. Построить по матрице смежности наглядное изображение графа. Построить матрицу инцидентности. Найти степени вершин а и d. Построить четырехвершинный подграф. Построить дополнение к графу. Построить остов графа.

 

 

 

Матрицу инцидентности:

 

e1

e2

e3

e4

e5

e6

e7

e8

e9

e10

e11

e12

e13

e14

e15

e16

e17

e18

e19

e20

e21

e22

a

b

c

d

e

f

g

h

 

степень вершин:

deg(a)=6

deg(d)=5

 

четырехвершинный подграф.

 

 

Дополнение к графу:

 

 

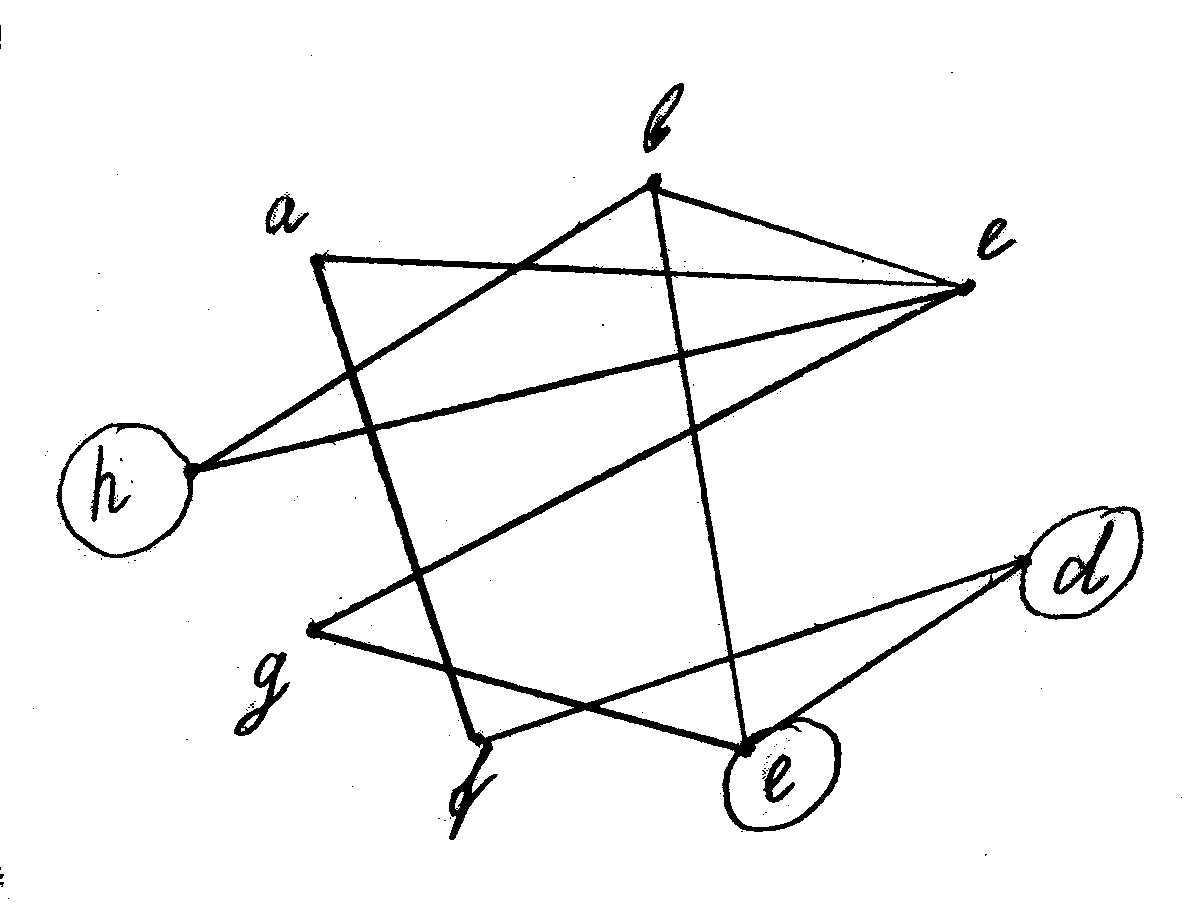
Остов графа:

 

 

 

10. Схемы из функциональных элементов с задержкой с одним входом и одним выходом.

 

При построении схем автоматов (или просто автоматов) предполагается возможным использование функциональных элементов и так называемых элементов задержки.

Элементом единичной задержки (или просто элементом задержки) называют автомат с одним входом и одним выходом (рис 1), который реализует о.-д. функцию, задаваемой системой канонических уравнений.

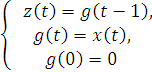
Из канонических уравнений видно, что элемент задержки представляет собой автомат с двумя состояниями, в котором сигнал, поданный на вход в момент времени t, появляется на выходе в следующий момент времени t+1(t=1,2…)

 

z(t)→ z →z(t)

рис 1

 

Возьмем произвольную о.-д.функцию f(x), задаваемой системой канонических уравнений. Построим вначале схему из функциональных элементов (конъюнкторов, дезъюнкторов и инверторов), имеющие n+l входов, l+1 выходов и реализующие булевы функции

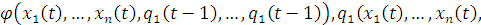
из правых частей системы. На первые n входов этой схемы подаются переменные , на последние l входов подаются

рис 2

 

 

Рис 2

 

 

 

Список литературы.

1. Нефедов В. Н., Осипова В.А. Курс дискретной математики / МАИ. М., 1992.

2. Лихтарникова Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. СПб, 1988.

3. Гиндикин С.Г. Алгебра логики в задачах. М., 1972.

4. Мамонтова Н.П. и др. Методические указания к практическим занятиям по теории сетей связи / ЛЭИС. Л., 1978.

5. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978.

6. Уилсон Р. Введение в теорию графов. М.: Мир, 1977.