Пусть функция  дифференцируема на некотором множестве
дифференцируема на некотором множестве  т.е. для всех
т.е. для всех  существует
существует  . Тогда производная
. Тогда производная  является также функцией аргумента
является также функцией аргумента  с областью определения
с областью определения  Если эта новая функция
Если эта новая функция  дифференцируема, то можно найти ее производную, называемую второй производной исходной функции
дифференцируема, то можно найти ее производную, называемую второй производной исходной функции  или производной второго порядка и обозначаемую
или производной второго порядка и обозначаемую  или
или  т.е.
т.е.

В связи с этим  для определенности называют первой производной или производной первого порядка. Ясно, что если
для определенности называют первой производной или производной первого порядка. Ясно, что если  , в свою очередь, является дифференцируемой функцией аргумента
, в свою очередь, является дифференцируемой функцией аргумента  , то последующее дифференцирование
, то последующее дифференцирование  дает третью производную
дает третью производную

и т.д. Производной n – го порядка функции  называют производную от производной (n – 1) – го порядка этой функции, т.е.
называют производную от производной (n – 1) – го порядка этой функции, т.е.
 или
или  .
.
В первой форме записи порядок производной берут в скобки, чтобы отличить от показателя степени.
Ранее было показано, что если функция имеет в точке  конечную производную, то она непрерывна в этой точке. Отсюда следует, что если функция
конечную производную, то она непрерывна в этой точке. Отсюда следует, что если функция  имеет в точке
имеет в точке  конечную производную n – го порядка, то эта функция и все ее производные до
конечную производную n – го порядка, то эта функция и все ее производные до  го порядка включительно определены в некоторой окрестности данной точки и непрерывны в указанной точке.
го порядка включительно определены в некоторой окрестности данной точки и непрерывны в указанной точке.
Функцию 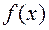 называют
называют  раз непрерывно дифференцируемой на множестве
раз непрерывно дифференцируемой на множестве  если во всех точках этого множества она имеет непрерывные производные до порядка
если во всех точках этого множества она имеет непрерывные производные до порядка  включительно.
включительно.
Введем дифференциалы высших порядков. В связи с этим дифференциал dy функции  в некоторой точке x будем называть первым дифференциалом или дифференциалом первого порядка в данной точке.
в некоторой точке x будем называть первым дифференциалом или дифференциалом первого порядка в данной точке.
Вторым дифференциалом (дифференциалом второго порядка) функции  в некоторой точке x называется дифференциал от дифференциала первого порядка в данной точке (если он существует) и обозначается
в некоторой точке x называется дифференциал от дифференциала первого порядка в данной точке (если он существует) и обозначается  Итак,
Итак,
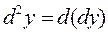
Очевидно, дифференциалом третьего порядка называется дифференциал от дифференциала второго порядка, т.е.
 и т.д.
и т.д.
Вообще, n – м дифференциалом функции  в некоторой точке x называют дифференциал в этой точке (если он существует) от дифференциала
в некоторой точке x называют дифференциал в этой точке (если он существует) от дифференциала  - го порядка в указанной точке и обозначается
- го порядка в указанной точке и обозначается  , т.е.
, т.е.
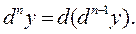
Если x – независимая переменная, то  является произвольным, не зависящим от x числом, которое при дифференцировании по x следует считать постоянным множителем. В этом случае для производной точки x имеем:
является произвольным, не зависящим от x числом, которое при дифференцировании по x следует считать постоянным множителем. В этом случае для производной точки x имеем:

Выражение  принято обозначать
принято обозначать  т.е. опускать скобки, но помнить, что это не квадрат x, а квадрат dx.
т.е. опускать скобки, но помнить, что это не квадрат x, а квадрат dx.
Аналогично 
Отсюда следует выражение для n – ой производной:

Символ в правой части можно рассматривать как отношение дифференциала n – го порядка функции к n – й степени дифференциала независимой переменной. Итак, для существования дифференциала n – го порядка функции  в точке x необходимо, чтобы эта функция была n раз дифференцируема в данной точке.
в точке x необходимо, чтобы эта функция была n раз дифференцируема в данной точке.
Для параметрически заданной функции  имеем
имеем


Примеры.
1) Найти производную 4 – го порядка от функции 
Решение. Последовательно дифференцируя функцию, получим:
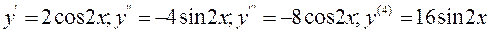
2) Найти производную второго порядка от функции, заданной параметрически: 
Решение. Последовательно дифференцируя функцию, получим:


3) Найти третий дифференциал функции 
Решение. Дифференцируя данную функцию последовательно, получим:
 Следовательно,
Следовательно, 