Основной подход при интегрировании иррациональных функций состоит в сведении искомого интеграла к интегралу от рациональной функции с помощью подходящей замены переменной (так называемая рационализация интеграла). Рассмотрим интегралы от некоторых иррациональных и трансцендентных функций.
1. Интегралы вида
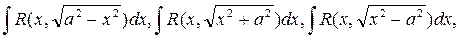
где R – рациональная функция, находятся с помощью подстановок 
соответственно.
Пример. Найти интеграл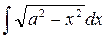 
Решение. Полагая 
получаем 
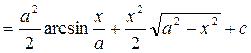, где 
Пример. Найти интеграл 
Решение. Положив 
получаем при 
2. Интегралы вида 
где 
рациональная функция, рационализируется подстановкой 
, где 
наименьшее общее кратное чисел 
Интегралы вида 
где 
рационализируется подстановкой 
где p имеет тот же смысл, что и выше.
Пример. Найти интеграл 
Решение: наименьшее общее кратное степеней 4 и 6 радикалов в подынтегральной функции равно 12.
Поэтому введем замену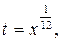 
тогда 
Получаем 
Вернемся к исходной переменной:
3. Интегрирование биномиального дифференциала (выражения вида 
).
Интеграл 
где 
рациональные числа выражаются через элементарные функции только в следующих трех случаях.
Случай 1. p – целое. Тогда, если p >0, подынтегральное выражение развертывается по формуле бинома Ньютона; если p <0, то полагаем 
где k – наименьшее общее кратное знаменателей дробей m и n.
Случай 2.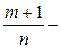 
целое. Полагаем 
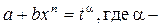знаменатель дроби p.
Случай 3. 
целое. Полагаем 
знаменатель дроби p.
В других случаях интеграл не может быть выражен в элементарных функциях.
Пример. Найти интеграл 
Решение. 
получаем 
Получаем случай 3.
Замена 
4. Интегралы вида 
где 
рациональные числа, приводятся к интегралу от биномиального дифференциала 
и потому интегрируются в элементарных функциях только в трех случаях
1) n – нечетное (
целое),
2) m – нечетное (
целое),
3) m+ n – четное (
целое).
Если число n нечетное, применяется подстановка sin x = t.
Если число m нечетное, применяется подстановка cos x = t.
Если сумма чисел m+ n – четная, применяется подстановка tg x = t
(или ctg x=t).
В частности, такая подстановка удобна для интегралов 
где n – целое положительное число. Но если m и n – неотрицательные четные числа, то удобнее метод понижения степени с помощью тригонометрических преобразований:
5. Интегралы вида 
где 
рациональная функция от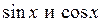 
, преобразуются в интегралы от рациональной функции подстановкой 
Эта подстановка называется универсальной. В этом случае 
В случае, когда подстановка ведет к слишком громоздким выкладкам, иногда удается использовать более простые подстановки.
Если выполняется равенство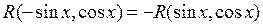 
или
то применяем подстановки 
соответственно.
Если выполняется равенство 
то применяем подстановки 
Пример. Найти интеграл 
.
Решение. 
.
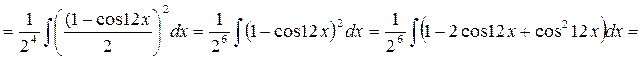
Пример. Найти интеграл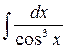 
.
Решение. Введем замену 
.
Получаем: 
.
Разложим подынтегральную функцию на простейшие дроби:
.
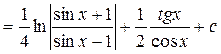Пример. Найти интеграл 
.
Решение: 
- четные, 
. Введем замену 
.
Получаем: 
.
Пример. Найти интеграл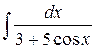 
.
Ведем замену 
.
Получаем: 
.
Определенный интеграл
Пусть функция y=f (x) задана на отрезке [ a, b ]. Разобьем отрезок [ a, b ] на п элементарных отрезков точками 
. В каждом из отрезков разбиения 
выберем произвольную точку 
и положим 
, где i=1, 2, …, n. Тогда сумма вида
(4.6)
называется интегральной суммой функции y=f (x) на отрезке [ a, b ].
Геометрический смысл величины σ показан на рис. 4.1: это сумма площадей прямоугольников с основаниями 
и высотами 
, i=1, 2, …, n.
Рис.4.1
Обозначим через λ длину максимального элементарного отрезка данного разбиения, т.е. 
.
Определение 4.3. Конечный предел I интегральной суммы σ при 
, если он существует, называется определенным интегралом от функции f (x) по отрезку [ a, b ]:
.
Определенный интеграл обозначается символом 
Если определенный интеграл существует, то функция f (x) называется интегрируемой на отрезке [ a, b ], числа а и b – соответственно нижним и верхним пределами интегрирования, f (x) – подынтегральной функцией, х – переменной интегрирования.
Теорема 4.5. (необходимое условие интегрируемости функции). Интегрируемая на [ a, b ] функция f (x) ограничена на этом отрезке.
Теорема 4.6. Если функция f (x) непрерывна на отрезке [ a, b ], то она интегрируема на нем.
Теорема 4.7. Если определенная и ограниченная на отрезке [ a, b ] функция f (x) имеет конечно число точек разрыва, то она интегрируема на этом отрезке.