Замена переменной в определенном интеграле

Теорема 4.9. Пусть: 1) f (x) – непрерывная функция на отрезке [ a, b ];

2) функция φ (t) дифференцируема на , причем непрерывна на и множеством значений функции φ (t) является отрезок [ a, b ];

3) φ (α) =а, φ (β) =b.

Тогда справедлива формула:

. (4.10)

Доказательство. Пусть F (x) – какая-либо первообразная для функции f (x) на [ a, b ]. Рассмотрим сложную функцию , так как F(x) и φ (t) дифференцируемы на соответствующих отрезках, то по правилу дифференцирования сложной функции находим

Из этого равенства следует, что функция Ф (t) является первообразной для функции , непрерывной на отрезке [ α, β ].

По формуле Ньютона-Лейбница:

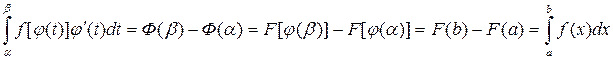Из этого равенства следует справедливость формулы (4.10), которая называется формулой замены переменной в определенном интеграле.

Замечания:

1. При вычислении определенного интеграла с помощью замены переменной не требуется возвращаться к старой переменной, как при вычислении неопределенного интеграла. При подстановке требуется сначала найти новые пределы интегрирования и выполнить необходимые преобразования в подынтегральной функции.

2. Необходимо следить за соблюдением условий теоремы 4.9.

Пример. Вычислить интеграл .

Решение. Введем замену .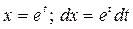

При .

Этот интеграл можно вычислить не вводя замену:

Пример. Вычислить интеграл .

Решение. Введём замену ; ; ; . При

При

Пример. Вычислить определенный интеграл .

Решение. Введем замену , тогда .

Если , то (нижний предел).

Если , то (верхний предел).

Получаем

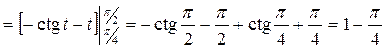
Пример. Вычислить определенный интеграл .

Решение. Введем замену (универсальная тригонометрическая подстановка).

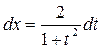При .

При

Разложим подынтегральную дробь на простейшие.

Найдем коэффициенты разложения:

Интегрирование по частям в определенном интеграле

Теорема 4.10. Пусть функции имеют непрерывные производные на отрезке Тогда справедлива формула

(4.11)

Доказательство. Поскольку функция 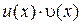является первообразной для функции то по формуле Ньютона – Лейбница

по свойству 4 определенных интегралов и вида дифференциала функции

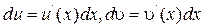
получаем, после переноса первого слагаемого в правую часть указанного равенства, формулу (4.11). (формулу интегрирование по частям в определенном интеграле). Теорема доказана.

Приведем примеры вычисления определенного интеграла по частям

Пример. Вычислить интеграл

Решение

Пример. Вычислить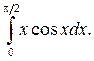

Решение.

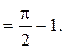
Пример. Вычислить определенный интеграл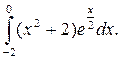

Решение

Приложение определенного интеграла. Площади плоских фигур

1. Пусть на плоскости xOy дана фигура, ограниченная отрезком оси Ox, прямыми и графиком непрерывной и неотрицательной функции на . Такую фигуру называют криволинейной трапецей (рис 4.2), площадь которой может быть вычислена по формуле

(4.12)

Рис. 4.2 Рис. 4.3.

(геометрический смысл определенного интеграла).

2. Если функция - неположительная на отрезке , то площадь S над кривой на (рис. 4.3) равна определенному интегралу

(4.10)

Замечание. Формулы (4.9) и (4.10) можно объединить в одну:

3. Если на отрезке , то площадь S фигуры, заключенной между кривыми и на этом отрезке (рис. 4.4) определяется формулой

(4.11)

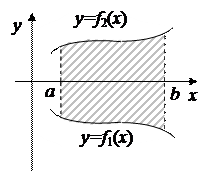Рис. 4.4. Рис. 4.5.

4. Если плоская фигура имеет более сложную форму (рис. 4.5), то прямыми, параллельными оси Oy, её следует разбить на части, чтобы можно было применить формулы (4.9) – (4.11). Тогда площадь фигуры

5. Если криволинейная трапеция ограничена кривой, заданной параметрически прямыми и осью Ox, то площадь её находится по формуле

где определяется из равенств

6. Пусть кривая MN задана в полярной системе координат уравнением где причем, функция неотрицательна на Криволинейным сектором называется плоская фигура, ограниченная кривой и лучами, направленными от полярной оси OA под углами (рис. 4.6).