ВВЕДЕНИЕ
Понятие «интеграл» непосредственно связано с интегральным исчислением − разделом математики, занимающимся изучением интегралов, их свойств и методов вычисления. Вместе с дифференциальным исчислением интегральное исчисление составляет основу математического анализа.
Так как целью курсовой работы является изучение интегрирования и дифференцирования вектор функций.
Для достижения цели необходимо решить следующие задачи:
ü Найти и изучить литературу по данной теме;
ü Изучить основные понятия вектор функции;
ü Изучить интегрирование и дифференцирование вектор функции.
Объектом исследования являются различные виды вектор функций.
В работе использованы следующие методы исследования:
1. Анализ научной литературы по теме «интегрирование и дифференцирование вектор функций»;
2. Синтез полученных знаний;
3. Обобщение полученных знаний.
Понятие вектор функции
В курсе математики и ее многочисленных приложениях часто приходится иметь дело не только с числовыми функциями, но и с функциями, у которых область определения D или множество значений E состоят из элементов другой природы, например D R, а E – подмножество множества векторов.
Векторной функцией действительного аргумента (вектор-функцией скалярного аргумента) называется отображение, которое каждому действительному числу t T R ставит в соответствие один и только один вектор трехмерного пространства R3.
Обозначается: a= a(t), t T.
Различным значениям t T соответствуют разные значения вектор-функции, т.е. векторa = a(t) имеет определенную длину (модуль) и определенное направление. Следовательно, векторa r = ar(t) может изменяться как по величине, так и по направлению.
Если каждому значению параметра  из некоторого промежутка отвечает определенный вектор
из некоторого промежутка отвечает определенный вектор  (зависящий от
(зависящий от  ), то вектор
), то вектор  называется векторной функцией (кратко вектор-функция) от скалярного аргумента
называется векторной функцией (кратко вектор-функция) от скалярного аргумента  и в этом случае пишут:
и в этом случае пишут:
 (1.1)
(1.1)
При изменении аргумента  вектор
вектор 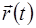 изменяется как по величине, так и по направлению. В дальнейшем будем предполагать, что
изменяется как по величине, так и по направлению. В дальнейшем будем предполагать, что  изменяется в промежутке, конечном или бесконечном.
изменяется в промежутке, конечном или бесконечном.
Будем считать, что вектор 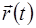 исходит из начала координат, т.е.
исходит из начала координат, т.е.  − радиус-вектор некоторой точки
− радиус-вектор некоторой точки  . В этом случае при изменении параметра
. В этом случае при изменении параметра  конец вектора
конец вектора 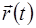 опишет линию
опишет линию  , называемую годографом векторной функции
, называемую годографом векторной функции 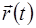 . При этом начало координат называют полюсом годографа. Уравнение (1.1) называют векторным уравнением кривой
. При этом начало координат называют полюсом годографа. Уравнение (1.1) называют векторным уравнением кривой  (рис. 1.1).
(рис. 1.1).
Если у вектора 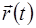 меняется только модуль, то годографом его будет луч, исходящий из полюса. Если модуль вектора
меняется только модуль, то годографом его будет луч, исходящий из полюса. Если модуль вектора 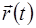 постоянен и меняется только его направление, то годограф есть линия, лежащая на сфере с центром в полюсе и радиусом, равным модулю вектора
постоянен и меняется только его направление, то годограф есть линия, лежащая на сфере с центром в полюсе и радиусом, равным модулю вектора 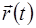 .
.

Рис. 1 Вектор - функция
Если через  обозначить проекции вектора
обозначить проекции вектора 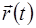 на оси прямоугольной декартовой системы координат в пространстве, то эти величины для каждого значения параметра
на оси прямоугольной декартовой системы координат в пространстве, то эти величины для каждого значения параметра  в свою очередь принимают определенные числовые значения и поэтому являются скалярными функциями скалярного аргумента
в свою очередь принимают определенные числовые значения и поэтому являются скалярными функциями скалярного аргумента  :
:
 ,
,  ,
,  . (1.2)
. (1.2)
И тогда
 . (1.3)
. (1.3)
Таким образом, задание векторной функции скалярного аргумента равносильно заданию трех скалярных функций того же аргумента. Т.к. уравнение (1.1) является уравнением некоторой кривой в пространстве, то ту же кривую задают уравнения (1.2). Уравнения (1.2) − обычные параметрические уравнения кривой в пространстве.
Предел, непрерывность, производная вектор функции
Пусть вектор-функция 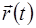 определена в окрестности точки
определена в окрестности точки  , кроме самой точки
, кроме самой точки  .
.
Вектор  называется пределом векторной функции
называется пределом векторной функции 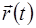 при
при  (или в точке
(или в точке  ), если
), если
 . (1.4)
. (1.4)
Если  есть предел функции
есть предел функции 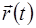 при
при  , то это записывается так
, то это записывается так
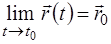 . (1.5)
. (1.5)
Если записать векторную функцию 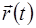 и вектор
и вектор  в проекциях
в проекциях
 ,
,
 ,
,
то получим
 .(1.6)
.(1.6)
Тогда из равенства (1.4) следует, что
 ,
,  ,
,  .(1.7)
.(1.7)
Свойства вектор-функции:
1. Если 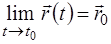 , то
, то  .
.
2.  .
.
3.  ,
,  − скалярная функция.
− скалярная функция.
4. 
5.  .
.
Вектор-функция 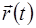 , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки  , называется непрерывной в точке
, называется непрерывной в точке  , если
, если 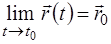 .
.
Из равносильности (1.4) и (1.7) следует, что для того чтобы вектор-функция 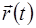 была непрерывной в точке
была непрерывной в точке  , необходимо и достаточно, чтобы в этой точке были непрерывны функции
, необходимо и достаточно, чтобы в этой точке были непрерывны функции  .
.
Введем понятие производной векторной функции
 . (1.8)
. (1.8)
Предполагаем, что начало вектора 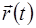 находится в начале системе координат (рис. 1.2).
находится в начале системе координат (рис. 1.2).

Возьмем фиксированное значение параметра, соответствующее какой-либо точке определенной точке  на кривой, заданной уравнением (1.8), и дадим параметру
на кривой, заданной уравнением (1.8), и дадим параметру  приращение
приращение  . Тогда получим вектор:
. Тогда получим вектор:
 ,
,
который определяет некоторую точку  . Найдем приращение вектора:
. Найдем приращение вектора:
 (1.9)
(1.9)
На рисунке, где  ,
,  . Вектор приращения определяется вектором
. Вектор приращения определяется вектором  .
.
Рассмотрим отношение  приращения вектор-функции к приращению скалярного аргумента; это есть вектор коллинеарный с вектором
приращения вектор-функции к приращению скалярного аргумента; это есть вектор коллинеарный с вектором  . При этом вектор
. При этом вектор  в сторону, соответствующую возрастанию параметра
в сторону, соответствующую возрастанию параметра  .
.
Далее с учетом (1.9) вектор  можно представить в виде
можно представить в виде
 . (1.10)
. (1.10)
Если функции  имеют производные при выбранном значении параметра
имеют производные при выбранном значении параметра  , то множители при
, то множители при  в равенстве (1.10) в пределе при
в равенстве (1.10) в пределе при  обратятся в производные
обратятся в производные  .
.
Значит,  .
.
Вектор, определяемый последним равенством, называется производной от вектора 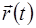 по скалярному аргументу
по скалярному аргументу  . Ее обозначают
. Ее обозначают  или
или  . Итак,
. Итак,
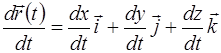 . (1.11)
. (1.11)
Выясним направление вектора  . Заметим, что при
. Заметим, что при  точка
точка  стремится к точке
стремится к точке  и поэтому секущая
и поэтому секущая 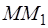 стремится к касательной в точке
стремится к касательной в точке  . Отсюда, производная
. Отсюда, производная  является вектором, касательным к годографу вектор-функции
является вектором, касательным к годографу вектор-функции 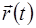 , направленным в сторону, соответствующую возрастанию параметра
, направленным в сторону, соответствующую возрастанию параметра  .
.
Из (1.11) следует, что
 . (1.12)
. (1.12)
Дифференциал длины дуги кривой равен
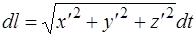 ,
,
откуда
 . (1.13)
. (1.13)
Из (1.12) и (1.13) имеем
 . (1.14)
. (1.14)
Таким образом, модуль производной вектор-функции  равен производной от длины годографа по аргументу
равен производной от длины годографа по аргументу  .
.
Правила дифференцирования вектор-функции:
1. Если  - постоянный вектор, то
- постоянный вектор, то 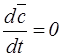 .
.
2. 
3.  , где
, где  -скалярная функция.
-скалярная функция.
4.  ,
,  скалярное произведение.
скалярное произведение.
5.  ,
,  векторное произведение.
векторное произведение.
Последовательным дифференцированием можно найти производные высших порядков
 и т.д.
и т.д.