Основные тождества (равносильные формулы) алгебры логики.

Алгебра логики (булева алгебра).

Алгебра логики. Функции алгебры логики. Таблицы истинности. Пропозициональные формулы. Равносильные формулы. Основные тождества алгебры логики. Двойственные функции. Полные системы связок. Конъюнктивные и дизъюнктивные нормальные формы. Совершенные КНФ и ДНФ. Тавтологии. Противоречия. Проблема разрешимости в алгебре логики. Логические следствия. Основные схемы доказательств.

Алгебра логики

 

Алгебраическая система (алгебра) – пара <G, M>, где G - это множество элементов (носитель), а M – множество операций, заданных на G (сигнатура).

(n-арная операция на G задаёт отображение 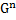на G)

 

Определение: Алгебраическая система, образованная множеством B = {0,1} вместе со всеми возможными операциями на нем, называется алгеброй логики.

Функцией алгебры логики (или логической функцией) от n переменных называется n-арная операция на В. Эта функция может принимать значения 0 или 1. (т.о. задаёт отображение B^n -> B)

Чаще всего под алгеброй логики понимают алгебру, сигнатура которой включает 3 операции: отрицание, конъюнкцию и дизъюнкцию.

Основные функции алгебры логики:

x1	u1	u2	u3	u4

Унарные:

Всего теоретически возможны 4 унарных операции, но лишь одна из них имеет собственное название и обозначение.

u3 - Отрицание: (читается: не-А)

Бинарные:

Всего существует 16 бинарных функций алгебры логики:

x1

x2

b1

b2

b3

b4

b5

b6

b7

b8

b9

b10

b11

b12

b13

b14

b15

b16

 

b2 - Конъюнкция: (читается А и В)

b8 - Дизъюнкция: (А или В)

b12 - Импликация: 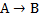(из А следует В)

Результат импликации ложен только тогда, когда исходное (А) высказывание ложно, а результат (B) истинен.

Примеры: (x делится на 4) -> (x делится на 2), Если 2*2 = 5 то 2*2 = 4

b10 - Эквиваленция: , 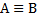(А равносильно В)

Результат эквиваленции есть истина, если A и B одновременно истины либо ложны (Иными словами, если A=B)

b7 – сложение по модулю или неравнозначность, x1Åx2

Результат сложения по модулю истинен, если истинно лишь одно из A и B (То есть, если A B)

b9 – cтрелка Пирса x1¯x2 («или-не»). Результат этой операции равносилен последовательному применению операций дизъюнкции и отрицания

b15 – штрих Шеффера обозначается x1|x2, «и-не». Результат этой операции равносилен последовательному применению операций конъюнкции и отрицания. Соответственно, результирующее высказывание будет ложным, только если входящие в него высказывания одновременно истинны. Штрих Шеффера - это операция замечательная тем, что её одной (необходимое количество раз применённой) достаточно, чтобы записать любое сложное высказывание. Является основной операцией в электронике.

Формулы алгебры логики.

Атомарные высказывания обозначаются маленькими буквами и называются пропозициональными (или булевыми) переменными. Формулы алгебры логики называются пропозициональные формулы.

Формулой является строка (знакосочетание), которая является пропозициональной переменной либо совпадает с одной из строк (), , 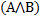(, (, (, где A и B – формулы.

Для сокращения числа скобок в формуле принято опускать скобки, не влияющие на результат. Например, вместо (x1и(x2иx3)) пишут х1их2их3 (в силу закона коммутативности).

Соглашение о порядке выполнения (приоритете, силе связывания) операций, позволяет отбросить скобки, связывающие разные операции.

Порядок выполнения логических операций следующий: сначала выполняются операции в скобках, затем операции отрицания, далее - конъюнкция, дизъюнкция, импликация, эквиваленция.

Соглашение о приоритетах операций позволяет однозначно восстановить пропущенные скобки. Например, …..

Однако, не все скобки могут быть опущены:

A -> (B -> C) А и (B или C)

(Можно тут еще про польскую запись вставить)

Таблицы истинности.

Логическое значение формулы определяется заданными логическими значениями входящих в неё элементарных высказываний.

Пример. x1=1, x2=1, x3=0. Определить значение формулы

Если же ставится задача определить все возможные значения формулы, строится таблица истинности. В этой таблице начальные столбцы соответствуют исходным (элементарным) высказываниям, а последний результирующему (сложному) высказыванию. В начальных столбцах проставляются все возможные комбинации истинности элементарных высказываний, а в последнем истинность сложного высказывания. Каждой комбинации исходных высказываний в формуле соответствует отдельная строка. Число значений формулы (и число строк таблицы) определяется числом n элементарных высказываний и равно 2^n.

x	y	Øx	Øy	xÙØy	ØÚxy	p

Пример.

Для формулы 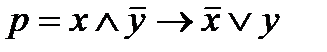построить таблицу истинности.

В нашем примере 2²=4.

 

Равносильные формулы

Две формулы алгебры логики называются равносильными, если они принимают одинаковые логические значения при любом наборе значений элементарных высказываний, входящих в формулу.

Обозначение: А=В, читается А равносильно В. Примеры: x=xÙx, xÙ0=0, xÚØx=1.

Легко видеть, что если А=В, то ØА=ØВ.

Отношение равносильности обладает следующими свойствами:

1) А=А (рефлексивно)

2) Если А=В, то В=А (симметрично)

3) Если А=В и В=С, то А=С (транзитивно)

 

Теорема об эквивалентной замене: Если формула A содержит подформулу B, и B = C, то А’=A, где А’ образованна из A заменой B на С.

 

Основные тождества (равносильные формулы) алгебры логики.

 

1. xÙy=yÙx; xÚy=yÚx – коммутативность
2. xÙ(yÙz)= (xÙy)Ùz; xÚ(yÚz)= (xÚy) Úz; - ассоциативность
3. xÙ(yÚz)=(xÙy)Ú(xÙz); xÚ(yÙz)=(xÚy)Ù(xÚz) – дистрибутивность
4. xÙx=x; xÚx=x - идемпотентность;
5. xÙ1=x; xÚ1=1; xÙ0=0; xÚ0=x – законы операций с константами
6. xÙ(yÚx)=x; xÚ(yÙx)=x – законы поглощения;
7. xÙØx=0 - закон противоречия;
8. xÚØx=1 - закон исключения третьего
9. ØØx=x – закон двойного отрицания
10. x®y = Øy®Øx – закон контрапозиции;
11. Ø(xÙy)= ØxÚØy; Ø(xÚy)=ØxÙØy – законы де Моргана;
12. (xÙy)Ú(xÙØy)=x; (xÚy)Ù(xÚØy)=x - формулы расщепления (или склеивания)

 

Все тождества можно доказать, составив таблицы истинности.

Если в тождестве заменить знак = на <-> то получится тавтология.

С помощью основных тождеств можно упрощать логические выражения, т.е. уменьшать количество формул и операций. При этом следует стремиться к замене всех связок на Ù и Ú.

Кроме перечисленных выше законов для преобразования и упрощения формул булевых функций используются тождества, получившие название правил или операций.

Правило отрицания

Для получения отрицания некоторого выражения достаточно заменить в нем знаки дизъюнкции знаками конъюнкции, знаки конъюнкции знаками дизъюнкции, а все аргументы – их отрицаниями. Если в выражении имеются константы их тоже надо заменить противоположными значениями.

Правило свертки

xÚØx Ùy=xÚy

xÙ(ØxÚy)=xÙy