Простейшие векторные поля: потенциальное, соленаидальное, гармоническое

К простейшим векторным полям относятся: соленоидальное, потенциальное и гармоническое.

Определение 1: Векторное поле называется соленоидальным или трубчатым, если во всех точках поля
Соленоидальное поле не имеет ни источников, ни стоков, его векторные линии замкнуты. Поскольку div\vec{B}=0, то поле вектора магнитной индукции является соленоидальным.

Определение 2: Векторное поле называется потенциальным или безвихревым, если во всех точках поля
Для потенциального векторного поля всегда найдется такая скалярная функция u(M) (потенциал векторного поля ), что .
Потенциал векторного поля можно найти по формуле

где 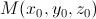– произвольная точка поля, в которой функции P, Q, R определены, С – произвольная постоянная.

Определение 3: Векторное поле называется гармоническим, если во всех точках поля и
и
т.е. поле является соленоидальным и потенциальным.
Потенциал u гармонического поля удовлетворяет уравнению Лапласа

31 Определение числового ряда, основные понятия. Необходимые и достаточные условия сходимости ряда

Пусть a1,a2,a3…a_n – числовая последовательность. Определение: Выражение вида a₁+a₂+…+a_n или a1,a2,a3…a_{n –} члены ряда an – n-й член ряба (общий член ряда) Сумма n первых членов ряда называется n-ной частичной суммой и обозначается Sn, Sn= Определение: Числовой ряд сходится, если сходится последовательность его частичных сумм, т.е. сущ-ет конечный предел при xà∞ Sn=S. Тогда S- сумма ряды Если посл-ть Sn не имеет конечного предела, то числовой ряд расходится.

Необходимое условие сходимости. Теорема: Если ряд сходится, то lim его общего члена равен 0. Док-во: Пусть S=limSn Sn=Sn-1+an, поэтому liman=lim(Sn-Sn-1) или =limSn-limSn-1=S-S=0 Следствие: (достаточное условие расходимости): Если liman≠0 то - расходится Док-во: (от противного): Пусть - сходится, тогда по теореме liman=0 – противоречие.

Свойства сходящихся числовых рядов

1°. Отбрасывание конечного числа членов не влияет на сходимость ч.р.

Рассмотрим и Пусть

тогда

(29.1)

Если существует конечный предел справа в (29.1), то существует и предел слева, и ряд сходится

2°. Если ряд сходится и имеет сумму S, то ряд

с = const, сходится и имеет сумму cS.

Пусть тогда

3°. Если ряды сходятся и имеют суммы соответственно, то ряд сходится и имеет сумму

Пусть

тогда

Необходимое условие сходимости ряда. Достаточное условие расходимости числового ряда

Необходимый признак сходимости числового ряда:

Если ряд сходится, то .

Данный признак означает, что если , то ряд расходится. Например, расходится, так как . Из выполнения условия в общем случае не следует сходимость ряда . Например, для ряда (гармонический ряд), условие выполнено, но данный ряд расходится.

Ряд u ₁ + u ₂ + u ₃ +... + u_n +... может сходиться лишь в том случае, когда член u_n (общий член ряда) стремится к нулю:

Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.