Теорема единственности предела функции в точке
3. Односторонние пределы, необходимые и достаточные условия существования предела функции в точке
4. Свойства функции, имеющей предел в точке
5. Предел функции на бесконечности
Введение
Дальнейшее изучение интегро-дифференциального счисления невозможно без понимания предела. Это понятие будет встречаться на протяжении не только всего курса высшей математики, но и на других смежных дисциплинах. Понимание материала как этой, так и последующих лекций лежит в большей части в интуитивной области, однако очень важно внимательно изучить первые два определения и понять их геометрический смысл, они являются базовыми в дальнейшем.
Определение предела функции в точке
Определение предела
Определение 1.
Число b называется пределом функции 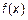 в точке
в точке  , если для любого сколь угодно малого положительного
, если для любого сколь угодно малого положительного 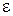 найдется другое положительное число
найдется другое положительное число  , такое, что для всех x, быть может, не равных a и удовлетворяющих неравенству
, такое, что для всех x, быть может, не равных a и удовлетворяющих неравенству  , выполняется условие
, выполняется условие  . Обозначается
. Обозначается
 . (1)
. (1)
Или то же определение с использованием сокращений 
 .
.
 Модуль
Модуль  означает, что
означает, что  , или
, или  , следовательно,
, следовательно,  . Если из
. Если из  удалить точку a, то получим проколотую дельта-окрестность (рис. 1).
удалить точку a, то получим проколотую дельта-окрестность (рис. 1).
Определение 2.

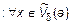
 .
.
 Из определения предела следует, что
Из определения предела следует, что 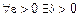
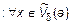 , соответственно значения функции лежат в интервале
, соответственно значения функции лежат в интервале  . Поведение функции
. Поведение функции 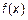 в точке
в точке  на величину предела не влияет. Функция в этой точке может быть даже не определена.
на величину предела не влияет. Функция в этой точке может быть даже не определена.
ПРИМЕР 1.
Функция  в точке
в точке  . Но
. Но  .
.
Важно!
На величину предела не влияет поведение функции в конечном числе точек дельта окрестности. Эти точки можно исключить и взять другую, меньшую дельта-окрестность.
ПРИМЕР 2.
Доказать, что  . По определению
. По определению  можно найти
можно найти 
 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , следовало бы
, следовало бы 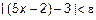 . Преобразуем неравенство в
. Преобразуем неравенство в  или
или  . Тогда для любых
. Тогда для любых  можно подобрать
можно подобрать  , то есть
, то есть  справедливо.
справедливо.
Теорема единственности предела функции в точке
Теорема 1.
Если функция имеет предел в точке, то он единственный.
Доказательство (от противного).
Предположим, что  и
и  . Тогда, согласно определению предела,
. Тогда, согласно определению предела, 


 и
и 

 . Примем за
. Примем за  и
и  =
= 

 . Тогда
. Тогда  справедливы оба предположения. Возьмем
справедливы оба предположения. Возьмем  и оценим
и оценим 
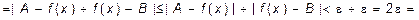
 , т. е.
, т. е.  – противоречие, следовательно, предположение не верно и предел единственный.
– противоречие, следовательно, предположение не верно и предел единственный.
условия существования предела функции в точке
Обозначим  – левая полуокрестность, т.е
– левая полуокрестность, т.е  .
.
Обозначим  – правая полуокрестность, т.е
– правая полуокрестность, т.е  .
.
Определение 3.
Число b называется левосторонним пределом функции 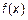 в точке
в точке  , если
, если 

 . Обозначается
. Обозначается  .
.
Определение 4.
Число b называется правосторонним пределом функции 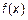 в точке
в точке  , если
, если 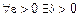

 . Обозначается
. Обозначается  . Левосторонние и правосторонние пределы называются односторонними.
. Левосторонние и правосторонние пределы называются односторонними.
Теорема 2.
Для того чтобы функция имела предел, необходимо и достаточно, чтобы существовали левосторонний и правосторонний пределы и были равны между собой.
Доказательство.
Необходимость.
Дано:  . Доказать, что
. Доказать, что 
 . По определению 2 следует, что
. По определению 2 следует, что 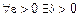
 следует
следует 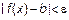 (2). Возьмем
(2). Возьмем  , согласно (2)
, согласно (2)  . Аналогично
. Аналогично  , согласно (2)
, согласно (2)  .
.
Достаточность.
Дано: 
 . Необходимо доказать, что
. Необходимо доказать, что  . По условию и определению 3
. По условию и определению 3 
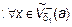
 . а по условию и определению 4
. а по условию и определению 4 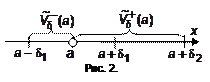
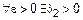

 . Примем за
. Примем за  . Тогда
. Тогда 

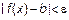 (рис. 2).
(рис. 2).
4. Свойства функции, имеющей предел в точке
Теорема 3.
Если функция имеет положительный предел в точке, то найдется окрестность точки, в которой функция положительна.
Доказательство.
Из определения следует, что 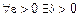
 , удовлетворяющих неравенству
, удовлетворяющих неравенству 
 . Следовательно,
. Следовательно,  или
или  . Возьмем
. Возьмем 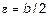 - любое положительное число. Тогда
- любое положительное число. Тогда  или
или  . Следовательно, все значения
. Следовательно, все значения 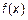 в
в  -окрестности точки a положительны (
-окрестности точки a положительны ( ). То же для отрицательного предела.
). То же для отрицательного предела.
Определение 5.
Функция 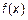 - ограниченная на множестве D если существует M>0, такое что
- ограниченная на множестве D если существует M>0, такое что  для любых
для любых  .
.
ПРИМЕР 3.
 - ограничена на R,
- ограничена на R,  ,
,  на области определения не ограничена, а на отрезке
на области определения не ограничена, а на отрезке  - ограничена
- ограничена 
Теорема 4.
Если функция имеет конечный предел в точке, то она ограничена в некоторой окрестности этой точки.
Доказательство.
Пусть  , тогда по определению
, тогда по определению 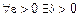
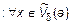
 . Очевидно, что
. Очевидно, что  . Следовательно,
. Следовательно,  или
или  . Обозначим
. Обозначим  , тогда
, тогда 
 , т. е. функция ограничена.
, т. е. функция ограничена.
Теорема 5.
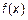 имеет конечный предел в точке, то
имеет конечный предел в точке, то  ограничена в некоторой окрестности этой точки.
ограничена в некоторой окрестности этой точки.
Доказательство аналогично теореме 4.
5. Предел функции на бесконечности
 Определение 6.
Определение 6.
N–окрестностью бесконечно удаленной точки называется множество всех точек рас, стояние до которых большее N или  , или
, или  . Обозначается
. Обозначается 
Определение 7.
Число b называется пределом функции 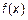 на бесконечности, если для
на бесконечности, если для 

 . Обозначается
. Обозначается
 . (3)
. (3)
Замечание!
Так как принципиального различия между определениями 7 и 1, 2 нет, то все рассмотренные теоремы можно отнести к функциям, имеющим предел на бесконечности.
Заключение
В заключении важно отметить, что предел – это абстрактное понятие, записанное строгим математическим языком, т. е. предел – это то значение, к которому стремится функция, причем она его может никогда не достичь (функция в этой точке может не существовать). Отметим, что предел функции в точке можно понимать как бесконечность вселенной и времени.
Отметим, что:
- предел – это абстракция, к которой что-то стремиться;
- функция ограничена в окрестностях, где она имеет предел;
- односторонние пределы могут быть не равными, т.е. может быть разрыв;
- доказательство всех теорем о пределах базируется на фундаментальном определении самого предела;
- функция может быть ограничена на бесконечности;
- всегда можно взять дельта-окрестность меньше той, которая дана.
Литература
1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980.
2. Фихтенгольц Г.М. «Основы математического анализа» Часть 1 – М.: Лань, 2002, - 448 с.
3. Натансон И.П. «Теория функций вещественной переменной». – СПб.: Лань, 1999, - 560 с.