Производная постоянной величины

Производная постоянной величины (рис. 1), т. е. функции , была рассмотрена в примере 1 (см. л. 6, ч. 2). Напомним, что приращение функции 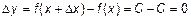, следовательно, 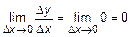, т. е. 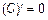. Другими словами, угол между прямой 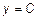и осью равен , т. е. прямая || .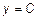

Следствие!

Производная произведения функции и константы равна произведению константы на производную функции, поскольку производная константы равна нулю .

1.2. Производная независимой переменной

1. Пусть 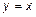– независимая переменная или прямая (рис. 2). Аргументу 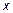дадим приращение .

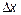2. Найдем соответствующее приращение функции .

3. Запишем очевидное отношение и найдем его предел , то есть (см. рис. 2).

Следствия!

1. 2. 3.

2. Производная степенной функции

Пусть , где , дифференцируема.

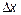1. Аргументу дадим приращение , функции – приращение , и новое значение .

2. Найдем соответствующее приращение функции = .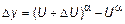

3. Найдем предел . Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента 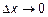соответствует бесконечно малое приращение функции , то есть получаем неопределенность 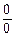. Тогда последний предел 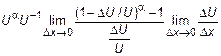= , откуда согласно пятому замечательному пределу имеем

. (1)

Производная степенной функции равна произведению показателя функции на функцию с показателем, уменьшенным на единицу, и на производную основания функции.

Следствия!

1. . 2. . 3. .

3. Производная показательной функции

Пусть , где 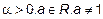, дифференцируема.

1. Аргументу 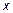дадим приращение 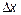, функции – приращение , и новое значение .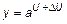

2. Найдем соответствующее приращение функции .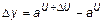

3. Запишем отношение и найдем его предел = 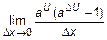. Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента 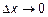соответствует бесконечно малое приращение функции . Тогда последний предел 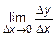= = = 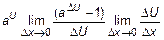, откуда согласно четвертому замечательному пределу имеем

. (2)

Производная показательной функции равна произведению самой функции на натуральный логарифм основания и на производную показателя.

Следствия!

1. 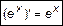. 2. .

4. Производная логарифмической функции

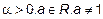Пусть , где , дифференцируема.

1. Аргументу 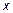дадим приращение 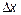, функции – приращение , и новое значение .

2. Найдем соответствующее приращение функции .

3. Найдем предел 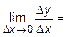= . Из необходимого условия дифференцируемости следует, что бесконечно малому приращению аргумента 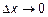соответствует бесконечно малое приращение функции . Тогда последний предел , откуда согласно третьему замечательному пределу имеем , или

. (3)

Производная логарифма функции равна произведению отношению производной функции к произведению функции на натуральный логарифм основания.

Следствия!

1. . 2. . 3. .

5. Производные тригонометрических функций

5.1. Производная sin x

Пусть , где дифференцируема.

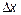1. Аргументу дадим приращение , функции – приращение , и новое значение .

2. Найдем соответствующее приращение функции .

3. Найдем предел 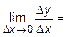= = 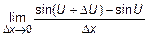= , или

. (4)

Производная синуса функции равна произведению косинуса функции на производную функции.

Следствие! .

5.2. Производная cos x

Пусть , где дифференцируема. Производная сложной функции . С другой стороны, . Откуда

. (5)

Производная косинуса функции равна произведению синуса функции на производную функции с противоположным знаком.

Следствие!

.

5.3. Производная tg x и ctg x

Пусть , где дифференцируема,

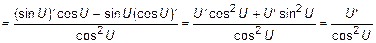
. (6)

Производная тангенса функции равна произведению квадрата секанса функции на производную функции.

Аналогично получим производную для котангенса.

. (7)

Производная котангенса функции равна произведению квадрата косеканса функции на производную функции с противоположным знаком.

Следствия!

1. . 2. .

5.4. Производная sec x и cosec x

Пусть , где дифференцируема, тогда

, или

. (8)

Производная секанса функции равна произведению секанса функции на тангенс функции и на производную функции. Аналогично

. (9)

Производная косеканса функции равна произведению косеканса функции на котангенс функции и на производную функции с противоположным знаком.

Следствия!

1. . 2. .

6. Производные обратных тригонометрических функций

6.1. Производная arcsin x и arccos x

Пусть , где , . Воспользуемся теоремой о производной обратной функции . Запишем . Тогда . Если дифференцируема, то

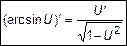. Аналогично . (10)

Следствия!

1. . 2. .

6.2. Производная arctg x и arcctg x

Пусть , где , . Запишем . Тогда .

Если дифференцируема, то

. Аналогично . (11)

Следствия!

1. . 2. .

7. Производные гиперболических функций

Производная sh x, ch x, th x, cth x

1. , .

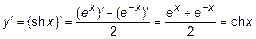2. , .

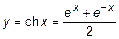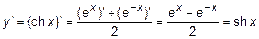3. , тогда .

4. 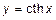, тогда .

Если дифференцируема, то окончательно запишем

, , , .

Заключение

Рассмотренные вопросы имеют больше практическое, чем теоретическое значение. Новые теории не изучались и не доказывались теоремы. Все производные получены на основе общего правила дифференцирования. Однако полученные результаты входят в основную часть таблицы производных, которую необходимо знать.

Отметим, что:

- производная константы равна нулю;

- производная аргумента равна единице;

- производная экспоненциальной функции равна самой функции.

Литература

1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997. – 190 с.

2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.

Лекция 9. Дифференциал функции

Цель лекции: изучить понятие дифференциала; понять его геометрический смысл; научиться применять дифференциал в приближенных вычислениях.

План лекции

1. Понятие дифференциала и его геометрический смысл

2. Дифференциал сложной функции

3. Дифференциалы высших порядков

4. Применение дифференциалов к приближенным вычислениям

5. Векторная функция скалярного аргумента и ее дифференциал

6. Дифференциал длины дуги

Введение

Ранее производные функций рассматривались как мгновенная скорость роста, то есть узнавали, во сколько раз быстрее растет функция по отношению к росту аргумента в точке. Дифференциал функции, хотя и имеет общие правила с производной в их нахождении, однако несет совершенно другой геометрический смысл, а именно: происходит не приращение функции, а приращение касательной. Это свойство используется в приближенных вычислениях, поскольку вычислить текущее значение функции прямой линии проще, чем исходной функции.

Отдельно рассматривается понятие векторной функции. В силу ограниченности объема курса это понятие дается в рамках одного вопроса. Однако его понимание и дифференциала векторной функции необходимо при изучении тем: «Векторный анализ», «Интегральное исчисление» и др. Подобные функции встречаются практически во всех прикладных задачах на траекторию движения. Отдельно отметим важность понятий дифференциала функции в теме «Дифференциальные уравнения».

1. Понятие дифференциала и его геометрический смысл

1.1. Дифференциал функции

ПРИМЕР 1.

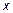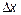Для при приращении на определить .

Решение.

Таким образом, состоит из двух частей (линейной и нелинейной) относительно .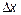

Пусть дифференцируема в некоторой точке 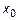, следовательно, существует или , следовательно, по второму определению предела 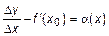– бесконечно малая величина в точке 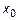. Выразим

, (1)

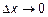при следует, что 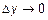. Сравним первое слагаемое с : . Следовательно ~ . Сравним второе слагаемое с : . Второе слагаемое (1) стремится к нулю быстрее, чем и даже 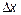. Обозначают .

Определение 1.

Главная, или линейная относительно 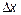, часть бесконечно малого приращения функции называется дифференциалом функции. Обозначается .

По определению . Для любых 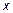дифференциал определяется как . Если , то = , или

. (2)

Согласно определению 1 и выражению (2) дифференциал функции определяется как

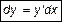, (3)

т. е. произведение производной этой функции на дифференциал независимой переменной. Из этого следует, что все формулы производных можно перенести на дифференциал.

1.2. Геометрический смысл дифференциала

Пусть – дифференцируемая функция. Обозначим через некоторую точку на кривой (рис. 1), приращение 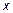– через 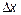, тогда вторую точку, образованную этим приращением на кривой, обозначим . В обозначим угол . Определим = 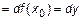, или .

Другими словами, дифференциал функции в точке, с геометрической точки зрения, есть приращение функции касательной в точке, тогда как приращение функции есть приращение ординаты точки графика. На рис. 1 видно, что . Очевидно, что для функции 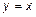приращение касательной равно приращению функции в точке , поскольку касательная у функции совпадает с самой функцией.

ПРИМЕР 2.

Найти для 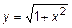. Имеем .

2. Дифференциал сложной функции

Если дифференцируема, 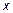– независимая переменная, тогда дифференциал . Если и – дифференцируемые функции, – независимая переменная, тогда – сложная функция, 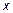– промежуточная переменная. Дифференциал . Сравнивая оба дифференциала простой и сложной функций, замечаем, что форма дифференциала не изменилась, то есть она не зависит от того, является ли аргумент независимой переменной или функцией. Это свойство называется инвариантностью дифференциала

. (4)

Однако в первом случае – число, а во втором случае – функция.

ПРИМЕР 3.

Дифференциалы , – инвариантны.

Производные , – не инвариантны.

3. Дифференциалы высших порядков

Определение 2.

Дифференциал от дифференциала первого порядка называется дифференциалом второго порядка 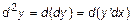. Поскольку – константа, то

. (5)

Определение 3.

Дифференциал от дифференциала второго порядка называется дифференциалом третьего порядка =

. (6)

Определение 4.

Дифференциал от дифференциала порядка называется дифференциалом n-го порядка = =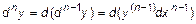

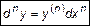. (7)

Определим дифференциал второго порядка сложной функции. Если дифференцируема, 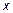– независимая переменная, тогда дифференциал второго порядка 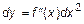. Если и – дифференцируемые функции, – независимая переменная, тогда – сложная функция, 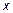– промежуточная переменная. Дифференциал второго порядка сложной функции . Однако – функция, поэтому . Сравнивая оба дифференциала простой и сложной функций, замечаем, что дифференциал второго, следовательно, и дифференциалы больших порядков не инвариантны.

4. Применение дифференциалов к приближенным вычислениям

Пусть – дифференцируема в точке 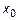, запишем + , где – более высокого порядка малости, чем 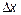. При приближенных вычислениях приращение функции можно заменить ее дифференциалом

, (8)

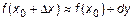т. е. , тогда , откуда

. (9)

Погрешность вычисления определяется выражением

, где . (10)

ПРИМЕР 4

Найти . Запишем соответствующую функцию , точку , приращение , значение функции в точке , производную и значение производной в точке . Тогда, используя выражение (9), определим .

Определим погрешность вычислений. . Данная функция убывает на отрезке 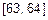, следовательно, 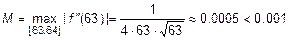. Тогда . С учетом погрешности .

5. Векторная функция скалярного аргумента и ее дифференциал

5.1. Векторная функция, ее непрерывность и производная

Запишем вектор . Если , то вектор – постоянный, если , и – функции, то

. (11)

Определение 5.

Отображение множества R на множество , которое каждому элементу из множества ставит в соответствие единственный элемент из множества , называется векторной функцией скалярного аргумента или вектор-функцией

.

Очевидно, что с изменением переменной t конец вектор-функции описывает некоторую линию в пространстве.

Определение 6.

Линия, описываемая концом векторной функции, называется годографом векторной функции. Начало векторной функции называется полюсом (рис. 2).

На векторную функцию переносятся все правила пределов, свойства непрерывности функции и правила дифференцирования.

Определение 7.

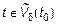Постоянный вектор называется пределом векторной функции в , если для любых существует , такая, что для любых следует 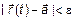, или по второму определению предела 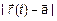есть бесконечно малая величина в точке .

Определение 8.

Векторная функция - непрерывна в точке , если она определена в этой точке и

Определение 9.

Производной векторной функции называется предел отношения приращения векторной функции к приращению аргумента, когда приращение аргумента стремиться к нулю

. (12)

5.2. Геометрический смысл производной векторной функции

Пусть векторной функции для приращения аргумента на 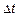соответствует приращение на (рис. 3). Очевидно, что вектор . При точка на кривой L

переходит в точку , т. е. или – касательный вектор. С геометрической точки зрения производная векторной функции есть вектор, касательный к годографу в данной точке.

Теорема 1.

. (13)

 

Доказательство.

1. Дадим параметру приращение 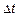, тогда функции также получать соответствующие приращения .

2. Запишем соответствующее приращение векторной функции .

3. Тогда предел , откуда .

Следствие!

(14)

5.3. Дифференциал длины дуги

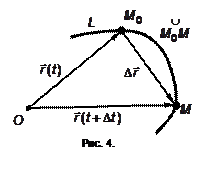Пусть L – годограф непрерывной векторной функции , причем непрерывно дифференцируема, а кривая L – гладкая. Определим длину дуги на кривой L (рис. 4). Очевидно, что длина дуги будет некоторой функцией .

Теорема 2.

(15)

Доказательство.

Дифференциал . Но . Очевидно, что при справедливо 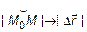, тогда , откуда справедливо (15).

5.5. Дифференциал длины дуги в различных видах

I. Кривая задана параметрически . По теореме Пифагора , или

. (16)

II. Функционально , где 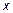– независимая переменная, тогда , или

. (17)

III. В полярной системе , , или

. (18)

Заключение

Отметим, что:

- дифференциал функции это приращение касательной в точке;

- дифференциал аргумента равен приращению аргумента;

- дифференциал используется в приближенных вычислениях;

- векторная функция это вектор с функциями координат;

- производная векторной функции это касательная к годографу векторной функции;

Литература

1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. – 384 с.

2. Фихтенгольц Г.М. «Основы математического анализа» Часть 1 – М.: Лань, 2002. - 448 с.

Лекция 10. Основные теоремы дифференцирования

Цель лекции: изучить основные теоремы дифференцирования; научиться использовать их для решения прикладных задач.

План лекции

1. Теорема Ферма

2. Теорема Ролля

3. Теорема Лагранжа

4. Теорема Коши

5. Теорема Лопиталя

6. Общая таблица взятия пределов

Введение

Ранее мы изучили понятия производной и дифференциала, и научились использовать их для решения прикладных задач. Однако решение многих задач можно упростить и найти решение некоторых неразрешенных задач на основе тех теорем, которые мы изучим сегодня. Они особенно важны для решения практических задач. Для усвоения теорем необходимы знания, полученные по темам «Дифференцирование» и «Пределы».

1. Теорема Ферма

1.1. Теорема ферма

Теорема 1 (Ферма).

Если функция непрерывна в окрестности точки 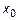, а в самой точке принимает наибольшее или наименьшее значение, то производная в этой точке равна нулю.

Доказательство.

Пусть – наибольшее значение функции 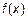, следовательно, для всех или . Тогда . Возможны два варианта.

а) Если 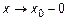, т. е. , и ,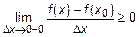

б) Если , т. е. , и .

По условию существует производная функции, тогда односторонние пределы равны между собой. Следовательно, 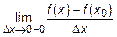= =0, или . Аналогично доказывается случай – наименьшее значение функции.

1.2. Геометрический смысл теоремы Ферма

Геометрический смысл теоремы состоит в том, что касательная в наибольшей и наименьшей точках графика функции (max или min) параллельна оси абсцисс (рис. 1).

Следствия!

1) Точка 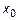– внутренняя. Если 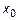– граничная точка, то теорема не выполняется.

2) Если не существует производной, то нет касательной.

3) Если производная , то касательная вертикальна.

2. Теорема Роля

Теорема 2 (Роля).

Если функция 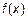непрерывна на отрезке и дифференцируема во всех внутренних точках этого отрезка, а на концах принимает равные значения , то хотя бы в одной точке внутри отрезка производная этой функции равна нулю

.

Доказательство.

Так как , то по теореме Вейерштрасса эта функция принимает на этом отрезке наибольшее и наименьшее значения. Возможны два случая.

1. Хотя бы одно наибольшее или наименьшее значение функция принимает внутри отрезка , например в точке 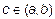, т. е