Отметим здесь, без доказательства, три важных свойства степенных рядов.
1.Сумма 
степенного ряда
| (2) |
является непрерывной функцией в каждой точке интервала сходимости 
.
2.Ряд
 ,
| (4) |
полученный почленным дифференцированием ряда (2), является степенным рядом с тем же, что и ряд (2), интервалом сходимости . Сумма ряда (4) 
.
Замечание. Ряд (4) также можно почленно дифференцировать и сумма полученного после этого ряда равна 
, и так далее. Таким образом, сумма ряда (2) является бесконечно дифференцируемой функцией в интервале сходимости . Сумма ряда полученного из ряда (2) 
– кратным дифференцированием, равна 
. Область сходимости степенного ряда при дифференцировании не изменится.
3. Пусть числа 
и 
принадлежат интервалу сходимости ряда (2). Тогда имеет место равенство
| (5) |
Формула трапеций Эта формула является более точной по сравнению с формулой прямоугольников Подынтегральная функция в этом случае заменяется на вписанную ломаную. Геометрически площадь криволи нейной трапеции заменяется суммой площадей вписанных трапеций.
Ряд Тейлора. Теорема о единственности разложения функции в ряд Тейлора
Ряд Тейлора. Пусть функция w = f (z) аналитична в области D, z 0∈ D. Обозначим L окружность с центром в z 0, принадлежащую области D вместе с ограниченным ею кругом. Тогда для любой точки z, лежащей внутри L, 
. Представим множитель 
в виде суммы сходящейся геометрической прогрессии: 
(так как | z – z 0| < | t – z 0|, то 
) 
, и ряд сходится абсолютно, поэтому его можно почленно интегрировать: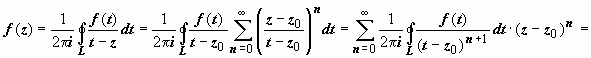 
, так как 
. Итак, 
.
Ряд в правой части этого равенства - ряд Тейлора функции f (z). Этот ряд абсолютно сходится внутри контура L, а в качестве L можно взять любую окружность, которая не выходит за пределы области D. Доказана
Теорема о разложении функции в ряд Тейлора. Если функция w = f (z) аналитична в области D, z 0 ∈ D, то функция f (z)может быть разложена в ряд Тейлора по степеням (z – z 0) n. Этот ряд абсолютно сходится к f (z) внутри круга | z – z 0| < r, где r - расстояние от z 0 до границы области D (до ближайшей к z 0 точке, в которой функция теряет аналитичность). Это разложение единственно.
Единственность разложения следует из того, что коэффициенты ряда однозначно выражаются через производные функции.
Необходимое и достаточное условие разложимости функции в ряд Тейлора
Рассмотрим задачу, обратную поставленной в разд. 30.4. Пусть функция 
бесконечно дифференцируема в т.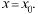 
Составим для
нее ряд Тейлора. Его сумма не всегда будет совпадать с функцией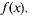 
Например, функция 
бесконечно дифференцируема при х = 0, причем 
поэтому для нее ряд
Маклорена 
Его сумма 
при х 
0. Выясним, при каких условиях 
О: Многочленом Тейлора степени п называется частичная сумма
Остаточным членом ряда Тейлора называется
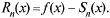(30.8)
Т: Для того чтобы бесконечно дифференцируемая в т.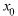 
функция 
являлась суммой составленного для нее ряда Тейлора (30.6), необходимо и достаточно, чтобы 
Используя определение сходящегося ряда и выражение (30.8), имеем следующую цепочку: 
— сумма (30.6) 
Приведем запись остаточного члена в форме Лагранжа [4. С. 168]:
(30.9) где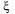 
находится между 
и х.