Решение типовых примеров

Номер варианта	А	В	С
1.
2.
3.
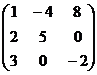
4.
5.
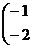
6.
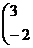
7.
8.
9.
10.
11.
12.
13.
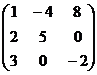
14.
15.
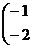
16.
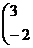
17.
18.
19.
20.
21.
22.
23.
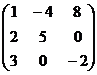
24.
25.
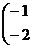
26.
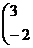
27.
28.
29.
30.

2. Вычислить определитель третьего порядка:

А) методом разложения по элементам строки или столбца,

Б) по правилу треугольника

1.	2.	3.	4.
5.	6.	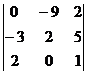7.	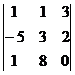8.
9.	10. .	11.	12.		4.
13.	14.	15.	16.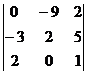

17. 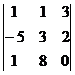1 8. 1 9. 2 0. .

21.	22.	23.	24.
25.	26.	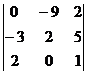27.	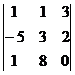28.
29.	30. .				4.

Решить систему линейных уравнений методами: а) обратной матрицы, б) Крамера, в) Гаусса.

1. , 2. , 3. ,

4. , 5. , 6.

7. , 8. , 9. ,

10. . 11. , 1 2. ,

13. , 14. , 15.

16. 1 7. , 1 8. ,

19. , 2 0. . 2 1. ,

2 2. , 2 3. , 24. ,

25. , 26. ,27. .

28. , 29. ,30

4. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр.

1. А (–5; 0), В (7; 9), С (5; –5).

2. А (–7; 2), В (5; 11), С (3; –3).

3. А (–5; –3), В (7; 6), С (5; –8).

4. А (–6; –2), В (6; 7), С (4; –7).

5. А (–8; –4), В (4; 5), С (2; –9).

6. А (0; –1), В (12; 8), С (10; –6).

7. А (–6; 1), В (6; 10), С (4; –4).

8. А (–2; –4), В (10; 5), С (8; –9).

9. А (–3; 0), В (9; 9), С (7; –5).

10. А (–9; –2), В (3; 7), С (1; –7).

11. А (–5; 2), В (7; –7), С (5; 7).

12. А (–7; 5), В (5; –4), С (3; 10).

13. А (–7; 1), (5; –8), С (3; 6).

14. А (0; 3), В (12; –6), С (10; 8).

15. А (–8; 4), В (4; –5), С (2; 9).

16. А (–2; 2), В (10; –7), С (8; 7).

17. А (1; 2), В (13; –7), С (11; 7).

18. А (–4; 1), В (8; –8), С (6; 6).

19. А (–7; –1), В (5; –10), С (3; 4).

20. А (–3; 3), В (9; –6), С (7; 8).

21. А (–5; 0), В (7; 9), С (5; –5).

22. А (–7; 2), В (5; 11), С (3; –3).

23. А (–5; –3), В (7; 6), С (5; –8).

24. А (–6; –2), В (6; 7), С (4; –7).

25. А (–8; –4), В (4; 5), С (2; –9).

26. А (0; –1), В (12; 8), С (10; –6).

27. А (–6; 1), В (6; 10), С (4; –4).

28. А (–2; –4), В (10; 5), С (8; –9).

29. А (–3; 0), В (9; 9), С (7; –5).

30. А (–9; –2), В (3; 7), С (1; –7).

5.Составить уравнение плоскости, проходящей через три данные точки и выполнить ее схематичный чертеж. Подставьте вместо n номер своего варианта.

А(3; 5; 4), B(4; n-10; 5), C(6; -2; 1).

Задача 6. Найдите площадь фигуры, разделив ее на треугольники. Используйте координаты точек из задания 4, добавив точки Д (4; 1) и К (-5; -3).

Решение типовых примеров

1. Сложить две матрицы и

Решение. Складывать (вычитать) можно только матрицы одинакового размера, а т.к. размеры матрицы А – (3´2) и В – (3´2) (где 3 – число строк, 2 – число столбцов) совпадают, то для того, чтобы сложить две матрицы, надо к каждому элементу первой матрицы прибавить соответствующие элементы второй матрицы:

+ = = .

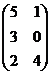Ответ: .

2. Умножить матрицу на число 3.

Решение. Для того, чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число:

.

Ответ: .

3. Умножить матрицу на матрицу .

Решение. Умножение матриц А и В определено, если число столбцов первой матрицы равно числу строк второй.

Совпадают

Размерность результирующей

матрицы

В нашем случае размер А – (2´3), а размер В – (3´3), поэтому умножение производить можно; размерность результирующей матрицы С – (2´3). Для того чтобы получить элемент, стоящий на пересечении i –й строки и j –го столбца новой матрицы, нужно элементы i –й строки первой матрицы умножить на соответствующие элементы j –го столбца второй матрицы и результат сложить, т.е. элементы матрицы С вычисляются по формуле:

.

C = ∙ =

= .

Ответ: C = .

4. Вычислить определитель 3-го порядка: .

Решение. 1) Метод разложения по элементам строки или столбца.

С помощью метода разложения по элементам строки (столбца) можно вычислить определители любого порядка. Строку (столбец), по элементам которого производится разложение, следует выбирать так, чтобы в ней содержалось наибольшее количество нулей.

Разложим определитель по элементам какой-либо строки или столбца. Например, выберем для разложения третий столбец:

= (1)

Здесь , , 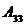– алгебраические дополнения элементов матрицы , , соответственно, которые в общем случае для элемента находятся по формуле

. (2)

Минор 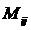– определитель, получаемый из исходного вычеркиванием i –й строки и j –го столбца, на пересечении которых стоит данный элемент. Например, для нахождения вычеркивается 1-я строка и 3-йстолбец:

.

Аналогично определяем , вычеркивая 2-ю строку и 3-й столбец.

получается вычеркиванием 3-й строки и 3-го столбца:

.

Тогда алгебраические дополнения (по формуле (2)) будут равны:

,

Подставляя найденные значения в (1), найдем определитель

.

Ответ: 27.

2) Метод Саррюса.

С помощью метода Саррюса можно вычислять только определители третьего порядка.

Сначала к исходному определителю справа приписываем первый и второй столбцы:

Тогда определитель равен сумме произведений элементов, стоящих на главной диагонали и диагоналях, параллельных ей, взятых со своими знаками, и произведению элементов побочной диагонали и параллельных ей диагоналях, взятых с противоположными знаками.

= 2∙4∙3 + 1∙0∙1 + 3∙5∙2 – 3∙4∙1 – 2∙0∙2 – 1∙5∙3 = 27.

^{– – – + + +}

Ответ: 27.

5. Найти матрицу, обратную матрице А = , и сделать проверку.

Решение. а) сначала вычислим определитель исходной матрицы

.

Так как определитель матрицы А не равен 0, то для нее существует обратная матрица А^-1.

b) Найдем транспонированную матрицу А^Т, которая получается из исходной заменой элементов строк элементами столбцов с сохранением порядка:

А^Т = .

с) Найдем алгебраические дополнения всех элементов транспонированной матрицы и составим из них матрицу А̃, которая называется присоединенной (или взаимной):

, , ,

А^Т₂₁ = (-1)²⁺¹ 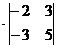= 1, А^Т₂₂ = (-1)²⁺² = 2, А^Т₂₃ = (-1)²⁺³ 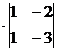= 1,

А^Т₃₁ =(-1)³⁺¹ 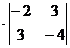= –1, А^Т₃₂ = (-1)³⁺² = 10, А^Т₃₃ = (-1)³⁺³ = 7.

А ̃ = .

d) Найдем обратную матрицу по формуле :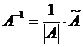

.

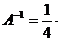
е) Проверим правильность нахождения обратной матрицы А ^-1: при умножении А ^-1 на исходную матрицу, должна получиться единичная матрица Е: А^-1∙А = Е.

А^-1∙А = ∙ = = Е.

Ответ: .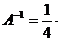

6. Решить систему линейных уравнений:

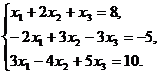
Решение. 1) Метод обратной матрицы.

Запишем систему в матричном виде. Для этого обозначим матрицу системы А= (она состоит из коэффициентов при переменных); столбец неизвестных Х = , столбец свободных членов В = , состоящий из правых частей уравнений. Тогда система представима в матричном виде: АХ=В.

Для нахождения Х необходимо умножить матричное уравнение на А^-1 слева: Х = А ^-1 ∙В.

Матрицу А ^-1 найдем по алгоритму, приведенному в примере 5. Получим:

.

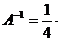
Тогда столбец неизвестных:

= = = .

2) Метод Крамера.

Выпишем определитель матрицы системы А:

Δ = = 4.

(Так как определитель не равен 0, то метод Крамера использовать можно, и система имеет единственное решение.)

Определитель Δ₁ получаем из определителя Δ заменой первого столбца на столбец свободных членов В, а остальные столбцы остаются прежними:

Δ₁ = = 4.

Аналогично, заменяя в исходном определителе второй, а затем третий столбцы на столбец свободных членов, получим соответственно Δ₂ и Δ₃.

Δ₂ = = 8, Δ₃ = =12.

Теперь воспользуемся формулой Крамера и найдем все переменные:

, , .

3) Метод Гаусса.

Метод Гаусса – это универсальный метод решения систем линейных уравнений. Он заключается в последовательном исключении переменных.

Составим расширенную матрицу системы, которая включает в себя матрицу системы и столбец свободных членов.

.

Произведем элементарные преобразования со строками матрицы, приведя ее к треугольному виду, т.е. к матрице, в которой все элементы, ниже главной диагонали равны нулю (при этом диагональные элементы не равны нулю).

Шаг 1. Если в матрице элемент а ₁₁ = 0, то перестановкой строк нужно добиться того, чтобы элемент а ₁₁≠ 0. В нашем примере а ₁₁≠ 0.

Сначала обнулим элементы первого столбца ниже главной диагонали. Для этого поочередно умножим элементы первой строки на числа = 2 и = –3 и прибавим соответственно к элементам второй и третьей строк:

_{2∙ -3}

+ + →

Шаг 2. Если в полученной матрице а ₂₂ ≠ 0, то обнулим элемент второго столбца ниже главной диагонали. Для этого умножим вторую строку на число и прибавим к третьей строке:

→ .

Полученная матрица имеет треугольный вид.

Т.о. получили систему уравнений:

Откуда найдем из последнего уравнения х ₃ = 3; из второго х ₂ = =2; из первого х ₁ = 8 – 2 х ₂ – х ₃ = 1.

Ответ: х ₁ = 1, х ₂ = 2, х ₃ = 3.

Задача 4. Даны вершины треугольника АВС: А (–4; 8), В (5; –4), С (10; 6).

Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр.

Решение. 1. Расстояние между точками и определяется по формуле:

. (1)

Подставив в эту формулу координаты точек А и В, имеем:

.

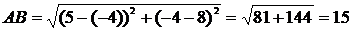2. Уравнение прямой, проходящей через точки и , имеет вид:

. (2)

Подставив в (2) координаты точек:

Для нахождение углового коэффициента прямой АВ разрешим полученное уравнение относительно у: . Отсюда . Подставив в формулу (2) координаты точек А и С, получим уравнение прямой АС.

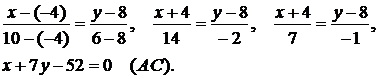
Отсюда .

3. Угол между двумя прямыми, угловые коэффициенты которых равны и , определяется по формуле:

. (3)

Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее , .

,

рад.

4. Так как высота перпендикулярна стороне , то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

.

Уравнение прямой, проходящей через данную точку в заданном угловым коэффициентом направлении, имеет вид:

. (4)

Подставив в (4) координаты точки С и , получим уравнение высоты :

. (5)

Для нахождения длины определим координаты точки , решив систему уравнений (АВ) и ():

откуда , то есть .

Подставив в формулу (1) координаты точек С и , находим:

.

5. Уравнение окружности радиуса с центром в точке имеет вид:

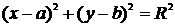. (6)

Так как является диметром искомой окружности, то ее центр Е есть середина отрезка . Воспользовавшись формулами деления отрезка пополам, получим:

Следовательно, 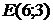и . Используя формулу (6), получаем уравнение искомой окружности:

.

На рис. 1 в декартовой прямоугольной системе координат изображен треугольник , высота , окружность с центром в точке Е.