Задания для контрольных работ

ИВАНОВСКИЙ ФИЛИАЛ

Кафедра Математики, экономической информатики и вычислительной техники

МАТЕМАТИКА

Методические указания по выполнению

Контрольных работ

Для студентов 2 курса заочного отделения

Всех факультетов

Иваново, 2004

Составитель: старший преподаватель Груздева Н.Н.

 

Редактор:

 

Математика. Контрольные задания для студентов первого курса заочного отделения всех факультетов (экономические специальности) и методические рекомендации по их выполнению.

Рецензент: М.А. Ноздрин (кандидат технических наук, доцент Ивановского государственного университета)

 

 

Математика.

Методические указания по выполнению

контрольных работ

для студентов 2 курса заочного отделения

всех факультетов

 

Составитель: Груздева Надежда Николаевна

 

Редактор:

 

Лицензия

 

 

Подписано в печать _______________ Формат 60 х 84 1/16

Печать плоская Усл. Печатных листов ______ Тираж 200 экз.

Заказ ____________________

 

Ивановский государственный энергетический университет

 

Типография ИЭУ, г. Иваново, ул. Ермака, 41

Общие рекомендации студенту-заочнику по работе над курсом

Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом. По курсу Математики она складывается из чтения учебной литературы и решения задач при выполнении контрольных заданий. В помощь студентам заочного отделения университет организует чтение лекций, практические занятия и консультации. Указания студенту по текущей работе даются также в процессе рецензирования контрольных работ. Однако студент должен помнить, что только при систематической и упорной самостоятельной работе помощь университета будет достаточно эффективной.

Завершающим этапом изучения курса в конце семестра является сдача экзамена в соответствии с учебным планом.

 

Рекомендации по выполнению контрольной работы

* В процессе изучения курса Математики студент второго курса заочного отделения должен выполнить две контрольные работы. Рецензии на эти работы позволят студенту судить о степени усвоения им соответствующего раздела курса. Также в них преподаватель указывает на имеющиеся пробелы, на желательное направление дальнейшей работы.

* Не следует приступать к выполнению задания контрольной работы до решения достаточного количества задач по учебному материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить то или иное задание контрольной работы вызвано тем, что студент не выполнил это требование.

* Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа не дает возможности преподавателю-рецензенту указать студенту на недостатки в его работе, в усвоении им учебного материала. В результате чего студент не приобретает необходимых знаний и может оказаться не подготовленным к экзамену.

* Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления контрольной работы и рецензии на нее студент не допускается до сдачи экзамена.

 

Рекомендуемая литература

1. Гмурман В.Е. Теория вероятностей и математическая статистика, М.: Высшая школа, 1977.

2. Данко И.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, Части 1, 2, М.: Высшая школа, 1980

3. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. Часть 1, 2. М.: Высшая школа, 1982.

4. Кремер Н.Ш. Высшая математика для экономистов: Учебник для вузов, М.: Банки и биржи, ЮНИТИ, 1999.

5. Маркович Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики, М.: Высшая школа, 1972.

6. Минорский В.П. Сборник задач по высшей математике, М.: Наука, 1986.

Рекомендации по самостоятельной работе

 

Примеры решения контрольных заданий

Задание 1. Предприятие выпускает два вида продукции А и В, для производства которых используется сырье трех видов. На изготовление единицы изделия А требуется затратить сырья каждого вида 2, 3, 5 кг соответственно, а для единицы изделия В – 7, 3, 1 кг. Производство обеспечено сырьем каждого вида в количестве 560, 300, 332 кг соответственно. Стоимость единицы изделия А составляет 55 руб., а единицы изделия В – 35 руб. Требуется составить план производства изделия А и В, обеспечивающий максимальную стоимость готовой продукции.

Выполнить следующие задания:

а) Составить математическую модель задачи:

б) Решить задачу геометрически;

в) Решить задачу симплекс-методом;

г) Сформулировать двойственную задачу и найти ее решение.

 

Решение.

а) Составим математическую модель задачи. Пусть X₁ - количество изделий вида А в требуемом плане производства, а X₂ - количество изделий вида В в требуемом плане производства, X₁ ≥ 0, X₂ ≥ 0.

 

Для данного плана производства потребуется:

· сырья 1-го типа для изделий вида А - 2X₁ кг, для изделий вида В - 7X₂ кг, по условию задачи: 2X₁ + 7X₂ ≤ 560;

· сырья 2-го типа для изделий вида А - 3X₁ кг, для изделий вида В - 3X₂, по условию задачи: 3X₁ + 3X₂ ≤ 300.

· сырья 3-го типа для изделий вида А - 5X₁ кг, для изделий вида В - X₂ кг, по условию задачи: 5X₁ + X₂ ≤ 332.

 

При реализации будет получена прибыль:

F = 55X₁ + 35X₂ руб.

Таким образом, получили математическую модель задачи.

 

Найти такие значения переменных X₁ и X₂, которые будут удовлетворять системе ограничений (1) и обращают в максимум целевую функцию (2):

 

2X₁ + 7X₂ ≤ 560

3X₁ + 3X₂ ≤ 300 (1)

5X₁ + X₂ ≤ 332

X₁ ≥ 0, X₂ ≥ 0 F = 55X₁ + 35X₂ → max (2)

 

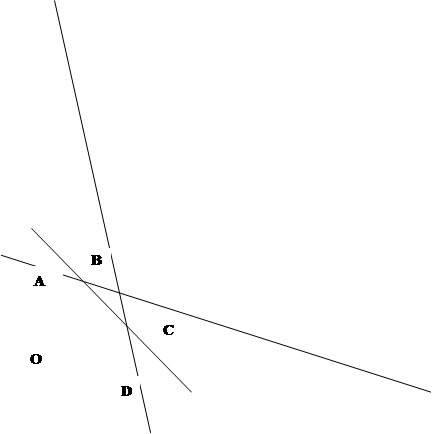
б) Решим данную задачу геометрическим методом. Построим граничные прямые l₁, l₂, l₃ для первого, второго и третьего неравенства соответственно и выберем ту полуплоскость, которая будет являться решением.

 

X1
X2

l₁: 2X₁ + 7X₂ = 560|: 2

X₁ + 3,5X₂ = 280

 

 

X1
X2

l₂: 3X₁ + 3X₂ =300|: 3

X₁ + X₂ = 100

 

 

X1		66,4
X2

l₃: 5X₁ + X₂ = 332|: 5

X₁ + 0,2X₂ = 66,4

 

 

X2
50
								X1
			l2					l1
		l3

 

Область решений – многоугольник ОАВСD.

Оптимальное решение находится, по крайней мере, в одной из вершин многоугольника . Найдем их координаты:

А (0; 80) F_A = 55·0 + 35·80 = 2800

D (66,4; 0) F_D = 55·66,4 + 35·0 = 3652

В = L ₁ ∩ L ₂

X₁ + 3,5X₂ = 280

X₁ + X₂ = 100

2X₂ = 180

X₂ = 72

X₁ = 100 – 72 = 28

F_B = 55·28 + 35·72 = 4090

С = L ₂ ∩ L ₃

X₁ + X₂ = 100

X₁ + 0,2X₂ = 66,4

0,8X₂ = 33,6

X₂ = 42

X₁ = 100 – 42 = 58

F_C = 55·58 + 35·42 = 4660

Т.к. значение целевой функции больше в точке С, то ее координаты и будут ответом задачи.

Ответ: при оптимальном плане выпуска продукции необходимо выпускать изделия вида А в количестве 58 единиц, изделия вида В – 42 единицы, при этом максимальная прибыль составит 4660 рублей.

 

в) Решим задачу симплекс-методом:

2X₁ + 7X₂ ≤ 560

3X₁ + 3X₂ ≤ 300

5X₁ + X₂ ≤ 332

X₁ ≥ 0, X₂ ≥ 0 F = 55X₁ + 35X₂ → max.

 

Приведем задачу к каноническому виду. Пусть X₃ кг, X₄ кг, X₅ кг – это остатки сырья каждого типа соответственно после производства продукции, тогда получим:

2X₁ + 7X₂ + X₃ = 560,

3X₁ + 3X₂ + X₄ = 300,

5X₁ + X₂ + X₅ = 332;

X₁ ≥ 0, X₂ ≥ 0, X₃ ≥ 0, X₄ ≥ 0, X₅ ≥ 0.

Запишем первую симплексную таблицу:

 

Основные переменные	X1	X2	X3	X4	X5	Свободные члены	Оценка
X3
X4
X5							66,4
-F							max

 

Данный план не оптимальный, так как в индексной строке есть положительные числа. Максимальное положительное число в индексной строке «55» определяет, что первый столбец ключевой. В последнем столбце таблицы вычислим оценку роста каждой базисной переменной как частное от деления свободного члена на соответствующий коэффициент ключевого столбца. Минимальная оценка «66,4» определяет, что третья строка – ключевая. Таким образом, разрешающий элемент – 5, α * = 5.

Запишем вторую симплексную таблицу:

Сначала выведем из базиса переменную X₅ из ключевой строки, а ее место займет переменная из ключевого столбца – это Х₁. Столбцы, соответствующие базисным переменным заполним следующим образом: напротив «своей» переменной ставим 1, а в остальные клетки столбца ставим 0. Заполнили строку, которая соответствует ключевой строке из прошлой таблицы, разделив ее элементы на разрешающий элемент:

α ₃₂ = 1/5 = 0,2; α ₃₅ = 1/5 = 0,2; в ₃ = 332/5 = 66,4.

 

Остальные клетки таблицы заполнили по правилу прямоугольника:

α ₁₂ = (7·5-2·1)/5 = 6,6; α ₁₅ = (0·5-2)/5 = -0,4; в ₁ = (560·5-2·332)/5 = 427,2;

α ₂₂ = (3·5-3)/5 = 2,4; α ₂₅ = (0·5-3)/5 = -0,6; в ₂ = (300·5-332·3)/5 = 100,8;

с ₂ = (35·5-55)/5 = 24; с ₅ = (0-55)/5 = -11; -F = (0-332·55)/5 = -3652.

 

Основные Переменные	X1	X2	X3	X4	X5	Свободные члены	Оценка
X3		6,6			-0,4	427,2	≈ 65
X4		2,4			-0,6	100,8
X1		0,2			0,2	66,4
-F					-11	-3652	max

 

 

Данный план не оптимальный, т.к. в индексной строке остался положительный элемент - число «24». Повторим пересчет симплексной таблицы.

α * = 2,4.

 

Запишем третью симплексную таблицу:

Сначала выведем из базиса переменную X₄ из ключевой строки, а ее место займет переменная из ключевого столбца – это Х₂. Столбцы, соответствующие базисным переменным заполним следующим образом: напротив «своей» переменной ставим 1, а в остальные клетки столбца ставим 0. Заполнили строку, которая соответствует ключевой строке из прошлой таблицы, разделив ее элементы на разрешающий элемент:

α ₂₄ = 1/2,4 = 5/12; α ₂₅ = -0,6/2,4 = -0,25; в ₂ = 100,8/2,4 = 42.

Остальные клетки таблицы заполнили по правилу прямоугольника:

α ₁₄ = -6,6/2,4 = -2,75; α ₁₅ = (-0,4·2,4-(-0,6)·6,6)/2,4 = 1,25; в ₁ =(427,2·2,4-6,6·100,8)/2,4 =150;

α ₃₄ = (-0,2)/2,4 = -1/12; α ₃₅ = (0,2·2,4-0,2·(-0,6))/2,4 = 0,25; в ₃ = (66,4·2,4-0,2·100,8)/2,4 = 58;

с ₄ = (-24)/2,4 = -10; с ₅ = (-11·2,4-(-0,6)·0,2)/2,4 = -5; -F = (-3652·2,4-100,8·24)/2,4 = -4660.

 

Основные переменные	X1	X2	X3	X4	X5	Свободные члены	Оценка
X3				-2,75	1,25
X2				5/12	-0,25
X1				-1/12	0,25
-F				-10	-5	-4660	max

 

В индексной строке нет положительных чисел, значит, критерий оптимальности выполнен, и данный план является оптимальным.

 

Ответ: при оптимальном плане выпуска продукции необходимо выпустить изделия вида А в количестве 58 единиц, изделия вида В – 42 единицы, при этом получим следующие остатки сырья: 1-го типа – 150 кг, а 2-го и 3-го типа сырья не останется, максимальная прибыль составит 4660 рублей.

 

г) Составим двойственную задачу и найдем ее решение:

Составим задачу 2 – двойственную к исходной задаче 1, используя свойства двойственных задач:

а). в одной задаче ищут максимум линейной функции, а в другой – минимум;

б). коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений другой;

в). каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида «£», а в задаче минимизации – все неравенства вида «³».

г). матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.

Задача 1 (Исходная)	Задача 2 (Двойственная)
2X1 + 7X2 ≤ 560 3X1 + 3X2 ≤ 300 5X1 + X2 ≤ 332 X1 ≥ 0, X2 ≥ 0 F = 55X1 + 35X2 → max	2 у 1 + 3у2 + 5 у 3 ≥ 55 7 у 1 + 3 у 2 + у 3 ≥ 35 у 1 ≥ 0, у 2 ≥ 0, у 3 ≥ 0   Z = 560 у 1 + 300 у 2 + 332 у 3 → min

 

Так как первоначальным переменным исходной задачи соответствуют дополнительные переменные двойственной задачи и наоборот, то согласно последней симплексной таблице имеем:

у ₁ =0, у ₂ = 10, у ₃ = 5, у ₄ = 0, у ₅ = 0,

Таким образом:

Z min= 560·0 + 300·10 + 332·5 = 4660, что соответствует оптимальному значению целевой функции исходной задачи: F max = Z min.

 

Задание 2. На трех базах А₁, А₂, А₃ (ПО - пункты отправления) находится однородный груз в количестве а₁, а₂, а₃ т. Этот груз необходимо развести пяти потребителям В₁, В₂, В₃, В₄, В₅ (ПН - пункты назначения), потребности которых в этом грузе составляют в₁, в₂, в₃, в₄, в₅ т соответственно. Стоимость перевозок пропорциональна расстоянию и количеству перевозимого груза. Матрица тарифов и значения а₁, а₂, а₃ и в₁, в₂, в₃, в₄, в₅ приведены в таблице. Требуется спланировать перевозки так, чтобы их стоимость была минимальной.

 

ПН ПО	В1	В2	В3	В4	В5	Запасы (aj)
А1
А2
А3
Заявки (в j)

 

Решение.

Получим первый план перевозок методом «наименьшего тарифа», в котором приоритетом на перевозку обладает та клетка, в которой тариф на перевозку наименьший.

ПН ПО	В1	В2	В3	В4	В5	Запасы (aj)
А1	200 3	-10	-6	-13	-8
А2	- 7	100 5	-11	-16	200 4
А3	20 12	20 15	160 18	100 9	-10
Заявки (в j)

Для первой транспортной таблицы найдем затраты на перевозку:

F = 200·3 + 100·5 + 200·4 + 20·12 + 20·15 + 160·18 + 100·9 = 600 + 500 + 800 + 240 + 300 + 2880 + 900 = 6220 (руб.)

Проверим критерий оптимальности по методу потенциалов, в котором для каждой заполненной клетки составим уравнение a_i + b_j = c_ij, где a_i – потенциал строки, b_j – потенциал столбца, c_ij – истинный тариф клетки. Для полученного первого плана перевозок имеем:

a₁ + b₁ = 3

a₂ + b₂ = 5

a₂ + b₅ = 4

a₃ + b₁ = 12

a₃ + b₂ = 15

a₃ + b₃ = 18

a₃ + b₄ = 9

 

Так как число уравнений на одно меньше, чем число неизвестных, то одна переменная должна быть свободная, пусть это будет a₁, и она равна 0. В соответствии с этим найдем значения всех остальных неизвестных:

a₁ = 0 b₁ = 3 b₄ = 0

a₂ = -1 b₂ = 6 b₅ = 5

a₃ = 9 b₃ = 9

Для свободных (незаполненных) клеток найдем косвенные тарифы, как сумму потенциалов соответствующей строки и столбца, и сравним их с истинными тарифами:

С¢₁₂ = a₁ + b₂ = 0 + 6 = 6 < 10

С¢₁₃ = a₁ + b3 = 0 + 9 = 9 < 6

С¢₁₄ = a₁ + b₄ = 0 + 0 = 0 < 13

С¢₁₅ = a₁ + b₅ = 0 + 5 = 5 < 8

С¢₂₁ = a₂ + b₁ = -1 + 3 = 2 < 7

С¢₂₃ = a₂ + b₃ = -1 + 9 = 8 < 11

С¢₂₄ = a₂ + b₄ = -1 + 0 = -1 < 16

С¢₃₅ = a₃ + b₅ = 9 + 5 = 14 > 10

Так как в клетке (3;5) косвенный тариф больше истинного, то критерий оптимальности не выполнен, значит, данное распределение перевозок не оптимально и требует пересчета.

 

Для клетки (3;5) построим цикл пересчета:

 

100 (2;2) + - (2;5) 200

 

20 (3;2) - + (3;5)

Отметим знаком "+" вершину цикла с адресом (3; 5), а в остальных вершинах чередуем знаки. Найдем величину переводимой поставки ∆ как минимум значений в отрицательных вершинах цикла: ∆ = min{200; 20} = 20.

Значение ∆ прибавим к значениям в положительных вершинах цикла и вычтем из значений в отрицательных вершинах. Таким образом, поставка в (2;2) - 120, в (2;5) - 180, в (3;5) - 20, в (3;5) нет поставки.

Построим новую транспортную таблицу:

 

ПН   ПО	В1	В2	В3	В4	В5	Запасы (aj)
А1	200 3	-10	-6	-13	-8
А2	- 7	120 5	-11	-16	180 4
А3	20 12	- 15	160 18	100 9
Заявки (в j)

 

Проверим критерий оптимальности для этой таблицы:

a₁ + b₁ = 3

a₂ + b₂ = 5

a₂ + b₅ = 4

a₃ + b₁ = 12

a₃ + b₅ = 10

a₃ + b₃ = 18

a₃ + b₄ = 9

a₁ = 0 b₁ = 3 b₄ = 0

a₂ = 3 b₂ = 2 b₅ = 1

a₃ = 9 b₃ = 9

Найдем косвенные тарифы для всех незаполненных клеток:

С¢₁₂ = a₁ + b₂ = 0 + 2 = 2 < 10

С¢₁₃ = a₁ + b₃ = 0 + 9 = 9 > 6

С¢₁₄ = a₁ + b₄ = 0 + 0 = 0 < 13

С¢₁₅ = a₁ + b₅ = 0 + 1 = 1 < 8

С¢₂₁ = a₂ + b₁ = 3 + 3 = 6 < 7

С¢₂₃ = a₂ + b₃ = 3 + 9 = 12 > 11

С¢₂₄ = a₂ + b₄ = 3 + 0 = 3 < 16

С¢₃₂ = a₃ + b₂ = 9 + 2 = 11 < 15

Критерий оптимальности не выполнен, потому что в клетках (1;3) и (2;3) косвенные тарифы больше истинных, и так как в клетке (1;3) разница между косвенным и истинным тарифом больше, то цикл пересчета построим именно для нее:

200 (1;1) - + (1;3)

 

20 (3;1) + - (3;5) 160

∆ = min{200; 160} = 160, таким образом, имеем поставки: в (1;1) - 40, в (1;3) - 160, в (3;1) - 180, в (3;5) нет поставки.

Построим новую транспортную таблицу:

 

ПН   ПО	В1	В2	В3	В4	В5	Запасы (aj)
А1	40 3	-10		-13	-8
А2	-7	120 5	-11	-16	180 4
А3	180 12	- 15	- 18	100 9	20 10
Заявки (в j)

 

Проверим критерий оптимальности для этой таблицы:

 

a₁ + b₁ = 3

a₁ + b₃ = 6

a₂ + b₂ = 5

a₂ + b₅ = 4

a₃ + b₁ = 12

a₃ + b₄ = 9

a₃ + b₅ = 10

 

a₁ = 0 b₁ = 3 b₄ = 0

a₂ = 3 b₂ = 2 b₅ = 1

a₃ = 9 b₃ = 6

Найдем косвенные тарифы для всех незаполненных клеток:

С¢₁₂ = a₁ + b₂ = 0 + 2 = 2 < 10

С¢₁₄ = a₁ + b₄ = 0 + 0 = 0 < 13

С¢₁₅ = a₁ + b₅ = 0 + 1 = 1 < 8

С¢₂₁ = a₂ + b₁ = 3 + 3 = 6 < 7

С¢₂₃ = a₂ + b₃ = 3 + 6 = 9 < 11

С¢₂₄ = a₂ + b₄ = 3 + 0 = 3 < 16

С¢₃₂ = a₃ + b₂ = 9 + 2 = 11 < 15

С¢₃₃ = a₃ + b₃ = 9 + 6 = 15 < 18

Т.к. для всех незаполненных клеток косвенные тарифы меньше истинных, то данный план оптимальный, и он – единственный. Найдем затраты на перевозку по оптимальному плану:

F min = 40·3 + 160·6 + 120·5 + 180·4 + 180·12 + 100·9 + 20·10 = 120 + 960 + 600 + 720 + 2160 + 900 + 200 = 5660 (рублей)

Экономия от оптимизации опорного плана составила:

∆ F = F - F min = 6220 - 5660 = 560 (рублей)

 

Задание 3. Решить игру с «природой» с платежной матрицей А, если:

а) известны вероятности чистых стратегий «природы» 0,3; 0,2; 0,1; 0,4

б) поведение «природы» не определено. Найти оптимальные стратегии игрока по критериям Вальда, Сэвиджа, Гурвица (γ = 0,3)

 

Решение.

а). Найдем М_i математическое ожидание среднего выигрыша игрока при выборе каждой стратегии, учитывая вероятности чистых стратегий «природы»:

М₁ = 11· 0,3 + 5· 0,2 + 2· 0,1 + (-5) · 0,4 = - 0,47;

М₂ = 14· 0,3 + 6· 0,2 + 8· 0,1 + (-4) · 0,4 = 4,6;

М₃ = 7· 0,3 + (-5)· 0,2 + (-3)· 0,1 + (-5) · 0,4 = - 1,2;

М₄ = 5· 0,3 + 5· 0,2 + (-3)· 0,1 + 3 · 0,4 = 3,4.

Так как М₂ - максимальное математическое ожидание среднего выигрыша игрока, то оптимальной является соответствующая ему вторая стратегия А₂.

 

б). Найдем оптимальную стратегию игрока по критерию Вальда, в основе которого лежит максиминная стратегия нахождения нижней цены игры:

. Найдем минимальный элемент в каждой строке, а из них выберем максимум:

Так как максимин W=-3 соответствует четвертой стратегии А₄, то она и будет оптимальной по критерию Вальда.

Найдем оптимальную стратегию по критерию Сэвиджа. Построим матрицу рисков R, элементы которой равны разности между максимальным элементом столбца и самим элементом столбца:

Так как минимальный из максимальных рисков S=7 соответствует второй стратегии А₂, то она и будет оптимальной по критерию Сэвиджа.

Найдем оптимальную стратегию по критерию Гурвица с коэффициентом пессимизма - оптимизма γ = 0,3. В этом случае необходимо найти в каждой строке линейную комбинацию минимального и максимального выигрышей:

- максимальное значение соответствует второй стратегии А₂, значит она и будет оптимальной по критерию Гурвица.

 

Задание 4. Прокладывается участок пути между пунктами А и В. Весь участок разбит на условные участки по стоимости прокладки пути. Построить план прокладки дороги так, чтобы суммарные затраты были минимальными.

В

А

Решение.

А

В

А

 

Эта задача является задачей Динамического программирования, поэтому ее решение начнем с условной оптимизации, двигаясь с последнего шага к первому. На каждом шаге рассматриваем пункты, от которых до пункта В можно «дойти» за одинаковое число шагов, отмечая стрелочкой направление минимальной стоимости. Само значение минимальной стоимости – условный минимум данного шага – записываем в соответствующий кружочек. Условный минимум первого шага является значением минимальной стоимости прокладки пути от А до В. На этапе безусловной оптимизации, двигаясь от начала к концу, отмечаем направления минимальной стоимости от А до В. Для записи ответа используем следующие обозначения: «с» –вертикальное направление (на «север»), «в» – горизонтальное направление (на «восток»).

Итак, минимальная стоимость прокладки пути – 17 у.е. достигается в следующем направлении – в, в, в, с, с, в, в, с.

 

Задание 5. Найти оптимальное распределение инвестиций между тремя предприятиями в объеме 8 млн. рублей так, чтобы максимизировать сумму прибыли. Зависимость дополнительной прибыли каждого из предприятий от размеров инвестиций указана в таблице:

	П1	П2	П3

 

Решение.

Решение задачи можно выполнить в виде таблицы, используя обозначения:

i - № шага и № предприятия, получающего инвестиции на этом шаге;

S_i - средства для распределения на i – том шаге;

x_i –средства, выделяемые i – тому предприятию;

S_i-x_i - остаток средств для последующего (i + 1) – го предприятия;

F_i (x_i) – прибыль i – того предприятия от вложенных средств;

Z*_i+1(S_i-x_i) – прибыль (i+1) – го предприятия от остатка средств;

Z^*_i – суммарная прибыль данного и последующих шагов.

Решение задачи начинаем с последнего шага, т.к. все оставшиеся к последнему шагу средства должны быть отданы последнему предприятию, и остаток средств должен быть равен нулю. На всех последующих шагах отмечаем условный максимум данного шага и распределение средств, которое к нему приводит. Условный максимум первого шага – максимальная прибыль от вложения заданной суммы. Проводя безусловную оптимизацию от первого шага к последнему, выберем соответствующие распределения средств между предприятиями.

i	Si	xi	Si-xi	Fi (xi)	Z*i+1(Si-xi)	Z*i = F(xi)+Z*i+1(Si-xi)
	2	0
	2	2
	2	4
	2	6
		2	6

 

Максимальная прибыль при распределении инвестиций в 8 млн. руб. составит 17 млн. рублей. При этом первому предприятию следует выделить 2 млн. руб., второму предприятию – 2 млн. руб., а третьему предприятию – 4 млн. руб.

Задание 6. Дана упорядоченная структурно-временная таблица перечня работ по организации выставки-продажи товаров. Требуется построить сетевой график, определить критический путь, критические работы, резервы времени, провести графический анализ комплекса работ по оптимизации сетевой модели по критерию минимума времени Т при заданных ресурсах В. Определить экономию. Построить оптимальный сетевой план работ.

 

Содержание работ	Обозначение, ај	Опорные работы, ај	Коэффициенты пересчёта, сј =1/bј	Длительность работ, ч	Оптим. tј˚
Заказ на оборудование и товары	а1		с1 = 0,1	t1 = 9	?
Разработка системы учёта спроса	а2	-	с2 = 0,2	t2 = 11	?
Отбор товаров и выписка счетов	а3	а1	с3 = 0,3	t3 = 4	?

Поделиться: