ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Определенным интегралом (интегралом по Риману) называется предел интегральной суммы [2]:  ,
,
если он не зависит от способа разбиения отрезка  на части и от выбора точек
на части и от выбора точек  Непрерывная на отрезке
Непрерывная на отрезке  функция
функция  интегрируема.
интегрируема.
Для вычисления определенного интеграла используется формула Ньютона-Лейбница:
 ,
,
где  - первообразная функции
- первообразная функции  .
.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Задание 4. В задачах 4.1 и 4.2 вычислите определенные интегралы, в задаче 4.3 вычислите несобственный интеграл по определению несобственного интеграла или докажите его расходимость.
4.1.  4.2.
4.2.  4.3(1).
4.3(1).  ,
,
4.3(2).  .
.
4. 1. 
Решение.
Первый способ.
Подведем под знак дифференциала функцию sin  :
:
 .
.
Тогда получим

Второй способ.
Используем формулу замены переменной в определенном интеграле: если функция  непрерывна на отрезке [a,b] и
непрерывна на отрезке [a,b] и  - функция, непрерывная вместе со своей производной
- функция, непрерывная вместе со своей производной  на отрезке
на отрезке  , где
, где 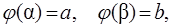 причем сложная функция
причем сложная функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке  , то
, то  .
.
Введем новую переменную:  Тогда:
Тогда: 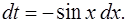 При
При 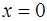
получим  при
при  получим
получим  Следовательно,
Следовательно, 

Ответ:  .
.
Формула интегрирования по частям в определенном интеграле

где  - дифференцируемые на отрезке
- дифференцируемые на отрезке  функции.
функции.
4. 2. 
Решение.
Для вычисления интеграла воспользуемся формулой интегрирования по частям. Положим 
 Тогда
Тогда 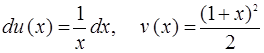 и
и

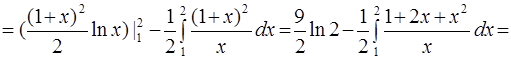

Ответ: 
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫПО БЕСКОНЕЧНОМУ ПРОМЕЖУТКУ (несобственные интегралы первого рода).
Пусть функция  определена и интегрируема на любом отрезке [
определена и интегрируема на любом отрезке [  ]
]  . Несобственный интеграл функции
. Несобственный интеграл функции  по бесконечному промежутку
по бесконечному промежутку  обозначается
обозначается  и определяется как
и определяется как  =
= 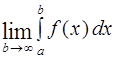
Если предел существует и конечен, то несобственный интеграл называется сходящимся, а функция f(x) - интегрируемой в промежутке  . Если предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.
. Если предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.
Аналогично определяются и другие несобственные интегралы по бесконечным промежуткам:
 ,
,  , где с – любое число.
, где с – любое число.
4.3(1). 
Решение.
Функция  непрерывна на любом отрезке
непрерывна на любом отрезке  По определению несобственного интеграла имеем
По определению несобственного интеграла имеем

Обозначим  Тогда
Тогда  Интегрируя по частям, получим
Интегрируя по частям, получим

Отметим, что 
Ответ: несобственный интеграл сходится и его значение равно: 
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ (несобственные интегралы второго рода).
Пусть функция  непрерывна на промежутке
непрерывна на промежутке  и пусть
и пусть  Несобственный интеграл от неограниченной функции f(x) определяется как
Несобственный интеграл от неограниченной функции f(x) определяется как
 , где
, где 
Если предел существует и конечен, то несобственный интеграл называется сходящимся, а функция f(x) _ интегрируемой на отрезке 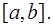 Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся. Аналогично определяются и другие несобственные интегралы от неограниченных функций:
Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся. Аналогично определяются и другие несобственные интегралы от неограниченных функций:
если функция f(x) непрерывна на промежутке  и
и  , то несобственный интеграл определяется так:
, то несобственный интеграл определяется так:
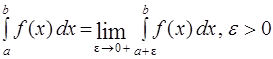 .
.
4.3(2).  .
.
Решение.
Функция  непрерывна на промежутке
непрерывна на промежутке  и
и  . Согласно определению несобственного интеграла имеем
. Согласно определению несобственного интеграла имеем
 =
= 
 .
.
Ответ: несобственный интеграл расходится.
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
В ДЕКАРТОВЫХ КООРДИНАТАХ
Площадь  плоской фигуры, ограниченной прямыми
плоской фигуры, ограниченной прямыми  и непрерывными на отрезке
и непрерывными на отрезке  кривыми
кривыми  , где
, где  , определяется формулой:
, определяется формулой: 
Если  , то получим формулу для площади криволинейной трапеции, ограниченной прямыми
, то получим формулу для площади криволинейной трапеции, ограниченной прямыми  и кривой
и кривой  :
:  .
.
Задание 5. Изобразить области, ограниченные указанными кривыми. С помощью определенного интеграла найти: 5.1.- площадь области, 5.2.1.- объем тела вращения вокруг оси ОХ, 5.2.2. - вокруг оси ОУ.
5.1.  5.2(1).
5.2(1). 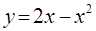 ,
,  ,
,
5.2(2). 
5.1. 
Решение.
Вершина параболы  - точка
- точка  Точки
Точки 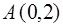 и
и  - точки пересечения параболы
- точки пересечения параболы  и прямой
и прямой 

Рис. 1
На рис.1 изображена область, ограниченная указанными кривыми. Она состоит из двух областей  и
и  , которые можно описать так
, которые можно описать так  :
:  .
. 
 .
.
Согласно правилу вычисления площадей, будем иметь
 .
.
Отсюда 
Ответ:  (кв.ед.).
(кв.ед.).