06сентября
Теория
§ Составьте таблицу умножения ненулевых остатков по модулю 4, 5, 6, 7. Почему в одних таблицах встречаются нули, а в других – нет?
§ Докажите, что если модуль – простой, то в каждой строке и в каждом столбце таблицы умножения остатков все числа различны. (То есть каждая строка таблицы содержит все ненулевые остатки, переставленные в другом порядке.)
§ Докажите, что если р – простое число, и p > а > 0, то: 
§ (Малая Теорема Ферма) Докажите, что если р – простое число и а не делится на р, то 
.
т1. Рассмотрим квадрат, каждую из вершин которого можно покрасить в один из двух цветов: белый или красный. Пусть сначала вершины пронумерованы. Тогда количество различных раскрасок равно 24. Нарисуем на доске все 24.Две раскраски – полностью белая и полностью красная – встречаются по-прежнему один раз. Но у других раскрасок есть «клоны», то есть раскраски, отличающиеся от них только нумерацией. Одну из них можно получить из другой поворотом на некоторый угол. Если мы хотим посчитать количество ненумерованных раскрасок, то это нужно учитывать.
т2. Пусть р – простое число.
а) Сколькими способами можно покрасить вершины правильного p -угольника в n цветов?
б) А если способы, отличающиеся друг от друга поворотом многоугольника вокруг его центра, считаются одинаковыми?
в) Выведите из пункта б) малую теорему Ферма.
т3. Расставим в вершинах правильного р –угольника числа от 1 до p, начиная каждый раз с одной и той же вершины. Докажите, что число различных нумераций равно (p –1)!
т4. Теперь соединим вершины по порядку номеров стрелками, а последнюю соединим с первой. При этом получится несколько замкнутых нумерованных обходов.
а) Докажите, что количество обходов, в которых все стрелки одинаковы,
равно p –1.
б) Докажите, что, если в обходе есть хотя бы две стрелки разной длины, то существует ровно p таких обходов, отличающихся только расстановкой номеров.в) Сотрём номера вершин. Сколько различных «ненумерованных обходов» получилось?
г) Убедитесь, что вы доказали следующее утверждение. Если p – простое число, то (р– 1)!+1 делится на p.
т5. Докажите, что если 
делится на n, то n – простое число.
т6. (Лемма Вильсона) (р– 1)!+1 делится на р тогда и только тогда, когда р – простое число.
т7. Докажите лемму Вильсона, рассмотрев таблицу умножения остатков по модулю p. Докажите, что если р – простое число, то:
а) В каждой строке таблицы умножения остатков встречается ровно одна единица.
б) На диагонали стоят ровно две единицы: в первой и последней строках.
в) Числа 2, 3, 4, …., р –3, р –2 можно разбить на пары так, что произведение чисел в каждой паре будет сравнимо с единицей по модулю р.
г) Докажите, что 
Упражнения и Задачи.
2.1 Найдите остаток от деления: а) 2100 на 101; б) 7102 на 101; в) 8900 на 29.
2.2 Докажите, что 162 п +1 +(2 п +1)16 делится на 17, если 2 п +1 не делится на 17.
2.3 Докажите, что число 30123+12330 делится на 31.
2.4 В десятичной записи трехзначного числа a все цифры различны.
Докажите, что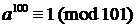 
2.5 Докажите, что если п – натуральное число, не кратное 17, то одно из чисел
п 8 +1, п 4 +1, п 2 +1, п +1, п –1 делится на 17.
2.6 Докажите, что 17120 – 1 делится на 143.
2.7 Докажите, что 33000 – 1 делится на 1001.
2.8 Математические хулиганы Гриша и Вова катаются на лифте 17-этажного дома. Они садятся в лифт на этаже с номером n 
и едут на этаж, номер которого равен остатку от деления n 2 на 17. После этого они умножают на n номерэтажа, накоторомоказались, и едут на этаж с номером, равным остатку от деления на 17 полученного произведения. На каком этаже может закончиться пятнадцатая поездка? А на каком этаже может закончиться седьмая?
2.9 Вове и Грише надоело вспоминать, с какого этажа они начали путешествие, и теперь они просто возводят в квадрат номер этажа, на котором находятся, и едут на этаж с номером, равным остатку от деления результата на 17. Какое максимальное количество поездок удастся им совершить таким способом?
2.10 Пусть p – простое число большее 5. Докажите, что число 777…777 (р –1 семерка) делится на р.
2.11 Преподаватель физкультуры собирается провести зарядку для 47 детей следующим образом. Он даст команду сделать шаг вперед первым 23 школьникам, а затем разместит их между последними 24: первого поставит между 24 и 25, второго – между 25 и 26, третьего – между 26 и 27, и так далее. С получившимся строем он произведёт ту же операцию. Докажите, что после 46-го перестроения дети выстроятся в первоначальном порядке.