Размещения. Понятие факториала.

Выборки и подмножества.

Пусть задано произвольное множество А из n объектов, состоящее из элементов a_i. Последовательность произвольных элементов

< a ₁, a ₂, … a_m >, a_i Î A, i = (1)

называется выборкой объёма m из А, или m -выборкой из множества А, или m -выборкой из n -множества А.

Выясним различие выборки и подмножества.

Дело в том, что в выборке каждый элемент из некоторого множества А может встречаться произвольное число раз, т.е. объём выборки может превосходить объём исходного множества. Если же все компоненты m -выборки из n -множества А различны, то и m -выборка будет представлять собой m -подмножество множества А.

Таким образом, выборка подразумевает возможность наличия в ней одинаковых элементов, а подмножество, как известно из определения множества, не допускает повторений элементов.

Для отличия выборок от подмножеств в формулах для выборок вводят подчёркивание сверху (см. (1)).

Типичный пример выборки – слово в фиксированном алфавите, содержащее одинаковые буквы (например, слово «математика», составленное из букв русского алфавита).

Упорядоченная и неупорядоченная выборки. Кратность элемента.

Если свойства выборки изменяются при транспозиции элементов (т.е. при перемене местами двух элементов), то выборка называется упорядоченной, в противном случае – неупорядоченной. Сравните, например, слова «волос» и «слово», составленные из букв русского алфавита. Упорядоченную выборку из множества десятичных цифр представляет собой телефонный номер, например, 5554433, т.к. номер 5454533 – это уже другой абонент.

Число появлений в выборке одного и того же элемента a_i называют его кратностью и обозначают c(a_i). Если каждый элемент a_i m -выборки имеет кратность c(a_i)=1, то выборка представляет собой m -подмножество множества А.

Понятия размещения, перестановки, сочетания.

Упорядоченное m-подмножество из n -множества называется размещением из n элементов по m, или m -перестановкой из n элементов. Например, у множества, состоящего из четырех элементов а, b, с, d, имеется 24 трёхэлементных упорядоченных подмножества:

abc, abd, acd, bcd,

acb, adb, adc, bdc,

bac, bad, cad, cbd,

bca, bda, cda, cdb,

cab, dab, dac, dbc,

cba, dba, dca, dcb.

 

Размещение из n элементов по n называется перестановкой. Например, у трёхэлементного множества а, b, с число перестановок равно шести: abc, acb, bac, bca, cab, cba.

 

Неупорядоченное m-подмножество из n -множества называется сочетанием из n элементов по m, или m -сочетанием из n элементов. Например, у рассмотренного выше множества, состоящего из четырех элементов а, b, с, d, имеется 4 трёхэлементных подмножества: abc, abd, acd, bcd.

В комбинаторных задачах всегда необходимо подсчитать число всех подмножеств данного множества, удовлетворяющих опреде­лённым условиям, причём в одних задачах подмножества, отличаю­щиеся порядком следования в них элемен­тов, следует считать различными (случай размещений), в других порядок следования элементов не важен, и подмножества, отличающиеся только рас­положением элементов, не считаются различными (случай сочетаний).

Рассмотрим размещения, перестановки, сочетания более подробно.

Размещения. Понятие факториала.

Как определено выше, размещение из n элементов по m – это упорядоченное m-подмножество из n -множества. Число размещений определяется по формуле:

A_n^m = A_{n, m} = , где m = . (2)

А – первая буква французского слова «arrangement», что означает «размещение, приведение в порядок».

Запись n! читается «n - факториал » и представляет собой произведение всех натуральных чисел от 1 до n включительно: n! = 1×2×3´…´ n.

Условились считать, что 0! = 1! = 1. (3)

Тогда по формуле (2), учитывая (3): А ₀⁰ = =1.

А_n⁰ = 1, т.к. существует только одно подмножество n -множества, не содержащее элементов – пустое множество.

Кроме того, принимают А ₀ ^m = 1, хотя А ₀ ^m и не имеет комбинаторного смысла.

 

Задача 1. В классе 30 учащихся. Сколькими способами могут быть выбраны комсорг и староста, если каждый учащийся может быть избран на одну из этих должностей?

Решение.

Выбор Иванова комсоргом, Петрова старостой и выбор Петрова комсоргом, а Иванова старостой – это два различных способа выбора, т.е. имеем случай упорядоченного подмножества: размещения из 30 элементов по 2. По формуле (2):

A²₃₀ = A_{30, 2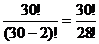} = = 30×29 = 870.·

Число упорядоченных m-выборок из n -множества, т.е. размещений с повторениями, определяется по формуле: 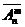= = n^m, .

Задача 2. Абонент забыл последние три цифры телефонного номера. Какое наибольшее число вариантов номеров ему нужно перебрать, чтобы дозвониться (в этом случае необходимый номер набирается последним)?

Решение.

Имеем случай размещения с повторениями из 10 элементов по 3. Действительно, цифра в любой из трёх позиций может быть любая: 0, 1, 2, 3, 4, 5, 6, 7, 8 или 9 (всего 10 вариантов), причём в соседних позициях могут присутствовать одинаковые цифры.

= = 10³ = 1000·

Перестановки.

Размещение из n элементов по n называется перестановкой.

Число перестановок из n элементов обозначают P_n.

Р – первая буква французского слова «permutation», что означает «перестановка».

Из формулы (2), учитывая (3), при m = n получаем формулу для вычисления числа перестановок:

A_nⁿ = A_{n, n} = = P_n.

Задача 3. Сколько вариантов расположения слов допускает предложение: «Редактор вчера внимательно прочитал рукопись»?

Решение.

В данном предложении нет никаких грамматических ограничений на порядок слов, т.е. имеем случай перестановки из 5 элементов по 5.

P ₅ = 5! = 5 × 4 × 3 × 2 × 1 = 120·

Задача 4. Для дежурства в классе в течение недели (кроме воскресенья) выделены 6 учащихся. Сколькими способами можно установить очередность дежурств, если каждый учащийся дежурит один раз?

Решение.

В данной задаче рассматривается шестиэлементное множество дежурных и требуется определить число шестиэлементных подмножеств этого множества, отличающихся друг от друга только порядком следования элементов.

P ₆ = 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720·

Число перестановок с повторениями определяется по формуле:

= n!/(n ₁!× n ₂!´…´ n_k!),

где n_i – число повторений в перестановке элементов i -го типа.

Задача 5. Сколько различных перестановок можно образовать из букв слова «задача»?

Решение.

Поскольку в слове имеются 3 буквы а, перестановки будут происходить с повторениями. Воспользуемся формулой для числа перестановок с повторениями, учитывая, что всего в слове 6 букв, и каждая из букв з, д, ч встречается 1 раз.

= 6 × 5 × 4 = 120·

Сочетания.

Сочетание из n элементов по m – это неупорядоченное m-подмножество из n -множества. Таким образом, сочетания – это совокупности из n элементов по m элементов, которые отличаются друг от друга только самими элементами, но не их порядком следования в совокупности. Число сочетаний определяется по формуле:

С_n^m = С_{n, m} = , где m = .

С – первая буква французского слова «combination», что означает «сочетание».

 

Задача 6. Читатель отобрал по каталогу 8 книг. Однако в библиотеке выдают одному читателю не более 5 книг. Сколько альтернатив взять книги есть у этого читателя?

Решение.

Читатель должен выбрать 5 книг из 8. Все книги разные и всё равно, в каком порядке их взять. Имеем случай сочетания из 8 элементов по 5:

С ₈⁵ = С _{8, 5} = = 8 × 7 = 56·

Задача 7. В турнире принимали участие 4 шахматиста, и каждые 2 шахматиста встретились 1 раз. Сколько партий было сыграно в турнире?

Решение.

Партий было сыграно столько, сколько можно выделить 2-элементных неупорядоченных подмножеств (т.к. каждые 2 шахматиста встречались только 1 раз, и поэтому сочетание Иванов-Петров и Петров-Иванов равнозначны) во множестве из 4 элементов, т.е.

С ₄² = С _{4, 2} = = 2 × 3 = 6.

Если пронумеровать игроков 1, 2, 3, 4, то это были партии 1-2, 3-4, 1-3, 2-4, 1-4, 2-3.·

 

Число неупорядоченных m-выборок из n -множества, т.е. сочетаний с повторениями, определяется по формуле: = = , .

Пример. Кости домино можно рассматривать, как сочетания с повторениями по 2 из 7 цифр: 0, 1, 2, 3, 4, 5, 6. Число всех таких сочетаний равно:

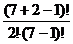= = = 28.

Число всех неупорядоченных подмножеств n-множества определяется по формуле:

N_n = 2 ⁿ.

Задача 8. В комнате 4 светильника. Сколько вариантов включения светильников может быть реализовано?

Решение.

Очевидно столько, сколько существует подмножеств у четырёхэлементного множества, т.е. 2⁴ = 16. При этом учитывается и тот способ «освещения», при котором ни один светильник не горит.

Задачу можно также решить, рассматривая число всех двоичных цифр от 0000₂ до 1111₂, где 0 соответствует, например, выключенному светильнику, а 1 – включённому.·