Формы записи комплексных чисел

Геометрическое изображение комплексных чисел

Всякое комплексное число z=x+ i y можно изобразить точкой М(х;у) плоскости ОXY такой, что х=Rez, у=Imz. И, наоборот, каждую точку М(х;у) координатной плоскости можно рассматривать как образ комплексного числа z=х+ i y (см. рис. 161).

Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа z=х+0 i =х. Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные числа z=0+ i y.

Комплексное число z=х+ i y можно задавать с помощью радиус-вектора r=ОМ=(х;у). Длина вектора r, изображающего комплексное число z, называется модулем этого числа и обозначается |z| или r. Величина угла между положительным направлением действительной оси и вектором r, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Argz или φ.

Аргумент комплексного числа z=0 не определен. Аргумент комплексного числа z≠0 — величина многозначная и определяется с точностью до слагаемого 2πk (k=0,-1,1,-2,2...): Argz = argz + 2πk, где argz — главное значение аргумента, заключенное в промежутке (—π;π], т. е. —π<argz≤π (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0;2π)).

Формы записи комплексных чисел

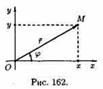Запись числа z в виде z=х+ i y называют алгебраической формой комплексного числа. Модуль r и аргумент φ комплексного числа можно рассматривать как полярные координаты вектора r=ОМ, изображающего комплексное числоz=х+ i y (см. рис. 162). Тогда получаем х=rcosφ, у=rsinφ. Следовательно, комплексное число z=х+ i y можно записать в виде z=rcosφ+irsinφ или z=r(cosφ+ i sinφ).

Такая запись комплексного числа называется тригонометрической формой. Модуль r=|z| однозначно определяется по формуле Например, |i|=Ö(0²+1²)=1. Аргумент φ определяется из формул

Так как φ=Argz=argz+2kπ, то cosφ=cos(argz+2kπ)=cos(argz), sinφ=sin(argz). Поэтому при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного числа z, т. е. считать φ=argz.

Так как -π<argz≤ π, то из формулы tgφ=у/х получаем,что

Если точка z лежит на действительной или мнимой оси, то argz можно найти непосредственно (см. рис. 163). Например, argz₁=0 для z₁=2; argz₂=π

для z₂=-3; arg z₃=p/2 для z₃=i и arg z₄=-p/2 для z₄=-8i.

Используя формулу Эйлера

е^iφ=cosφ+isinφ, комплексное число z=r(cosφ+isiπφ) можно записать в так называемой показательной (или экспоненциальной) форме z=rе^iφ, где r=|z| — модуль комплексного числа, а угол φ=Argz=argz+2kp (k=0,-1,1,-2,2...).

В силу формулы Эйлера, функция е^iφ периодическая с основным периодом 2p. Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа, т. е. считать φ=argz.

 

№14. Комплексные числа. Действия над комплексными числами.

Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, называются комплексными. Число a будем назвать действительной частью комплексного числа, bi – мнимой частью комплексного числа, b – коэффициентом при мнимой части. Запись комплексного числа в виде a + bi называется алгебраической формой комплексного числа. Аргумент комплексного числа – угол между r (в) и положительным направлением ОХ. φ=argz – главное значение аргумента. cosφ=a/r, sinφ=b/r. Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Только учитывают, что i(c.2)= -1, привести примеры. Модулем комплексного числа z = a + bi называется длина вектора, которую можно найти по формуле |z|=√a(c.2)+b(c.2)`. Обозначается буквой r (в). Если в запись комплексного числа z вместо a и b подставить другие значения, то получим z=a+ib=r cosφ +ir sinφ = r (cosφ + i sinφ). Это тригонометрическая форма записи комплексного числа. Показательная форма записи: z=|a|e(c.iφ); Что перейти используем формулу Эйлера: cosφ+isinφ=e(c.iφ).

№15. Линейные диф. уравнения 2-го порядка с постоянными коэффициентами.

В математической экономике большое применение находят линейные дифференциальные уравнения, и поэтому мы рассмотрим решение таких уравнений. Дифференциальное уравнение (9.1) называется линейным, если имеет вид: р_o(x)y⁽ⁿ⁾(x) + р₁(x)y^{(n- 1)}(x) +... + р_{n - 1}(x)y¢(x) + р_n(x)y(x) = f(x), (9.2)

где р_o(x), р₁(x),..., р_n(x), f(x) - данные функции. Если f(x) º 0, то уравнение (9.2) называется однородным, в противном случае - неоднородным. Общее решение уравнения (9.2) есть сумма какого-либо его частного решения y(x) и общего решения соответствующего однородного уравнения:

р_o(x)y⁽ⁿ⁾(x) + р₁(x)y^{(n- 1)}(x) +... + р_{n - 1}(x)y¢(x) + р_n(x)y(x) = 0. (9.3)

Если коэффициенты р_o(x), р₁(x),..., р_n(x) постоянные, то уравнение (9.2) принимает вид:

р_oy⁽ⁿ⁾(x) + р₁y^{(n- 1)}(x) +... + р_{n - 1}y¢(x) + р_ny(x) = f(x) (9.4) и называется линейным дифференциальным уравнением порядка n с постоянными коэффициентами.

Соответствующее уравнению (9.4) однородное уравнение выглядит так:

р_oy⁽ⁿ⁾(x) + р₁y^{(n- 1)}(x) +... + р_{n - 1}y¢(x) + р_ny(x) = 0. (9.5)

Без ограничения общности можно положить р_o = 1 и записать уравнение (9.5) в виде

y⁽ⁿ⁾(x) + р₁y^{(n- 1)}(x) +... + р_{n - 1}y¢(x) + р_ny(x) = 0. (9.6)

Решение уравнения (9.6) будем искать в виде y = e ^kx, где k - постоянная. Имеем: y¢ = k e ^kx, y¢¢ = k² e ^kx,..., y⁽ⁿ⁾ = kⁿ e ^kx_. Подставляя полученные выражения в (9.6), будем иметь:

e ^kx (kⁿ + р₁k^n-1 +... + р_n-1k + р_n) = 0.

Т.к. e ^kx ¹ 0, то kⁿ + р₁k^n-1 +... + р_n-1k + р_n = 0. (9.7)

Равенство (9.7) есть алгебраическое уравнение с неизвестным k. Оно называется характеристическим уравнением для дифференциального уравнения (9.6). Характеристическое уравнение есть уравнение n -й степени, следовательно, оно имеет n корней, среди которых могут быть кратные и комплексные. Если k₁, k₂,..., k_n - действительные и различные корни уравнения (9.7), то - частные решения уравнения (9.7), а общее имеет вид y = .

Рассмотрим подробно линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами: y¢¢ + рy¢ +qy = 0. (9.8)

Его характеристическое уравнение имеет вид k² + рk + q=0 (9.9) и в зависимости от значения дискриминанта D = р² - 4q возможны три случая.

1. Если D>0, то корни k₁ и k₂ уравнения (9.9) действительны и различны, тогда общее решение имеет вид: y = c₁ exр(k₁x) + c₂ exр(k₂x).

2. Если D = 0, т.е. корни k₁ и k₂ действительные и равные, то общее решение находится по формуле:

y = (c₁ + c₂x) exр (k₁x).

3. Если D<0, то корни комплексные, k₁ = a + bi, k₂ = a - bi, где i - мнимая единица. Тогда общее решение таково: y = (c₁ cos bx+c₂ sin bx) exр (ax).

№16. Нахождение оригиналов для изображений с помощью вычетов.

Оригинал f(t) можно найти по формуле обращения, вычисляя интеграл: f(t) =1/(2pi)×ò(от a-i¥ до a+i¥)F(p)e^ptdp вдоль вертикальной прямой Rep=a в полуплоскости Rep>s, где F(p) аналитична (s - показатель роста оригинала). В частности, можно док-ть, что если в остальной части плоскости имеется только конечное число изолированных особых точек р₁,...,p_n и выполняется условие lim (при р®¥)F(p)=0, то f(t) =1/(2pi)×ò(от a-¥ до a+¥)F(p)e^ptdp =å(от k=1 до n)Res F(p)e^pt. (1)

В случае, когда F(p) - рациональная функция (частное многочленов), являющаяся правильной дробью F(p)=A(p)/B(p), то она имеет на всей плоскости только конечное число полюсов (если дробь несократима, то полюсами явл-ся нули знаменателя, а их - конечное число: столько, какова степень знаменателя). Кроме того, условие lim (при p®¥)F(p)=0 выполняется, т.к. степень знаменателя больше. Значит, для такой дроби формула (1) верна: f(t) =å(от k=1 до n)Res A(p)/B(p)×e^pt

Пример 1: F(p)=p/(p²-1)² - правильная дробь, p₁=-1, p₂=1 - полюсы второго порядка.

f(t) =Res(в точке р=-1)pe^pt/(p²-1)² + Res(в точке р=1)pe^pt/(p²-1)² =1/1!×lim(при р®-1)(pe^pt/(p²-1)²×(p+1)²)`<sub>p</sub> + + 1/1!×lim(при р®1)(pe<sup>pt</sup>/(p<sup>2</sup>-1)<sup>2</sup>×(p-1)<sup>2</sup>)`_p =1/2×t×sht.

Оригинал правильной дроби можно найти также, разложив ее на простейшие дроби (методом неопределенных коэффициентов), пользуясь таблицей изображений и линейностью изображений.

Пример 2: F(p) =(3p²+3p+2)/((p-2)(p²+4p+8)) =A/(p-2) + (Mp+N)/(p²+4p+8) =1/(p-2) + (2p+3)/(p²+4p+8); 1/(p-2) ¸e^2t;

(2p+3)/(p²+4p+8) =(2p+3)/((p+2)²+2²) =(2(p+2)-1)/((p+2)²+2²) =2×(p+2)/((p+2)²+2²) - 1/2×2/((p+2)²+2²) ¸ ¸2cos2t×e^-2t - 1/2×e^-2tsin2t; (3p²+3p+2)/((p-2)(p²+4p+8)) ¸e^2t + e^-2t(2cos2t-1/2×sin2t).

№17. Необходимое условие сходимости ряда. Критерий Коши (необходимое и достаточное условие сходимости ряда).

Необходимое условие сходимости ряда (критерий Коши). Для сходимости ряда (1) необходимо и достаточно, чтобы для любого существовало число такое, что при и (n и p – натуральные числа) было выполнено неравенство . В частности, если ряд сходится, то .

Теорема 4: Если ряд сходится, то его общий член стремиться к нулю, т.е. .

Доказательство. По условию ряд сходится. Обозначим через S его сумму. Рассмотрим частные суммы ряда и . Отсюда . Т.к. и при , то .

Условие является необходимым, но не достаточным условием сходимости ряда.

Достаточные условия сходимости рядов. Признак сравнения 1.

Теорема 5: Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена. Доказательство.

Необходимость. Пусть ряд сходится. Это значит, что последовательность его частичных сумм имеет предел. Всякая сходящая последовательность является ограниченной.

Достаточность. Пусть последовательность частичных сумм ряда ограничена. Т.к. ряд

с неотрицательными членами, то его частичные суммы образуют не убывающую последовательность: . Монотонная ограниченная последовательность сходится, т.е. сходится ряд Признак сравнения 2. Теорема 6: Пусть даны два ряда с неотрицательными членами и и для всех n выполняется неравенство . Тогда из сходимости ряда следует сходимость ряда , а из сходимости ряда следует сходимость ряда . Доказательство. Обозначим через и соответственно частичные суммы рядов и . Из неравенства следует, что (7) Если ряд сходится, то по теореме 5 (необходимость) последовательность его частичных сумм ограничена, т.е. для любого n , где М – некоторое число. Но тогда по формуле (7) и , откуда по той же теореме 5 (достаточность) следует, что ряд сходится. Если же ряд расходится, то ряд также расходится, т.к., допустив сходимость ряда получим по только что доказанному сходимость ряда , а это противоречит условию теоремы.

№18. Нули аналитической функции. Ряд Тейлора и ряд Лорана.

Определение. Точка а называется нулём порядка k аналитической функции f (z), если f (a) = f ′(a) = f ″(a) =... = f ^{(k −1)}(a) = 0, но f ^(k)(a) ≠ 0.

Пример. Пусть . Точка a = 0 - нуль этой функции, так как f (0) = 0. Найдём порядок нуля: f ″(z) = − sin z + z, f ″(0)= 0, f ⁽³⁾(z) = − cos z + 1, f ⁽³⁾(0) = 0, f ⁽⁴⁾(z) = sin z, f ⁽⁴⁾(0) = 0, f ⁽⁵⁾(z) = cos z, f ⁽⁵⁾(0) = 1 ≠ 0,. Первая отличная от нуля производная функции в точке a = 0 - пятая, поэтому эта точка - нуль пятого порядка функции .

Теорема. Для того, чтобы аналитическая в точке а функция f (z) имела в этой точке нуль k -го порядка, необходимо и достаточно, чтобы в окрестности этой точки функция f (z) представлялась в виде f (z) = (z − a) ^k · φ (z), где φ (z) - аналитическая в точке а функция, и φ (a) ≠ 0.

Доказательство. Необходимость. Пусть точка а - нуль k -го порядка функции f (z), т.е. f (a) = f ′(a) = f ″(a) =... = f ^{(k −1)}(a) = 0, и f ^(k)(a) ≠ 0. Тогда её разложение в ряд Тейлора имеет вид

, где - аналитическая (как сумма степенного ряда с тем же кругом сходимости, что и у ряда для f (z)) функция, .

Достаточность. Пусть f (z) = (z − a) ^k · φ (z), где φ (z) - аналитическая в точке а функция, и φ (a) ≠ 0. Находим производные этой функции по формуле Лейбница (uv) ⁽ⁿ⁾ = u ⁽ⁿ⁾ v + nu ^{(n - 1)} v ′ + C_n ² u ^{(n - 2)} v ″ + C_n ³ u ^{(n - 3)} v ⁽³⁾ + … + C_n ² u ″ v ^{(n - 2)} + n u ′ v ^{(n - 1)} + uv ⁽ⁿ⁾: f ′(z) = k (z − a) ^{k - 1} φ (z) + (z − a) ^k φ ′(z), f ′(a) = 0; f ″(z) = k (k − 1)(z − a)^{(k - 2)} φ (z) + 2 k (z − a)^{(k - 1)} φ ′(z) + (z − a)^(k) φ ″(z), f ″(a) = 0; …………… ………………………….; f ^{(k -1)}(z) = k ·(k -1)·…2·(z − a) φ (z) + C ¹ _{k -1} k ·(k -1)·…3·(z − a)² φ ′(z) + … + (z − a) ^k φ ^{(k -1)}(z), f ^{(k -1)}(a) = 0;
f ^(k)(z) = k ·(k -1)·…2·1· φ (z) + C ¹ _k k ·(k -1)·…2·(z − a) φ ′(z) + … + (z − a) ^k φ ^(k)(z), f ^(k)(a) = k!· φ (a) ≠ 0, что и требовалось доказать.

Из этой теоремы следует, что если многочлен P _n (z) = a ₀ z ⁿ + a ₁ z ^{n - 1} + a ₂ z ^{n - 2} + … + a _{n - 1} z = 0 разложен на множители P _n (z) = a ₀ (z − z ₁) ^k ₁ (z − z ₂) ^k ₂ … (z − z_l) ^k _l, то корни z ₁, z ₂, …, z_l являются нулями функции P _n (z) кратностей, соответственно, k ₁, k ₂, …, k_l.

Ряд Тейлора. Пусть функция w = f (z) аналитична в области D, z ₀∈ D. Обозначим L окружность с центром в z ₀, принадлежащую области D вместе с ограниченным ею кругом. Тогда для любой точки z, лежащей внутри L, . Представим множитель в виде суммы сходящейся геометрической прогрессии: (так как | z – z ₀| < | t – z ₀|, то ) , и ряд сходится абсолютно, поэтому его можно почленно интегрировать:

, так как . Итак, .
Ряд в правой части этого равенства - ряд Тейлора функции f (z). Этот ряд абсолютно сходится внутри контура L, а в качестве L можно взять любую окружность, которая не выходит за пределы области D. Доказана
Теорема о разложении функции в ряд Тейлора. Если функция w = f (z) аналитична в области D, z ₀ ∈ D, то функция f (z)может быть разложена в ряд Тейлора по степеням (z – z ₀) ⁿ. Этот ряд абсолютно сходится к f (z) внутри круга | z – z ₀| < r, где r - расстояние от z ₀ до границы области D (до ближайшей к z ₀ точке, в которой функция теряет аналитичность). Это разложение единственно.
Единственность разложения следует из того, что коэффициенты ряда однозначно выражаются через производные функции.
19.8.1.1. Стандартные разложения. Для однозначных функций разложения в ряд Тейлора в принципе не могут отличиться от изучавшихся в прошлом семестре разложений:
1.

2. 3. 4. 5. Все эти ряды сходятся к своим функциям на всей плоскости (при ∀ z ∈ C). Для геометрических прогрессий имеют место формулы

7. 8. .
То, что эти ряды сходятся при | z | < 1, понятно. Ближайшие к центру разложения z ₀ = 0 точки, в которых функции теряют аналитичность (граница области D) - это точки z = ±1, в которых соответствующие функции неопределены.

9. .
В действительном случае вообще было непонятно, почему этот ряд перестаёт сходиться к f (x) при | x | ≥ 1, ведь f (x) определена на всей действительной прямой. В комплексном случае это проясняется - на окружности | z | = 1 расположены точки z = ± i, в которых f (z) не определена.
При разложении многозначных функций необходимо выделить однозначную ветвь. Обычно задают значение функции в одной точке. Рассмотрим, например, разложение функции ln(z + 1). Ln 1 = ln 1 + i arg 1 = 2 k π i, k - целое. Возьмём ту ветвь логарифма, для которой Ln 1 = 0 (k = 0), т.е. главное значение логарифма f (z) = ln (z + 1). На этой ветви

, поэтому , и
10.

Точка, в которой функция теряет аналитичность (она в этой точке вообще не определена) - это z = -1, поэтому ряд сходится при | z | < 1.
Теперь рассмотрим биномиальный ряд для функции f (z) = (1 + z) ^α. Это (при любом комплексном α) общая степенная функция, поэтому f (z) = (1 + z) ^α = z ^{α ln(1 + z)} (однозначная ветвь выделена тем, что взято главное значение логарифма); дальше находим производные:

аналогично

f ″(0) = α (α − 1); и т.д.; f ⁽ⁿ⁾(0) = α (α − 1)…(α − n + 1), поэтому
11. .
19.8.1.2. Решение задач на разложение функций в ряд. Техника решения этих задач ничем не отличается от действительного случая (см. раздел 18.2.6.2). Рассмотрим, например, задачу 6 из этого раздела: разложить функцию по степеням z - 7. Так как степень знаменателя равна двум, сначала разложим в ряд функцию , затем почленно продифференцируем его: . Круг сходимости . На границе круга сходимости ряд из модулей расходится, и общий член не стремится к нулю, поэтому в каждой точке окружности ряд расходится. Далее,

. Все выводы о круге сходимости и поведении ряда на его границе остаются справедливыми.
19.8.2. Ряд Лорана. Пусть функция f (z) аналитична в кольце ρ ≤ | z − z ₀| ≤ R. Тогда для любой точки этого кольца ; при этом окружности проходятся так, что область остаётся слева (следствие 3 раздела 19.7.2. Интегральная формула Коши). Изменим в интеграле по внутренней окружности направление обхода на противоположное: . Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора: (так как | z – z ₀| < | t – z ₀|, то ) , и ряд сходится абсолютно, поэтому его можно почленно интегрировать:

, где . Интеграл по внутренней окружности преобразуем аналогично, учитывая только, что на L _ρ | t – z ₀| < | z – z ₀|: . И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать: , где . Переобозначим n → − n, тогда форма коэффициентов ряда для L _ρ совпадёт с формой коэффициентов ряда для L_R: поэтому окончательно для интеграла по L _ρ получим . Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть Γ - кусочно-гладкий контур, расположенный в кольце ρ ≤ | z − z ₀| ≤ R, и точка z ₀ расположена внутри этого контура. По теореме Коши для многосвязной области ; , поэтому для любого n , и

.
Этот ряд (содержащий и положительные, и отрицательные степени (z – z ₀), называется рядом Лорана функции f (z). Его часть, содержащая неотрицательные степени (), называется правильной; часть, содержащая отрицательные степени (), называется главной. Правильная часть, по самому своему построению, сходится в круге | z – z ₀| ≤ R, главная - во внешности круга | z – z ₀| ≥ ρ, поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце ρ ≤ | z – z ₀| ≤ R. Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно.

№19. О постановке задачи математической физики. Краевые и начальные условия и их физический смысл.

В теории дифференциальных уравнений, начальные и граничные условия — дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой области соответственно.

Обычно дифференциальное уравнение имеет не одно решение, а целое их семейство. Начальные и граничные условия позволяют выбрать из него одно, соответствующее реальному физическому процессу или явлению. В теории обыкновенных дифференциальных уравнений доказана теорема существования и единственности решения задачи с начальным условием (т. н. задачи Коши). Для уравнений в частных производных получены некоторые теоремы существования и единственности решений для определенных классов начальных и краевых задач.

Иногда к граничным относят и начальные условия в нестационарных задачах, таких как решение гиперболических или параболических уравнений.

Для стационарных задач существует разделение граничных условий на главные и естественные. Главные условия обычно имеют вид , где — граница области Ω. Естественные условия содержат также и производную решения по нормали к границе.

Задачи математической физики описывают реальные физические процессы, а потому их постановка должна удовлетворять следующим естественным требованиям:

Решение должно существовать в каком-либо классе функций;

Решение должно быть единственным в каком-либо классе функций;

Решение должно непрерывно зависеть от данных (начальных и граничных условий, свободного члена, коэффициентов и т.д.).

Требование непрерывной зависимости решения обусловливается тем обстоятельством, что физические данные, как правило, определяются из эксперимента приближенно, и поэтому нужно быть уверенным в том, что решение задачи в рамках выбранной математической модели не будет существенно зависеть от погрешности измерений. Математически это требование можно записать, например, так (для независимости от свободного члена):

Пусть задано два дифференциальных уравнения: с одинаковыми дифференциальными операторами и одинаковыми граничными условиями, тогда их решения будут непрерывно зависеть от свободного члена, если:

решения соответствующих уравнений.

Множество функций, для которых выполняются перечисленные требования, называется классом корректности. Некорректную постановку граничных условий хорошо иллюстрирует пример Адамара.

№20. Обратное преобразование Лапласа. Разложение оригинала в сумму.

Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Обратное преобразование Лапласа

Обратным преобразованием Лапласа функции комплексного переменного , называется функция действительного переменного, такая что:

где — некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.

На практике приходится искать оригинал, изображение которого представляет собой правильную рациональную дробь.

Известно, что такую дробь можно представить в виде суммы простейших дробей четырёх видов: где корни знаменателя комплексные, то есть дискриминант квадратного трёхчлена, стоящего в знаменателе дроби, отрицателен; корни знаменателя комплексные.

Мы рассмотрим лишь дроби трёх первых видов. Для дроби 1-го вида имеем для дроби 2-го вида на основании формулы (12) таблицы изображений и оригиналов получим:

№21. Общий достаточный признак сходимости знакопеременных рядов. Абсолют. и условная сходимость рядов.

Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости

Пусть u₁+u₂+…+u_n +…= (20) знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов │ u₁ │+│ u₂ │+…+│ u_n │+…= │ u_n │. (21)

Тогда ряд (20) тоже сходится. Доказательство. Рассмотрим вспомогательный ряд (u₁ +│ u₁ │)+(u₂ +│ u₂ │)+…+(u_n +│ u_n │)+…= (u_n +│ u_n │). (22)

Очевидно, 0≤ u_n +│ u_n │≤2│ u _n│ при всех n =1, 2, …. Ряд (21) сходится по условию, поэтому сходится ряд 2│ u_n │, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.

Замечание.

Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться. Например, ряд сходится по признаку Лейбница, а ряд