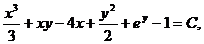Однородные дифференциальные уравнения.
Определение. Функция 
называется однородной функцией 
измерения относительно переменных 
и 
, если при любом 
справедливо тождество: 
Например, функция 
является однородной четвертого измерения 
так как
Определение. Уравнение первого порядка:
называется однородным относительно и , если функция есть однородная функция нулевого измерения относительно и .
Решение однородного уравнения. По условию 
. Положив в этом тождестве 
, получим 
, т.е. однородная функция нулевого измерения зависит только от отношения аргумента.
Уравнения в этом случае примет вид: 
.
Сделаем подстановку 
, т.е. 
, 
.
Подставляя это выражение в уравнение, получим 
это – уравнение с разделяющимися переменными:
,
или
.
Интегрируя, найдем
.
Подставляя после интегрирования вместо 
отношение 
, получим интеграл дифференциального уравнения.
К однородным уравнениям приводятся уравнения вида:
. (1)
Если 
, это уравнение есть однородное. Пусть 
, 
. Сделаем замену переменных 
, 
.
Тогда
.
Подставляя в уравнение (1) выражение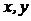 
и 
, будем иметь:
.
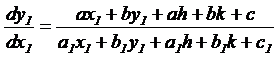Подберем 
и 
так, чтобы выполнялись равенства:
,
т.е. определим и как решения этой системы уравнений. При этом условие данного уравнения становится однородным:
.
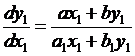Решив это уравнение и перейдя снова к 
и 
получим решение уравнения.
Если 
, то система не имеет решения.
Но в этом случае 
, 
, 
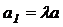и, следовательно, уравнение можно преобразовать к виду:
.
Тогда подстановкой 
уравнения приводится к уравнению с разделяющимися переменными.
Линейные дифференциальные уравнения.
Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Оно имеет вид
, (2.1)
где 
и 
- заданные непрерывные функции от 
(или постоянные).
Решение линейного уравнения находится по формуле
(2.2)
Пример. Найти общее решение уравнения 
Решить задачу Коши при начальном условии у(-2)=2.
Приведем данное уравнение к виду (2.1), разделив обе его части на 
Получим: 
Здесь 
Общее решение исходного уравнения в соответствии с формулой. (2.2) имеет вид
(2.3)
Найдем входящие в это решение интегралы. Имеем
где знаки 
появляются в силу равенства 
Подставляянайденные интегралы в решение (2.3), окончательно получаем общее решение исходного уравнения:
Из него выделяем частное решение, соответствующее начальному условию у(-2)=2:
Полезно иметь в виду, что иногда дифференциальное уравнение является линейным относительно х как функции у,т.е. может быть приведено к виду
(2.4)
Его общее решение находится по формуле
Отметим,что линейное дифференциальное уравнение (2.1) можно также проинтегрировать методом Бернулли, суть которого заключается в следующем. Введем две неизвестные функции u(x) и v(x) по формуле y=u(x)v(x) (подстановка Бернулли). Тогда 
Подставим выражение для 
и 
в уравнение (2.1), получим уравнение 
которое преобразуем к виду
Уравнение Бернулли.
Уравнение вида 
, где и - непрерывные функции от (или постоянные), а 
и 
, называется уравнением Бернулли.
Это уравнение приводится к линейному следующим преобразованием.
Разделив все члены уравнения на 
, получим 
.
Сделаем замену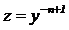 
,
.
Подставляя эти значения в уравнение, будем иметь линейное уравнение:
.
Найдя его общий интеграл и подставив вместо 
выражение 
, получим общий интеграл уравнения Бернулли.
Дифференциальное уравнение
(2.7)
где 
а так же любое уравнение, с помощью алгебраических преобразований приводящееся к уравнению (2.7), называется уравнением Бернулли.
Пример. Найти общее решение уравнения Бернулли 
Так как для данного уравнения 
можно сделать замену 
Получим уравнение 
общее решение которого в соответствии с формулой (7) имеет вид
Общее решение исходного уравнения 
Уравнение в полных дифференциалах.
Уравнение 
называется уравнением в полных дифференциалах, если 
и 
- непрерывные, дифференцируемые функции, для которых выполняется соотношение
,причем 
и 
непрерывны в некоторой области.
Общий интеграл уравнения в полных дифференциалах:
.
Пример. Найти общее интеграл уравнения 
Ведем обозначения 
Так как 
т.е. условие (10) выполнено, то данное уравнение является уравнением в полных дифференциалах. Его общий интеграл можно найти по формуле (11) или (12), положив для простоты 
Выбор этих значений 
, 
допустим, так как функции 
и их частные производные определены, т.е. точка 
По формуле имеем:
По формуле (12) получаем общий интеграл:
