Интервальное оценивание.

2.

Установление статистических закономерностей, присущих массовым случайным явлениям, основано на изучении статистических данных – сведений о том, какие значения принял в результате наблюдений интересующий нас признак (случайная величина Х).

Различные значения признака (случайной величины Х) называются вариантами (обозначим их через х).

Рассмотрение и осмысление этих данных (особенно при большом числе наблюдений n) затруднительно, и по ним практически нельзя представить характер распределения признака (случайной величины Х).

Первый шаг к осмыслению имеющегося статистического материала – это его упорядочение. Расположение вариантов в порядке возрастания (убывания), т.е. ранжирование вариантов ряда.

Пример 1.

В таблице приведена выборка результатов измерения роста 105 студентов (юношей). Измерения проводились с точностью до 1см.

x_min=152, 155,…, 196=x_max

В таком виде изучать рост студентов тоже неудобно из-за большого числа данных. В этом случае варианты разбивают на отдельные интервалы, т.е. проводят их группировку.

Число интервалов m следует брать не очень большим, чтобы после группировки ряд не был очень громоздким, и не очень малым, чтобы не потерять особенности распределения признака. На практике обычно считают, что правильно составленный ряд распределения содержит от 6 до 15 частичных интервалов, однако фактическое число таких интервалов определяется условием задачи.

Согласно формуле Стерджеса рекомендуемое число интервалов m=1+3,322∙lg n, а величина интервала (интервальная разность, ширина интервала) , где х_max-x_min – разность между наибольшим и наименьшим значениями признака.

В нашем примере Примем k=6. За начало первого интервала рекомендуется брать величину или х_min.

Числа, показывающие, сколько раз встречаются варианты из данного интервала, называются частотами (обозначаются n_i), а отношение их к общему числу наблюдений – частостями или относительными частотами, т.е. . Частоты и частости называются весами.

При изучении вариационных рядов наряду с понятием частоты, используется понятие накопленной частоты (). Она показывает, сколько наблюдалось вариантов со значением признака, меньшим х. Отношение накопленной частоты к общему числу наблюдений назовем накопленной частостью . Накопленные частоты (частости) для каждого интервала находятся последовательным суммированием

Определение. Вариационным рядом называется ранжированный в порядке возрастания (или убывания) ряд вариантов с соответствующими им весами (частотами или частостями).

Пример 1. Сгруппированный ряд примера 1 представим в виде таблицы

i	x	ni	wi	niнак	wiнак
	152-158		0,0381		0,0381
	158-164		0,0191		0,0572
	164-170		0,1809		0,2381
	179-176		0,1809		0,4190
	176-182		0,3048		0,7238
	182-188		0,2095		0,9333
	188-194		0,0476		0.9809
	194-200		0,0191
	Σ

Для задания вариационного ряда достаточно указать варианты и соответствующие им частоты (частости) или накопленные частоты (частости).

Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и непрерывным (интервальным), если варианты могут отличаться один от другого на сколь угодно малую величину.

Ряд, представленный в примере 1 является интервальным.

Пример дискретного вариационного ряда является число покупателей в следующей задаче.

Пример 2. В супермаркете проводились наблюдения над числом Х покупателей, обратившихся в кассу за один час. Наблюдения в течение 30 часов дали следующие результаты:

70, 75,100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100

Сгруппируем представленный ряд.

№ гр
Число покупателей
ni
wi	3/30	3/30	7/30	5/30	8/30	4/30
wiнак	0,1	0,2	0,43	0,6	0,87

Перечень вариант и соответствующих им частот называется статистическим распределением выборки. Здесь имеется аналогия с законом распределения случайной величины: в теории вероятностей – это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – это соответствие между наблюдаемыми вариантами и их частотами или частостями. Нетрудно видеть, что сумма относительных частот равна 1, т.е .∑ W_i=1

Весьма важным является понятие эмпирической функции распределения.

Определение. Эмпирическойфункцией распределения F_n(x) называется относительная частота (частость) того, что признак (случайная вличина X) примет значение, меньшее заданного х, т.е.

Эмпирическая функция распределения обладает теми же свойствами, что и функция распределения случайной величины в теории вероятностей:

1) Значения F_n(x) принадлежат отрезку [0; 1];

2) F_n(x) является неубывающей функцией;

3) F_n(x) =0 при x ≤ x_min, F_n(x) =1 при x ≥ x_max.

Наиболее часто вариационный ряды задаются с помощью графического изображения.

Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты (x_i, n_i),i=1,2,…m.

Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака , i=1,2,…m, и высотами, равными частотам (частостям) n_i(w_i) интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.

Помимо полигона и гистограммы рассматривают еще один способ графического задания вариант – кумулятивная кривая – кривая накопленных частот (частостей). Для дискретного ряда кумулята представляет ломаную, соединяющую точки или . Для интервального вариационного ряда ломаная начинается с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте (частости), равной нулю. Другие точки этой ломаной соответствуют концам интервалов.

Пример. Построить полигон (гистограмму), кумуляту и эмпирическую функцию распределения роста студентов и числа покупателей.

 

Пример 1.

 

 

Пример 2.

 

Вариационный ряд содержит достаточно полную информацию об изменчивости признака. Однако обилие числовых данных, с помощью которых он задается, усложняет их использование. В то же время на практике часто оказывается достаточным знание лишь сводных характеристик вариационных рядов. Расчет статистических характеристик представляет собой второй этап обработки данных наблюдений.

 

3.

Одной из основных числовых характеристик ряда распределения (вариационного ряда) является средняя арифметическая.

Существует две формулы расчета средней арифметической: простая и взвешенная.

Простую среднюю арифметическую обычно используют, когда данные наблюдения не сведены в вариационный ряд либо все частоты равны единице или одинаковы , где x_i– i- е значение признака; n – объем ряда.

Если частоты отличны друг от друга, расчет производится по формуле средней арифметической взвешенной , где i -е значение признака для дискретного ряда или середины интервалов интервального вариационного ряда; m_i – частота i- го значения признака; k – число вариантов.

При расчете средней арифметической в качестве весов могут выступать и частости, тогда формула расчета средней арифметической взвешенной примет следующий вид: , где x_i– i-е значение признака; k – число его значений (вариантов).

Найдем среднюю арифметическую по данным табл. примеров 1 и 2.

Решение.

, где 155, 161,…,197 – середины соответствующих интервалов.

Кроме рассмотренных средних величин, называемых аналитическими, в статистическом анализе применяются структурные, или порядковые средние. Из них наиболее широко применяются медиана и мода.

Определение. Медианой Ме вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений.

Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов.

Для интервального вариационного ряда находится середина ряда, а значение медианы на этом интервале находят с помощью линейного интерполирования. Отметим, что медиана может быть приближенно найдена с помощью кумуляты или графика функции распределения как значение признака, для которого = n/2 или =1/2.

Пример.

1) Найдем медиану числа покупателей по данным таблицы примера 2

Решение. n=30 – четное, следовательно, серединных вариантов два: x₁₅=75 и x₁₆=75. Поэтому

Б) Найдем медиану роста студентов (табл.1)

Решение. На рисунке функции распределения и кумуляты проведем горизонтальную прямую у=0,5 (или у=50), соответствующую накопленной частости до пересечения с графиком эмпирической функции распределения (или кумулятой). Абсцисса точки пересечения и будет медианой вариационногоряда: Ме=178

Определение. Модой Мо вариационного ряда называется вариант, которому соответствует наибольшая частота.

Для дискретного вариационного ряда мода равна значению варианты, соответствуюшей наибольшей частоте.

Для интервального ряда находится модальный интервал, имеющий наибольшую частоту, а значение моды на этом интервале определяют с помощью линейного интерполирования. Однако проще моду можно найти графическим путем с помощью гистограммы.

На гистограмме распределения находим прямоугольник с наибольшей частотой (частостью). Соединяя отрезками прямых вершины этого прямоугольника с соответствующими вершинами двух соседних прямоугольников получим точку пересечения этих отрезков (диагоналей), абсцисса которой и будет модой вариационного ряда.

Пример. Найти моды для вариантов примеров 1 и 2.

1) для вариационного ряда примера 2 мода равна 100, так как этому варианту соответствует наибольшая частота равная 8.

2) На гистограмме распределения находим прямоугольник с наибольшей частотой (частостью). Соединяя отрезками прямых вершины этого прямоугольника с соответствующими вершинами двух соседних прямоугольников получим точку пересечения этих отрезков (диагоналей), абсцисса которой и будет модой вариационного ряда: Мо=178.

Колеблемость изучаемого признака можно охарактеризовать с помощью различных показателей вариации. К числу основных показателей вариации относятся: дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Дисперсию можно рассчитать по простой и взвешенной формулам, имеющим вид

Среднее квадратическое отклонение рассчитывается по формуле .

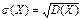Коэффициент вариации определяется формулой

Пример. Рассчитаем показатели вариации для примеров 1 и 2.

Точечное оценивание.

План.

1. Параметрические статистические модели. Точечные оценки. Несмещенность оценки. Состоятельность оценки. Эффективность оценок.

2. Оценка математического ожидания. Несмещенная оценка дисперсии.

1.

Все задачи математической статистики можно разбить на две группы: параметрические и непараметрические. Если известны вид распределения и область изменения параметров, то имеют место параметрические задачи. Например, если известно, что изучаемая случайная величина распределена в совокупности нормально, то необходимо оценить математическое ожидание а и среднее квадратическое отклонение σ², так как эти параметры полностью определяют нормальный закон распределения. Если же закон распределения неизвестен, то речь идет о непараметрической задаче.

Очень часто в приложениях рассматривают именно параметрическую модель. В этом случае предполагают, что закон распределения генеральной совокупности принадлежит множеству {F(x;θ):θ Θ}, где вид функции распределения задан, а вектор параметров θ неизвестен. Требуется найти оценку для θ (приблизительное значение искомого параметра) или некоторой функции от него (например, математического ожидания, дисперсии) по случайной выборке (Х1,Х2,…Хn) из генеральной совокупности Х.

Определение. Оценкой θ_n параметра θ называют всякую функцию результатов наблюдений над случайной величиной Х (иначе – статистику), с помощью которой судят о значении параметра θ: θ_n=θ_n(Х1,Х2,…,Хn).

Т.к. Х1,Х2,…Хn – случайные величины, то и оценка θ_n (в отличие от оцениваемого параметра θ – величины неслучайной) является случайной величиной, зависящей от закона распределения случайной величины Х и числа n.

Существуют два вида оценок: точечные и интервальные. Рассмотрим точечные оценки.

Определение. Точечной оценкой θ* параметра θ называется числовое значение этого параметра, полученное по выборке объема n.

Пусть Х_n =(Х1,Х2,…Хn) – случайная выборка из генеральной совокупности Х, функция распределения которой известна F(х,θ), а θ – известный параметр, т.е. рассматривается параметрическая модель. Требуется построить статистику θ*_n которую можно было бы принять в качестве точечной оценки параметра θ. В общем случае необходимо дать ответ на вопрос: какими свойствами должна обладать статистика θ*_n, чтобы она была в некотором смысле наилучшей оценкой параметра θ. Основное условие, которому должна удовлетворять наилучшая оценка, это, например, математическое ожидание квадрата отклонения оценки от оцениваемого параметра должно быть по возможности меньшим.

Рассмотрим наиболее важные свойства оценок.

Определение. Оценка θ*_n параметра θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е., М(θ*_n)=θ.

В противном случае оценка называется смещенной.

Это свойство желательно, но необязательно. Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.

Хотя каждая отдельная оценка лишь в редких случаях совпадает с соответствующей характеристикой генеральной совокупности, при «аккуратном» оценивании многократное осуществление выборок одного объема n обеспечивает совпадение среднего значения оценки по всем выборкам с истинным значением оцениваемого параметра. Разность М(θ*_n)-θ называется смещением или систематической ошибкой оценивания. Для несмещенных оценок систематическая ошибка равна 0.

Свойство несмещенности оценки является важнейшим, но не единственным. Порой существует несколько возможных оценок одного и того же параметра. Какая из них лучше? Очевидно, выбор будет сделан в пользу той из них, вероятность совпадения которой с истинным значением оцениваемого параметра выше. Оценка должна иметь такую плотность вероятности, которая наиболее сжата вокруг истинного значения оцениваемого параметра, т.е., в этом случае она должна иметь наименьшую среди других оценок дисперсию.

Определение. Несмещенная оценка θ*_n параметра θ называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ, вычисленных по выборкам одного и того же объема n.

Эффективность оценки θ*_n определяют соотношением , где – соответственно дисперсии эффективной и данной оценок. Чем ближе e к 1, тем эффективнее оценка. Если при n , то такая оценка называется асимптотически эффективной.

Определение. Оценка θ*_n параметра θ называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:

.

Другими словами, состоятельной называется такая оценка, которая дает истинное значение при достаточно большом объеме выборки вне зависимости от значений входящих в нее конкретных наблюдений. Свойство состоятельности является обязательным для оценки.

В большинстве случаев несмещенная оценка является и состоятельной. С другой стороны, состоятельные оценки с увеличением объема выборки будут приближаться и лежать все плотнее к истинному значению. Это указывает на асимптотическую несмещенность состоятельной оценки. Поэтому при невозможности получения несмещенной оценки целесообразно найти хотя бы состоятельную оценку.

В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности. Однако этого достичь не всегда удается. Может оказаться, что для простоты расчетов целесообразно использовать незначительно смещенные оценки или оценки, обладающие большей дисперсией по сравнению с эффективными оценками, и т.п.

2.

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя ,

где - варианта выборки; 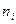- частота варианты ; - объем выборки.

Замечание 1. Если первоначальные варианты - больше числа, то для упрощения расчета целесообразно вычесть из каждой варианты одно и то же число С, т.е. перейти к условным вариантам (в качестве С выгодно принять число, близкое к выборочной средней; поскольку выборочная средняя неизвестна, число С выбирают «на глаз»). Тогда

.

Смещенной оценкой генеральной дисперсии служит выборочная дисперсия

;

Эта оценка является смещенной, так как

.

Более удобна формула

.

Замечание 2. Если первоначальные варианты - больше числа, то целесообразно вычесть из всех вариант одно и то же число С, равное выборочной средней или близкое к ней, т.е. перейти к условным вариантам (дисперсия при этом не изменится).

Тогда .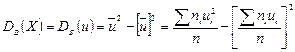

Замечание 3. Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число 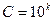, т.е. переходят к условным вариантам 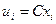. При этом дисперсия увеличится в раз. Поэтому, найдя дисперсию условных вариант, надо разделить ее на :

.

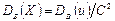Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия

.

Более удобна формула

.

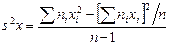В условных вариантах она имеет вид

,

причем если , то ; если , то .

Интервальное оценивание.

1. Интервальное оценивание параметров распределения. Доверительная вероятность и доверительный интервал.

2. Доверительные интервалы для математического ожидания. Оценивание дисперсии в статистике интервальных данных.

1.

После получения точечной оценки θ^* желательно иметь данные о надежности такой оценки. Особенно важно иметь сведения о точности оценок для небольших выборок (поскольку с возрастанием объема выборки состоятельность и несмещенность основных оценок гарантируется утверждениями математической статистики). Поэтому точечная оценка может быть дополнена интервальной оценкой.

Определение. Интервальной оценкой параметра θ называется числовой интервал (θ₁, θ₂), который с заданной вероятностью γ накрывает неизвестное значение параметра θ.

Границы интервала (θ₁, θ₂)и его величина находятся по выборочным данным и поэтому являются случайными величинами в отличии от оцениваемого параметра θ – величины неслучайной, поэтому правильнее говорить, что интервал «накрывает», а не содержит значение θ.

Такой интервал (θ₁, θ₂) называется доверительным, а вероятность γ (уровня значимости α=1-γ) – доверительной вероятностью, уровнем доверия или надежностью оценки. Выбор α или ᵞ определяются конкретными условиями. Обычно используется α=0,1;0,05; 0,01, что соответствует 90, 95, 99%-м доверительным интервалам.

Величина доверительного интервала существенно зависит от объема выборки n (уменьшается с ростом n) и от значения доверительной вероятности γ (увеличивается с приближением γ к единице).

Очень часто доверительный интервал выбирается симметричным относительно параметра θ, т.е. (θ-∆, θ+∆)

Наибольшее отклонение ∆ оценки θ*_n от оцениваемого параметра θ, в частности, выборочной средней (или доли) от генеральной средней (или доли), которое возможно с заданной доверительной вероятностью γ, называется предельной ошибкой выборки.

Ошибка ∆ является ошибкойрепрезентативности (представительства) выборки. Она возникает только вследствие того, что исследуется не вся совокупность, а лишь часть ее, отобранная случайно. Эту ошибку называют случайной ошибкой репрезентативности.

2.

Доверительные интервалы строятся, как правило, в предположении нормальности данных.

Предположим, наблюдается случайная величина . Для параметров строятся следующие точные доверительные интервалы:

1. Для неизвестного среднего 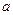при известной дисперсии :

, где определяется из соотношения .

2. Для неизвестного среднего 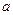при неизвестной дисперсии :

, где - критическая точка распределения Стьюдента (для двусторонней области) с n-1 степенью свободы, на уровне значимости .

3. Для неизвестной дисперсии :

, где и - критические точки - распределения с n-1 степенью свободы и уровнем значимости .

4. По выборке ,…, можно построить доверительные интервалы для следующего (n+1)-го наблюдения (это может быть полезным в качестве прогноза на будущее):

.