Основы проектирования ударного стенда

ВВЕДЕНИЕ

Настоящее издание предназначено для студентов, изучающих курс «Проектирование испытательных стендов» и выполняющих расчётно-графические работы, а также выполняющие курсовое и дипломное проектирование по специальностям 160906, 162110 по направлениям «Экспериментальная отработка» и «Экспериментальная отработка и эксплуатация ЛА».

В задании, выдаваемом студенту на проектирование испытательного стенда, определены следующие пункты: компоненты топлива ЖРД, схема двигательной установки (закрытая, открытая), тяга двигательной установки, время работы двигателя, количество камер сгорания двигательной установки и диаметр ракеты.

При разработке испытательного стенда в рамках курсового и дипломного проектирования ставится задача аргументированного выбора параметров и конструкции испытательного стенда, а также расчета основных геометрических и проектных характеристик испытательного стенда. Решение этой задачи связано с нахождением размеров испытательного стенда; выбором типа форсунок, их числа и схемы расположения на форсуночной головке; расчетом распределения компонентов топлива по сечению смесительной головки и по отдельным типам форсунок; нахождением показателей совершенства камеры сгорания и сопла; оценкой ожидаемых энергетических и массовых характеристик камеры и всей двигательной установки, а также проектированием элементов системы подачи топлива в камеру сгорания.

К настоящему времени накоплен большой практический опыт разработки разнообразных испытательных стендов. Тем не менее, определение основных параметров вновь проектируемого испытательного стенда остается пока делом сложным.

В известных учебниках и учебных пособиях по проектированию испытательного стенда эта проблема в основном рассматривается с общих теоретических позиций; конкретного практического материала и рекомендаций, которые могли бы быть непосредственно использованы при проектировании испытательного стенда, недостаточно. Это создает определенные трудности в учебном процессе, особенно при курсовом и дипломном проектировании.

Данные методические указания, составленные с учетом практического опыта авторов, восполняют в определенных рамках этот пробел.

 

 

Основы проектирования ударного стенда

Основной задачей при проектировании новых или совершенствовании существующих ударных стендов является разработка и создание высоко-производственных и экономических устройств с максимальной интенси-фикацией технологических процессов. Современное проектирование любых испытательных стендов, в том числе и ударных, включает:

- постановка задачи;

- сбор и анализ информации о подобных система и элементах;

- получение исходных данных и условий для работы объектов;

- анализ процессов, связанных с работой испытательной системы;

-составление при необходимости физической или математической модели создаваемой или совершенствуемой системы;

- исследование этой модели с учетом оптимальных показателей и создание новых схем и конструкций испытательного стенда.

Проектирование ударных установок состоит из трех стадий:

- составление проектного задания;

- разработка технического проекта;

- выполнение рабочих чертежей.

Требуемые параметры ударной нагрузки могут быть обеспечены лишь соответствующим выбором условий воспроизведения, в число которых входят объекта v₀ (при заданной массе) в момент начала взаимодействия с тормозным устройством и путь объекта до остановки x_max (путь торможе-ния).

В табл. приведены выражения для v₀, x_max, x_τ типичных импульсов ударного нагружения.

Т а б л и ц а 1

 

Закон n(t) 0 ≤ t ≤ τ	v0	xmax	xτ = v0τ - xmax
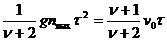
nmax =const	gnmaxτ
1-t/τ			----

 

2. Алгоритм разработки ударного стенда

 

1.1. Исходные данные: M_an, a·b·c, , t, n(t), Ц.М.

 

1.2. Скорость контакта:

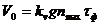, [м/с],

где: k_v – коэффициент формы (0,5…1,0)

Для полусинусоиды – 2/π,

Для треугольной – 0,5,

Для синусквадратной – 0,5,

Для прямоугольной – 1,0.

n_max – максимальная ударная перегрузка,

τ – длительность ударного ускорения (для симметричного импульса длительность фронта τ_ф = 0,5 τ)

 

1.3. Энергия разгонной системы (первое приближение) F_pc/Q_p ≤ 0,1a_max/g

W_треб = M /2 = Q_pH + Q_mcx – A_аэр – F_тр + F_pcHk_n = W_{распол.}, [Дж]

K_n = 0,8 – коэффициент полноты,

= M_ап + М_пл + М_пп + М_рс, [кг]

- суммарная масса подвижных элементов (аппарат, платформа, переходное приспособление, присоединенная масса элементов разгонной системы)

= M_ап + М_пл + М_пп + М_ТС

М_пл = М_ап

М_пп = 0,2 М_ап

М_ТС = 0,1 М_ап

Q_p – вес подвижных элементов на этапе разгона;

Q_ТС – вес подвижных элементов на этапе торможения;

H, x – перемещение разгонной системы и обжатие тормозного устройства (путь торможения);

А_аэр, А_тр – работы аэродинамического сопротивления и трения соответственно;

А_аэр = S_мидH;

A_тр = F_бокf_тр(V₀)Н;

(А_аэр + A_тр) k_д

 

1.4. Перемещение, на котором разгонная система обеспечивает скорость V₀:

H = f (F_рс, n₀, Q_p, Q_mc, x, A_аэр, A_тр), [м],

где F_рс – переменная сила, действующая на этапе функционирования разгонной системы;

n₀ – обратная перегрузка на этапе функционирования РС; n₀ ≤ 0,1 n_max при свободном падении [ м]

1.5. Обжатие тормозной системы:

X_max = k_xV₀τ_ф, [м]

k_x - коэффициент формы (0,5…0,7)

для треугольной – 2/3;

синусквадратной – 0,7;

полусинусоида - 2/π;

прямоугольная – 0,5;

1.6. Максимальная тормозная сила

F_{m max} = gn_max [Н]

= - М_РС - М_ТС, [кг]

М_ТС = 0,1 М_ЛА

 

1.7. Формирование ударного импульса n(t)

Теоретически и экспериментально подбираем динамическую силовую характеристику тормозного устройства F_m(x) [Н/м];

Эмпирическая зависимость ,

а – коэффициент податливости материала, зависит от свойств материала и формы деформируемого элемента. В каждом случае его следует определять экспериментально по кривой ударного процесса;

k – коэффициент, зависящий от формы соударяющихся частей в зоне контакта,

k = 0,6…1,2 (при V=1,5…30 м/с);

- жесткость тормозной системы;

, [c]

Для увеличения τ необходимо увеличить или уменьшить с.

1.8. Разработка рабочих чертежей конструкции стенда, имея переме-щение разгонной системы, обжатие x_max и динамическую (теоретическую) характеристику Fm(x), максимальную тормозную силу тормозной системы F_{m max} (При необходимости производится математическое моделирование).

1.9. Прочностной расчет элементов стенда (платформа, тормозная система, переходное приспособление, разгонная система, ферма, фундамент и т.д.):

· Прочность, устойчивость, срез, изгиб, кручение и т.д.,

· Аварийные ситуации (разрушение аппарата, …)

Выбор расчетных случаев.

1.10. Проверочный расчет характеристик стенда с учетом внесенных конструктивных изменений:

Изм W_потр при V₀ = const

1.11. Подбор и разработка контрольно-измерительной и анализирую-щей аппаратуры (первичные преобразователи, погрешности, основная и вспомогательная аппаратура).

1.12. Разработка методики ударных испытаний:

· Разработка методики измерений;

· Разработка алгоритма обработки результатов.

1.13. Изготовление ударного стенда, курирование изготовления. Корректировка рабочих чертежей и расчета.

1.14. Определение предельных эксплуатационных характеристик стенда.

Изменяя от М_пл до , получаем

V₀(); n(t, ); x_var;

V₀ (n,t) (n_min τ_max) (n_max τ_min).

1.15. Прогнозирование – перенос результатов исследований на эксплуатационные режимы.

 

 

3. Расчет разгонных систем

 

Разгон объекта можно осуществить, используя следующие системы: свободного падения, шнуровую амортизацию, пружины, пневмотолкатели.

При разгоне объекта в результате свободного падения платформа с испытуемым объектом фиксируется на определенной высоте H и затем освобождается, приобретая к моменту соударения скорость

. (3.1.)

Данная скорость будет иметь место без учета потерь сил на трение и аэродинамическое сопротивление. Силы трения определяются с учетом типа выбранного разгонного устройства.

Силы аэродинамического сопротивления при разгоне можно рассчитать следующим образом.

Определив коэффициент лобового сопротивления формы платформы С_х (для платформы, например, прямоугольной формы С_х = 2), можно рассчитать силу аэродинамического сопротивления χ по формуле

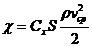, (3.2.)

где S – площадь платформы; v_cp – средняя скорость движения; ρ – плотность среды.

Работа аэродинамических сил сопротивления определится как

А_аэр = χ L, (3.3)

где L – путь движения платформы (при свободном падении L = Н).

Если v₀ – расчетная скорость в конце пути разгона, то фактическая скорость будет v < v₀. Введем такую условную массу m', которую необходимо вычесть из разгонной системы, чтобы скорость в момент удара была расчетной. Тогда с учетом уравнения энергии

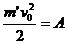_аэр, (3.4)

и уравнения (2.3) можно записать равенство

, (3.5)

и найти условную массу

, (3.6)

Определим среднюю скорость движения v_ср.

Известно, что ускорение , следовательно, , т.е. , где a = n_обg, тогда . Здесь v_н = const – начальная скорость; .

Поэтому можно записать

, (3.7)

где v_max – максимальная скорость в момент окончания разгона (скорость удара): v_max= v₀, т.е.

, (3.8)

Тогда уравнение (2.6) можно записать в следующем виде:

, (3.9)

Следовательно, при определении потерь на аэродинамическое сопротивление необходимо учитывать условную массу m' по отношению к общей массе разгонной системы.

При расчете разгонной системы со шнуровым амортизатором определяется диаметр шнура, количество витков и рабочий диапазон относительного удлинения амортизатора. Рассчитав эти параметры, можно определить путь разгона платформы (т.е. высоту ударного стенда) при условии достижения заданной скорости соударения v₀.

Задаваясь предварительно диаметром шнура разгонной системы при условии, что относительная деформация резиновых шнуров находится в диапазоне 0,2 ≤, ε ≤, 0,8, где ΔL - удлинение шнура, L₀ - длина недеформированного шнура, определяем максимальную F_{ш max} и F_{ш min} нагрузки выбранного шнура (F – сила, создаваема резиновым шнуром).

На ( рис. 1.1 ) показана зависимость силы F, создаваемой резиновыми шнурами, от величины относительного удлинения при разных диаметрах.

Сила, необходимая для создания удара с требуемыми параметрами, определяется

F_max = n_об · M Σ·g, (3.10)

где n_об – обратная перегрузка (n_об = 0,1 n_max); M_Σ - суммарная масса разгоняемой системы.

Число витков требуемого комплекта шнурового амортизатора рассчитывается по следующей зависимости:

. (3.11)

При этом F_ш(ε) выбирается из графика ( рис. 1.1 ).

(Рис.1.1)(Рис.1.2)

 

 

Полученное число витков принимается ближайшим, кратным двум. Работу, совершаемую резиновым разгонным устройством, можно определить по следующей зависимости:

(3.12)

где b – работа одного погонного метра шнура (определяется по графикам при минимальном ε_max и минимальном относительном удлинении ( рис. 1.2 )); l - длина свободного витка разгонной системы (задается таким образом, чтобы максимально уменьшить высоту стенда, но не привысить ε ≥ 0,8).

Ход амортизатора или длина пути разгонной системы L определяется из соотношения

, (313)

Где η - к.п.д. разгонной системы (обычно η = 0,8).

 

Значения F_{ш max} и F_{ш min} определяются по графику (см. рис. 1.1). Варьируя , подбирается заданный закон изменения разгонной силы, т.е. требуемое начальное значение скорости соударения v₀.

Учет сил трения при разгоне необходимо проводить, чтобы с учетом закона F(ε). Для этого воспользуемся средним значением разгонной силы F^СР_РАЗГ, которое определяется по графику (см. рис. 1.1) в пределах 0,2 ≤, ε ≤, 0,8. Для пакетов шнуров из витков

, (3.14)

где F^СР_РАЗГ - среднее значение разгонной силы для одного шнура.

Запишем уравнение энергии:

, (3.15)

где m - условная масса; v₀ - расчетная скорость удара (в конце L); - кинетическая энергия условной массы m, которая равна работе сил трения всей системы при условии, что удар произойдет с расчетной скоростью v₀:

; (3.16)

 

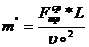. (3.17)

Из условий

. (3.18)

Тогда общая масса системы определяется как

M₀ = M_Σ - m. (3.19)

Расчет разгонного устройства на основе цилиндрических винтовых пружин растяжения-сжатия, с одной стороны, можно проводить по формуле наибольшего касательного напряжения

τ_max = kτ₀,

где ; M_кр – крутящий момент; W_t – геометрический фактор, определяемый размерами и видом сечений.

 

В этом случае можно пользоваться коэффициентом k, который зависит от индекса пружины c = D/d и приближенно определяется по формуле

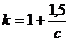, (3.20)

С другой стороны, при расчете пружин на прочность следует руководствоваться формулами:

, (3.21)

τ_max ≤ τ₀,

(3.22)

где [τ] – допустимое напряжение.

Допускаемая нагрузка

, (3.23)

Осевое перемещение

, (3.24)

Диаметр проволоки

, (3.25)

Средний диаметр пружины

D = cd. (3.26)

Для удобства расчетов следует задавать допускаемые значения напряжения [τ] и индекс пружины С. Обычно допускаемое напряжение [τ] для пружин, свитых из проволоки диаметром d ≤ 0,8 мм, задают в зависимости от ее временного сопротивления Gв, т.е. принимают

[τ]= χG _b, (3.27)

где χ – коэффициент, меняющийся в зависимости от класса проволоки и разряда пружин от 0,3 до 0,6.

В случае, когда d ≤ 0,8 мм, вместо формулы (2.15) следует пользоваться соотношением

, (3.28)

Однако, если взять диаметр d из ГОСТ 93-89-75 и установить соответствующую величину σ_в, то можно подсчитать параметр:

, (3.29)

по которому затем определить диаметр пружины:

D = d(ν – 1,5). (3.30)

При расчете разгонной системы с пневмотолкателями принимаются следующие основные допущения:

- потери энергии газа из-за теплообмена со стенками корпуса разгонной системы и трения учитываются путем корректировки работы пневмо-олкателей;

- потери газа через зазоры, деформация стенок корпуса, кинетическая энергия газа и его сопротивления перед поршнем не учитываются.

 

Давление газа в камере пневмотолкателей в процессе ее наполнения при температуре Т_н обозначим Р_н. Температура окружающей среды обычно меняется в определенных пределах и, следовательно, изменяется и давление в пневмотолкателе.

Оценку влияния температуры на изменение давления газа в замкнутом объеме производим с помощью уравнения состояния

p_kw_r = R_rT, (3.31)

где w_r – удельный объем газа; ; - удельный объем газа без учета его полного сжатия.

Учитывая это соотношение и обозначая температуру рабочего газа перед началом движения поршня пневмотолкателя через Т₀, определяем давление газов Рmax в момент начала работы системы:

, (3.32)

Так как тепловые потери рабочего газа через стенки пневомотолкателя не учитываются, то изменение давления р_k подчиняется адиабатическому процессу расширения газа. Для этого процесса справедливо следующее соотношение при движении поршня пневмотолкателя:

, (3.33)

где p_k – давление газа, действующего на поршень в процессе его движения; w – удельный объем газа во время хода поршня: ; γ – показатель адиабаты; α_r – объем, занимаемый единицей веса газа при полном его сжатии.

 

Применив понятие приведенной длины

, (3.34)

представим соотношение

, (3.35)

Подставив (3.25) в уравнение (3.23), с учетом (3.24) получим окончательно

, (3.36)

Силу пневмотолкателя можно определить по формуле

. (3.37)

Работа пневмотолкателя разгонной системы

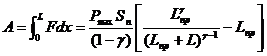, (3.38)

где L – конечное значение хода поршня пневмотолкателя.

 

 

4. Расчет тормозных систем

Расчет тормозной системы с деформируемой шайбой ( рис. 2) позволяет получить большие пути торможения объекта (до 200 – 300 мм) при малых деформациях шайбы. Сила сопротивления, определяющая закон перегрузки, возникает за счет торможения движущейся болванки с конусным наконечником в металлической шайбе, устанвленной на неподвижном основании. Уравнение движения падающих частей может быть записано следующим образом

(4.1)

 

Рис.2

 

Возникновение динамической составляющей силы сопротивления обусловлено, главным образом, зависимостью коэффициента трения от скорости скольжения, а также влиянием динами-ческого нагружения на механические свойства материала шайбы.

Статистические зависимости F_ст (l) для различных пар наконечников и шайб, полученные экспериментально, приведены на (рис. 3). Видно, что в первом приближении функцию F_ст(l) можно считать линейной, т.е.

F_ст (α)= α_т*l, (4.2)

где α_т – коэффициент жесткости тормозного устройства; l – перемещение.

На (рис. 4) показаны зависимости коэффи-циента α_т от угла профильной шайбы Ф _ш (материал наконечника сталь Уl2А, HRC 58-60; шайбы – ст3).

Анализ результатов предварительных ударных испытаний показывает, что зависимость коэффициента трения от скорости можно выразить следующим образом:

 

, (4.3)

где b – эмпирический коэффициент.

(Рис. 3) (Рис. 4)

Поскольку для начальной скорости удара v₀ = 5-20 м⁄с скорость деформации шайбы не превышает (для наконечника конусностью k = 1 - 20) 0,1 … 0,5 м⁄с, следует принять е(v) = 1. Таким образом, уравнение движения принимает вид

 

; (4.4)

 

(4.5)

Интегрируя это уравнения, получаем

(4.6)

При v = 0 максимальный путь торможения

 

(4.7)

 

и, следовательно, максимальная перегрузка

 

(4.8)

 

Скорость v нельзя выразить через l в явном виде и, следовательно, нельзя найти аналитическое выражение для длительности переднего фронта τ. В связи с этим целесообразно уравнение движения решать либо методом последовательных приближений, либо численно.

На ( рис. 5) приведены безразмерные зависимости (t) для различных

(Рис. 5)

Из графиков видно, что v₀ существенно влияет на форму ударного импульса.

Конечные параметры ударного процесса n_max и τ могут быть найдены с помощью вспомогательных функций:

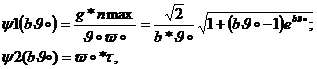{ (4.9)

значения которых определяются в результате решения уравнений движения на ЭВМ.

Создание в лабораторных условиях интенсивных ударных импульсов с большими фронтами возможно при использовании пневматического тормозного устройства.

К числу достоинств пневмодемфера следует отнести его многоразовое действие, а также возможность воспроизведения импульсов различной формы, в том числе и со значительным задним фронтом.

Расчетная схема пневмодемфера приведена на (рис. 6 ). Сила сопротивления, обуславливающая закон n(t), возникает вследствие давления воздуха, сжимаемого в замкнутом объеме при некотором начальном давлении и положении поршня l₀.

(Рис. 6)

При выводе расчетных соотношений примем следующие допущения:

- процесс сжатия адиабатический, поскольку время соударения весьма мало и процессами теплообмена можно пренебречь;

- сила трения при движении поршня в цилиндре и масса падающих частей, а также прорыв воздуха через кольцевой зазор не учитываются;

упругопластические деформации в зоне контакта падающего объекта с тормозным устройством не учитываются.

С учетом указанных допущений уравнение движения платформы с исследуемым объектом будет иметь вид:

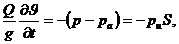(4.10)

где p - текущее значение абсолютного давления в цилиндре; p_a - атмосферное давление; p_и - избыточное давление.

В случае адиабатического сжатия

p = p₀(1-ε)^-γ (4.11)

где γ - показатель адиабаты (для воздуха γ = 1,4); ε - относительное смещение цилиндра и поршня: . Следовательно:

(4.12)

Пренебрегая (3.12), получаем

(4.13)

где v₀ и E₀ - скорость и кинетическая энергия падающих частей в момент начала удара. Из последнего соотношения, приняв v = 0, определим максимальный путь платформы

l_max = l₀ε_max, (4.14)

до полной её остановки:

(4.15)

а также максимальную перегрузку, действующую на объект:

(4.16)

Для определения зависимости элементов движения от времени необходимо вычислить интеграл

(4.17)

Поскольку он не может быть взят аналитически, получить точную зависимость изменения перегрузки во времени n(t) и значение переднего фронта τ (при ε = ε_max) невозможно. В связи с этим можно предложить приближенный метод, который основан на аппроксимации переднего фронта ударного процесса степенной зависимостью

(4.18)

где - начальное значение перегрузки; ν - коэффициент, харак-теризующий форму кривой перегрузки. Решив уравнение движения в виде

(4.19)

можно определить (при t =τ) начальную скорость и максимальное перемещение:

(4.20)

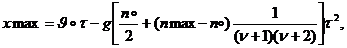(4.21)

откуда нетрудно найти v и τ.

 

 

(Рис. 7)

Расчет гидропневмоамортизатора (на (рис. 7), где 1 – цилиндр, 2 – игла, 3 – уплотнительное кольцо, 4 – поршень, 5 – рабочая жидкость, 6 – редуктор, 7 – запорный вентиль, 8 – манометр МКД, 9 – амортизирующее устройство («наковальня») с резиновой прокладкой) сводится к выводу уравнений, определяющих основные его параметры: давление в гидроцилиндре P1; площадь зазора Sз; диаметр иглы dи. Рабочая площадь поршня (3.22) где D – диаметр поршня (гидроцилиндра); d – диаметр очка (отверстия в конце поршня); D и d задаются. Площадь зазора для протекания жидкости в воздушную полость, регулируемая иглой амортизатора, определяется следующим образом: (3.23) где dи – переменный диаметр иглы, следовательно, Sз = f(t). Учитывая (4.25)

в каждый момент времени

(4.26)

(4.27)

где a_i – это ускорение платформы в каждый i -ый момент времени; v₀ - скорость контейнера в момент встречи с амортизатором; n_max – заданная величина перегрузки; τ - заданное время нарастания перегрузки; t_i - текущее значение времени.

Перетекание жидкости в воздушную полость амортизатора описывается уравнением неразрывности жидкости:

(4.28)

где α - коэффициент сжатия струи жидкости, проходящей через очко поршня; α ≈ 1 (вследствие округления кромок очка); - скорость истечения жидкости через площадь зазора S_a в i -ый момент времени:

(4.29) Умножив обе части на соотношение , получим равенство, определяющее элементарную массу жидкости, проходящую через щель амортизатора за промежуток времени dt:

(4.30)

или

(4.31)

Кинетическая энергия массы будет

(4.32)

или (4.33)

При учете массы перетекающей жидкости уравнение неразрывности характеризуют кинетическую энергию потока, являющуюся мерой работы равнодействующих сил давления жидкости и воздуха, и сил трения уплотнительных устройств и направляющих.

Основное значение имеет только работа сил давления P₁:

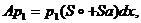(4.34)

а остальные факторы вносят лишь незначительную поправку в расчет, что в конечном счете учитывается при тарировке амортизатора корректированием профиля иглы.

Приравняв правые части уравнения (4.34) и (4.33), найдем

(4.35)

где k_c - корректировочный коэффициент, учитывающий гидравлическое сопротивление струи:

k_c = ζ_c + 1, (4.36)

где ζ - коэффициент сопротивления струи, характеризующей потерю кинематической энергии. Для амортизаторов подобного типа R_c - 1,4…1,6. Учитывая, что P₁S₀ = F_D,

где F_D - сила, вызываемая давлением P₁; Q – вес движущихся частей стенда, получим

(4.37)

После окончания процесса торможения поршень возвращается в начальное положение за счет накопленной энергии сжатого воздуха в полости поршня.

Следовательно, в конечном положении поршня L объем жидкости, попавшей в камеру,

(4.38)

и объем воздуха в полости поршня

(4.39)

где - начальный объем воздуха.

Считая процесс сжатия воздуха политропным, можно определить и другие параметры:

степень сжатия

(4.40)

где P_в.к. - давление воздуха в плотности поршня после сжатия; P_в.0. - давление воздуха в поршне до сжатия; В – показатель политропы;

перепад температуры

ΔT =T₀(N_ν-1 – 1) (4.41)

В зависимости от величины рассчитывается система охлаждения для стенда.

При расчете сплошного цилиндрического амортизатора, для случая осевого сжатия при малых деформациях (менее 20%) в предположении о несжимаемости резины и использовании гипотезы плоских сечений зависимости сила-перемещение может быть представлена в виде P = β₁EFΔ/h, где Δ - величина перемещения, h - высота амортизатора, Е – модуль упругости [Н/м²], F – сечение [м²]. Эта формула получена разными исследователями и нашла широкое распространение в инженерной практике. Для коэффициента β₁ существует ряд соотношений в виде функций, зависящих от безразмерного параметра, характеризующего отношение радиуса к высоте.

В.Л.Бидерман получил формулу

(4.42)

Е.Т.Григорье