В зависимости от вида оператора можно получить ту или иную типовую схему моделирования. Как указывалось, в работе рассмотрены математические модели* применительно к непрерывным и дискретным технологическим процессам. Последние классифицируются в соответствии с теми характеристиками технологического процесса, которые обусловливают применение того или иного математического.аппарата при его моделировании. Рассмотрим следующие виды моделей: стационарные и нестационарные; динамические; линейные и нелинейные; распределенные и сосредоточенные в пространстве; непрерывные и дискретные во времени; непрерывные и дискретные по величине; детерминированные и случайные; информационные.
Стационарные и нестационарные модели. Если свойства преобразования входных сигналов (функций), т. е. структура и свойства оператора 
, не изменяются со временем, то систему и ее модель называют стационарной; в противном случае — нестационарной. Реакция стационарной системы на любой заданный тип возмущения зависит только от интервала времени между моментом начала действия входного возмущения и данным моментом времени, т. е. свойство стационарности означает, что процесс преобразования входных сигналов (функций) инвариантен относительно сдвига входных сигналов во времени. Реакция нестационарной системы зависит как от текущего времени, так и от момента приложения входного сигнала. В этом случае при сдвиге входного сигнала во времени (без изменения его формы) выходные сигналы не только сдвигаются во времени, но и изменяют свою форму.
К стационарным моделям можно обычно отнести и модели одномоментные, используемые в тех случаях, когда моделируется система, для которой необходимо получить какое-то решение в определенный момент времени. Примером могут служить системы управления запасами материалов, в которых одномоментные модели применяются повсеместно (определение однократного объема заказа на пополнение запасов или времени подачи заказа).
Частным случаем стационарных моделей являются модели статические, которые включают описание связей между основным переменными процесса в установившихся режимах (в равновесно состоянии без изменения во времени). Например, математическое описание статики химико-технологического процесса состоит обычно из трех видов уравнений: материального и теплового балансов, термодинамического равновесия системы (характеристика движущей силы) и скоростей протекания процессов (химических реакций, тепло и массопередачи и т. п.). Для расчета медленных процессов или процессов, протекающих с небольшими отклонениями от стабильных условий, принимается допущение, позволяющее считать процесс установившимся. Подобное допущение принимается, например, для расчета теплового баланса турбины при половинной, трехчетвертной либо полной нагрузке или для решения методами линейного программирования задачи смешения материалов.
Стационарные математические модели (кроме статических) обычно состоят из дифференциальных уравнений, статические модели — уравнений алгебраических.
Динамические модели позволяют рассчитать стационарные или не стационарные режимы технологических процессов и других объекты Стандартные динамические модели включают переменные и соотношения между ними:
вектор независимых переменных 
;
добавочную независимую переменную 
, называемую времена хотя она может не представлять физическую временную размерность
вектор неизвестных параметров 
;
вектор переменных 
состояния системы, который является функциями от , и . Эти функции, например, определяются неявно с помощью системы обыкновенных дифференциальных уравнений первого порядка
,
где — вектор заданных функций, и системы начальных условий 
. Здесь 
— вектор заданных функций; вектор наблюдаемых переменных 
, точными значениями которых 
являются заданные функции от переменных состояния и от других переменных:
.
Общеизвестный специальный случай — когда переменные состояния наблюдаются непосредственно, т. е. 
.
Стандартные динамические модели характеризуются множеством переменных состояния системы, которые изменяются со временем (или в зависимости от некоторой другой независимой переменной) в соответствии с определенными дифференциальными уравнениями первого» порядка. Начальные условия могут быть известны полностью или частично. Состояние системы наблюдается в различные моменты времени, но иногда переменные состояния не являются непосредственно измеряемыми, и вместо них приходится измерять связанные с ними наблюдаемые переменные. Неизвестные параметры могут появляться в начальных условиях, в дифференциальных уравнениях и в уравнениях наблюдений. В последнем случае они представляют неизвестные характеристики измерительных приборов, например константы калибровки.
Если в модели объекта содержатся дифференциальные уравнения порядка выше первого, сложность их анализа возрастает с ростом порядка уравнения (или с ростом числа дифференциальных уравнений в системе, поскольку уравнение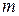 
-го порядка можно преобразовать в систему из 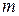уравнений 1-го порядка). Другая трудность, возникающая иногда при анализе систем дифференциальных уравнений, связана с особенностями задания начальных условий. Чаще всего начальные условия задаются при одном и том же значении независимой переменной. Для протекания химических реакций, например, начальными условиями обычно служат значения концентраций в один и тот же момент 
; в описаниях реакторов — это концентрации и температура в одной и той же точке — на входе в аппарат. Задачи с начальными условиями, заданными таким образом, называются задачами Коши. Моделировать их сравнительно просто.
Но встречаются задачи, в которых различные начальные условия заданы в разных точках. Например, во многих аппаратах с противотоком часть условий может быть задана со стороны входа одного потока, часть — со стороны входа другого. Это краевые задачи. Если краевую задачу не удается свести к задаче Коши с помощью дополнительных уравнений (например, уравнений рабочей линии), то решение усложняется. При этом требуется, как правило, применение специальных расчетных приемов — итерации и др.
Состояние системы можно представить как точку с координатами 
в некотором пространстве 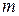измерений, называемом фазовым пространством или пространством состояний. Эта точка называется изображающей. Изменению состояния системы отвечает некоторое движение изображающей точки в этом пространстве. Путь изображающей точки при этом есть интегральная кривая системы. Эта кривая носит название фазовой траектории.
При построении фазового пространства добиваются взаимно однозначного и непрерывного соответствия между состояниями системы и точками фазового- пространства, т.е. каждому состоянию системы должна соответствовать одна и только одна точка фазового пространства, а каждой точке фазового пространства — одно и только одно состояние системы. При этом близким состояниям системы должны соответствовать близкие точки фазового пространства. В силу этих требований фазовое пространство не всегда может быть обычным эвклидовым n-мерным пространством при выполнении на ЭВМ. Благодаря быстродействию и простоте линейные модели широко применяются разработчиками, хотя большинство природных и промышленных процессов — нелинейно. Примером нелинейной модели является зависимость между напряжением и силе тока в электрической цепи, хотя это справедливо в ограниченном диапазоне токов и напряжений.
Лекция 10
Линейность или нелинейность по отношению к входным сигналам — это не то же самое, что линейность или нелинейность выходных переменных (функций) по параметрам. Оператор и задаваемая им модель называются линейными, если для системы справе, лив принцип суперпозиции. Он состоит в том, что линейной комбинации произвольных входных сигналов ставится в соответствие та я линейная комбинация сигналов на выходе из системы:
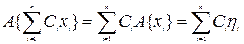
Математическую модель с использованием линейного оператор можно записать в виде 
.
Нелинейные уравнения, в свою очередь, можно разделить на два подкласса: алгебраические (в которых над переменными производите только действия сложения, вычитания, умножения, деления и возведения в степень с рациональным показателем) и трансцендентны, в которые входят другие функции от переменных (показательные, тригонометрические и др.). В любом случае сложность модели существенно зависит от числа уравнений и от вида входящих в них функций. Обычно наиболее просто решаются алгебраические уравнения 1-й степени (линейные), наиболее сложно — трансцендентные.
Линейные и нелинейные модели. Линейность или нелинейность анализируемого процесса оказывает решающее влияние на вид модели, метод программирования и быстродействие программы при ее на практике количество продуктов и уравнений, по которым ведется расчет, составляет несколько сотен, поэтому решение таких задач вручную получить весьма затруднительно.
В моделях производственных процессов, кроме уравнений, могут быть и неравенства.
В математических моделях часто используется ряд нелинейных математических структур, в первую очередь, это степенные полиномы. Методы интерполяции дают возможность существенно упростить способы расчета коэффициентов степенного полинома при наличии точных данных о входных и выходных параметрах. Например, при выборе в качестве математической структуры полинома вида
для данных с равноотстоящими значениями независимой переменной коэффициенты рассчитываются по упрощенному способу:
,
где 
— шаг интерполяции; 
— разность 
-го порядка. В результате полином 
записывается в виде
называется интерполяционным полиномом Ньютона.
В интерполяционном полиноме Ньютона используются раз полученные при движении по одну сторону от значения, взятого качестве начального. При использовании центральных разностей, полученных в результате применения как последующих значений функций (следующих после значения, выбранного в как начального), так и предыдущих, коэффициенты полинома рассчитываются следующим образом:
Введя обозначение 
, получим интерполяционный полином Гаусса для равноотстоящих 
точек интерполяции:
Для неравноотстоящих узлов интерполяции используется интерполяционный полином Лагранжа
Особое место среди известных математических структур занимают ортогональные полиномы. Ортогональным называется полином
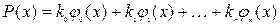
если всякая функция 
системы 
норма и две различные функции и указанной системы функций ортогональны в заданном интервале 
, т.е. имеет место равенство
Подобный выбор функций дает возможность при квадратичном приближении произвести упрощенный расчет коэффициентов 
.
Наиболее часто используют те ортогональные полиномы, для которых легко найти выражение в явном виде. Такими являются, например, приведенные ниже полиномы Чебышева, используемые для промежутка [-1; +1]. Полином Чебышева первого рода определяется выражением
где значения 
определяются по выражению
Для целых положительных значений это выражение является обычным степенным полиномом, так как 
При изменении 
и в промежутке 
используется полином Эрмита
Для периодических функций используются тригонометрические полиномы
Каждая из математических структур обладает своей спецификой, что и определяет область ее применения при моделировании. Интерполяционные полиномы используются для объектов с известными зависимостями или с точными данными о значениях входных и выходных параметров.
Модели распределенные и сосредоточенные в пространстве. Технологический процесс может быть распределенным или сосредоточенным в пространстве и одновременно изменяться во времени. Модели, описывающие распределенные процессы, называются моделями с распределенными параметрами. Обычно они имеют вид дифференциальных уравнений в частных производных. Если основные переменные процесса не изменяются в пространстве, а только во времени, то математические модели, описывающие такие процессы, называют моделями с сосредоточенными параметрами и представляют их в виде обыкновенных дифференциальных уравнений.
Если процесс развивается одновременно и во времени, и в пространстве (по одной координате 
то оператор 
может преобразовывать входную векторную функцию 
в выходную векторную функцию 
и зависеть от обоих аргументов: 
.
Модели непрерывные и дискретные во времени. Непрерывной во времени модель является в том случае, когда характеризующая ее переменная определена для любого значения времени конкретной во времени, — если переменная получен; ко в определенные моменты времени. Непрерывный во времени процесс определяется моделью 
, где может принимать любое значение.
Так, если сигнал 
некоторого компонента системы огибает только в моменты времени 
то такой дискретный сигнал в моделировании записывают в виде последовательности 
. Дискретность модели может также возникнуть в том случае, ее состоит из непрерывных компонентов, но информация переходы одной компоненты к другой по заданной схеме (такие переходы возможны только по окончании соответствующих операций).
Непрерывные модели применяются при изучении систем, с непрерывными процессами, которые описываются с помощью систем дифференциальных уравнений, задающих скорость изменения переменных системы во времени. Непрерывные модели можно описать с помощью конечно-разностных уравнений, которые в предел ходят в соответствующие дифференциальные уравнения. Программирование непрерывных моделей сводится к дискретной вычислительной задаче, которую можно символически записать уравнения
где 
, 
— соответственно векторы состояния с компонентами, определяемыми во все предыдущие моменты в; — вектор внесистемных переменных; — вектор параметры системы; 
— функция, определяющая поведение системы.
Конечно-разностные уравнения (линейные и нелинейные, стационарные и нестационарные, уравнения первого и более высокого порядков, одномерные и многомерные) позволяют описать самые образные динамические системы как с дискретным временем, в пределе, с непрерывным, т. е. это достаточно универсальны моделирования.
Рассмотрим линейное одномерное конечно-разностное уравнения 7-го порядка 
с постоянными коэффициентами. Предположим наблюдения производятся в дискретные, равноотстоящие моменты времени. Примем также, что реакция на выходе такой динамической стационарной системы появляется с некоторой временной задержкой (на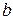 
интервалов квантования) по отношению к входному сигналу. С учетом указанных предположений запишем конечно-разностное уравнение в виде
где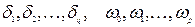 
— параметры уравнения; 
— номер очередного интервала квантования.
Линейное конечно-разностное уравнение высокого порядка подобного типа всегда можно заменить системой конечно-разностных уравнений первого порядка, выраженных в форме Коши, т.е. разрешенных относительно первых разностей. Это обстоятельство привело к тому, что в качестве наиболее общего вида представления математического описания стали широко использоваться конечно-разностные модели в форме Коши. Стационарная линейная система может быть описана моделью в стандартной форме:
где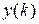 
, 
, 
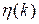— соответственно векторы откликов, переменных состояния и управляющих входных сигналов.
Матрицы 
, 
и 
не зависят от момента времени, т. е. являются постоянными. Они могут включать неизвестные параметры модели, подлежащие оцениванию. Приведенную модель называют также канонической формой модели стационарной линейной системы с дискретным временем. Если система нестационарна, то матрицы , и будут зависеть от .
Нелинейная импульсная система в достаточно общем случае может быть описана моделью
где 
— векторные функции.
Дискретизация возможна не только по аргументу — времени, но и по уровню (величине) сигналов. В этом случае сигналы имеют конечное число значений в некоторой заданной области существования. Подобные сигналы называют дискретными по величине или квантованными. И если непрерывному скалярному сигналу 
соответствует плавная кривая, то квантованному скалярному сигналу отвечает кусочно-постоянная линия (рис).
Рис. Непрерывный 
и дискретный по величине сигналы
Системы (модели), у которых входные и выходные сигналы являются непрерывными по времени и по величине, называют непрерывными. Если же входные и выходные сигналы дискретны по времени, то системы называют системами с дискретным временем или импульсными. Системы, у которых входные и выходные сигналы дискретны или по времени, или по величине, называют дискретными.
Существуют также и системы промежуточного типа, у которых свойства сигналов как функций от времени различны. Например, часть сигналов может быть непрерывной во времени, тогда как остальные сигналы могут быть дискретными. Такая система называется дискретно-непрерывной по времени.
Лекция 11
Детерминированные и случайные модели. По наличию в модели случайных элементов, т.е. в зависимости от способа задания параметров, исходной информации, начальных условий и способа нахождения характеристик системы, математические модели можно подразделить на два больших класса: детерминированные и случайные (вероятностные, стохастические). В детерминированных моделях все исходные данные, ограничения и целевая функция (т.е. некоторое соотношение, количественно характеризующее поставленную перед системой цель) задаются в виде конкретных чисел, векторов или числовых функций.
В детерминированных моделях используются различные классические методы математики: дифференциальные, линейные разностные и интегральные уравнения, операторы для сведения к алгебраическим моделям и др. При совместном рассмотрении этих соотношений состояния системы в заданный момент времени однозначно определяются через параметры системы, входную информацию и начальные условия.
По степени математической абстракции детерминированные модели можно разделить на сложные, описывающие все причинные связи какой-то реальной системы и позволяющие точно прогнозировать поведение системы в зависимости от изменения переменных (или параметров), и упрощенны е,— в которых выбирается ряд основных, существенных зависимостей; устанавливаются и математически описываются связи между отдельными параметрами, соответствующие причинно-следственным закономерностям; другие, несущественные, связи отбрасываются (идеализированные модели).
Между этими двумя моделями существует ряд моделей, отличающихся степенью детализации. Первые модели, являясь наиболее точными и достоверными в чистом виде, из-за сложности не могут широко применяться в моделировании промышленного производства. На практике чаще всего применяются упрощенные идеализированные модели. При этом считается, что имеются существенные и несущественные факторы: существенные учитываются, несущественные отбрасываются. Между принятыми в модели факторами и результирующими показателями устанавливается жесткая детерминированная связь. Широкое распространение идеализированных моделей вызвано их простотой и возможностью логического обоснования.
Любому реальному процессу присущи случайные флюктуации. Однако выбор детерминированной или вероятностной математической модели зависит от того, учитываются ли случайные факторы. Выделение детерминированных моделей в отдельный класс объясняется широким их применением и разнообразием математических методов решения детерминированных задач.
Если хотя бы один параметр модели или ограничительная функция имеет в качестве своих значений случайный вектор или случайную величину, то это случайная (стохастическая) модель. В этом случае под однозначностью определения характеристик моделируемого процесса понимается однозначное определение распределений вероятностей для характеристик процесса при заданных распределениях вероятностей для начальных условий и возмущений.
Стохастический характер модели связан с наличием в объекте и в среде различных неконтролируемых, но существенных факторов, которые можно моделировать статистически. Состояние системы в этом случае 
где 
— случайный процесс, моделирующий имеющуюся неопределенность объекта и среды. Эта неопределенность может быть связана как с быстрым изменением параметров объекта, так и с помехами, накладывающимися на измеряемые;-,качения сигналов на входе и выходе объекта.
Стохастический объект и его модель ведут себя неоднозначно в одинаковых ситуациях, что моделируется случайным вектором , статистические свойства которого должны быть заданы. В простейшем случае 
.
Примером стохастического объекта является любой биологический организм, который в одинаковых условиях ведет себя по-разному. В этом случае описывает поведение объекта, которое строго зависит от внешних условий, а все отклонения от этого регулярного поведения образуют «случайную помеху» .
Переход от детерминированной модели к стохастической осуществляется таким образом, чтобы она отражала в себе случайный характер данных и самой модели. Способ перехода выбирается в зависимости от сведений об изучаемой модели: уверенности в правильности и надежности данных и модели. При этом возможно, что эти сведения ошибочны.
Например, в случае детерминированного безинерционного объекта, когда возмущение и реакция могут рассматриваться как случайные величины и соответственно, математическая модель, описывающая объект, дается в виде условного математического ожидания относительно , т.е. объект описывается уравнением вида
,
где 
— условное математическое ожидание относительно 
— неслучайный закон преобразования.
Так, для усилительного элемента, на входе которого действует случайная величина , выходной сигнал имеет вид
.
В общем случае для стохастических объектов оператор является случайным (например, коэффициенты линейного дифференциального уравнения, весовые функции и т. д.).
Информационные модели. С помощью информационных (процедурных) моделей моделируются сложные устройства и комплексы типа вычислительных машин, радиолокационные станции, системы управления большими промышленными установками, летательными аппаратами и т. д. Функционирование таких систем представляет собой цепь событий, происходящих в дискретные моменты времени и заключающихся в изменении состояний элементов. Дискретное представление пространства и времени обусловливает дискретность фазовых переменных, которыми являются величины, характеризующие состояния элементов. Роль элементов и внутренних параметров выполняют системы и выходные параметры некоторых подсистем. Так, элементами ЭВМ можно считать арифметическое устройство, оперативную память, устройства ввода и вывода и т.п. Фазовые переменные, характеризующие состояния этих элементов, могут принимать только два значения: «занято», если в данный момент устройство работает, или «свободно», если устройство находится в состоянии ожидания. Примерами выходных параметров служат вероятность обслуживания поступивших в систему заявок (сообщений), среднее время простоя в очереди на обслуживание, быстродействие устройства. Для построения математических информационных моделей широко используют математическую логику, теорию массового обслуживания, методы теории автоматического управления.
При анализе сложных промышленных производств особый интерес представляют информационные процедурные модели, а также модели режимов и обеспечения безопасности работы. Информационные процедурные модели определяют содержание, формат и скорость (или частоту) потока информации. Эти модели охватывают также контроль и проверку информации, учет и отчетность по ней, получение разрешений и представление некоторых видов информации, меры предосторожности против потерь информации в аварийных случаях и порядок работы по ее восстановлению при неисправностях или поломкам.
Процедурные модели режимов и обеспечения безопасности работы описывают действия, изменяющие состояние комплекса оборудования предприятия, а также совокупность предписаний об ограничениях, налагаемых на ход работы по соображениям безопасности. К типичным режимам относятся пуск, останов оборудования, изменения нагрузки. При разработке этих моделей человек-оператор рассматривается как составная часть комплекса оборудования; ему отведены следующие функции: обеспечение ввода данных в ЭВМ; слежение за выходными данными с помощью измерительной аппаратуры и ЭВМ; привлечение к работе резервного оборудования в случае неисправности основного; отыскание и устранение ошибок в программе и неполадок в ЭВМ. Эти функции отведены оператору, так как он может выполнять их лучшей с большей экономией средств, чем любая автоматизированная система.
Математические модели каждой отрасли современной технологии делятся по классам соответствующих процессов. Так, по характеру материальных и энергетических связей процессы химической технологии можно разделить на 5 основных классов: 1) гидродинамические; 2) тепловые; 3) диффузионные или массообменные; 4) механические и 5) химические. Каждый из этих классов с учетом целевого назначения и условий реализации в свою очередь делится на типовые процессы.
Лекция 12