Имени адмирала С.О. Макарова

КАФЕДРА СУДОВОЖДЕНИЯ

 

В.В. Афанасьев, В.А.Логиновский

 

Расчет координат

места судна по избыточным навигационным измерениям

 

Учебное пособие по Математическим основам судовождения

 

 

Санкт-Петербург

 

 

Учебное пособие разработано на кафедре Судовождения ГМА имени адмирала С.О. Макарова к.т.н., профессором В.В. Афанасьевым и д.т.н., профессором В.А. Логиновским и предназначено для изучения материала по навигационным функциям и линейных методов обработки навигационной информации при подготовке курсовой работы по дисциплине Математические основы судовождения.

Учебное пособие рассмотрено и утверждено к изданию на заседании кафедры Судовождения, протокол N 9. от 30 апреля 2002 года.

СОДЕРЖАНИЕ

 

 

	Введение
	Теоретические основы определения места судна
1.1	Общие сведения
1.2	Навигационная функция расстояния до ориентира на плоскости
1.3	Навигационная функция пеленга на плоскости
1.4	Навигационная функция горизонтального угла
1.5	Навигационная функция вертикального угла
1.6	Навигационная функция расстояния на сфере
1.7	Навигационная функция разности расстояний на плоскости и сфере
1.8	Навигационная функция прямого и обратного пеленга на сфере
1.9	Навигационная функция высоты светила
1.10	Прямой аналитический расчет координат места судна
	Линейные методы расчета координат места судна
2.1	Линеаризация навигационных функций
2.2	Аналитический расчет координат места судна по двум линиям положения
2.3	Расчет координат при избыточном числе измерений навигационных параметров
2.3.1	Равноточные измерения
2.3.2	Неравноточные измерения
2.4	Априорная оценка точности рассчитанных координат
2.5	Апостериорная оценка точности рассчитанных координат
2.6	Графоаналитический расчет

 

МОС

Введение

 

Курсовая работа «Расчет координат места судна по избыточным навигационным измерениям» выполняется по дисциплине Математические Основы Судовождения (МОС) и имеет целью изучение основ теории навигационных функций и линейных методов обработки навигационной информации, включая классический вариант Метода Наименьших Квадратов (МНК) с применением современного матричного исчисления.

Работа выполняется на листах бумаги формата А4 и включает теоретическую и практическую части.

 

СОДЕРЖАНИЕ курсовой работы:

1. Теоретическая часть.

1.1 Навигационные функции, навигационные параметры и изолинии.

1.2 Прямые аналитические методы расчета координат места судна.

1.3 Линеаризация навигационных функций.

1.4 Расчет координат места судна обобщенным методом линий положения.

1.5 Метод наименьших квадратов в задачах обработки навигационной информации.

1.6 Априорная и апостериорная оценка точности обсервации.

1.7 Графоаналитический вариант расчета координат.

1. Расчетная часть.

2.1 Исходные данные к работе.

2.2 Схема, изображающая навигационные ориентиры и счислимое место судна (в масштабе на листе миллиметровой бумаги формата А4).

2.3 Расчет координат места судна и систематической погрешности измерений Методом наименьших квадратов, (две итерации).

2.4 Априорная оценка точности обсервации.

2.5 Апостериорная оценка точности обсервации.

2.6 Схема, изображающая априорный и апостериорный эллипсы погрешностей обсервации для второй итерации (в масштабе на листе миллиметровой бумаги формата А4).

2.7 Расчет координат графоаналитическим способом (в масштабе на листе миллиметровой бумаги формата А4).

Рекомендуемый список литературы:

1. Баранов Ю.К.,Гаврюк М.И.,Логиновский В.А., Песков Ю.А. Навигация. Учебник для вузов. СПБ, Лань, 1997 г., 512 с.

2. Кожухов В.П., Жухлин А.М., Кондраштхин В.Т., Логиновский В.А., Лукин А.Н. Математические основы судовождения. М., Транспорт, 1993 г., 200с.

3. Груздев Н.М. Оценка точности морского судовождения, М., Транспорт, 1989, 192 с.

4. Ривкин С.С. и др. Статистическая оптимизация навигационных систем, Л., Судостроение, 1976, 280 с.

5. Соболев В.И. Информационно - статистическая теория измерений, М., Машиностроение, 1983, 224 с.

6. Стренг Г. Линейная алгебра и ее приложения, М., Мир, 1980, 454 с.

7. Лоусон И., Хенсон Р. Численное решение задач методом наименьших квадратов, М., Наука, 1986, 232 с.

8. Белявский Л.С. и др. Обработка и отображение радионавигационной информации, М., Радио и Связь, 1990, 232 с.

9. Вульфович Б.А. Методы расчета основных элементов навигационных изолиний, М., Пищевая промышленность, 1979.

10. Каврайский В.В. Избранные труды, т.1, 2,Л., УГС ВМФ, 1953.

11. Кондрашихин В.Т. Определение места судна, М., Транспорт, 1989, 229 с.

12. Кондрашихин В.Т. Теория ошибок, М., Транспорт, 1969.

13. Попеко Г.П., Соломатин Е.П. Навигация. Курс кораблевождения, т.1, Л., УГС ВМФ, 1961.

14. Красавцев Б.И. Мореходная астрономия, М., Транспорт, 1986,

15. Статьи в журналах “Записки по гидрографии”, сборник “Судовождение”,ГМА им. адм.С.О.Макарова; “Навигация и гидрография, ”Navigation (США, Великобритания, Франция, Германия).

 

Образец титульного листа:

 

 

	Министерство Транспорта Российской Федерации Государственная Служба РОСМОРФЛОТ ГМА им. адмирала С.О. Макарова Кафедра Судовождения     Курсовая работа на тему РАСЧЕТ КООРДИНАТ МЕСТА СУДНА ПО ИЗБЫТОЧНЫМ НАВИГАЦИОННЫМ ИЗМЕРЕНИЯМ   Работу выполнил __________ Иванов И.И. (С-111) подпись Работу проверил __________ проф. Петров П.П. подпись     Санкт-Петербург

 

 

В конце курсовой работы необходимо вставить 2 чистых листа формата А4, которые будут использоваться при защите.

Вычисления в курсовой работе производятся с полной разрядной сеткой калькулятора, если же для расчета применялся компьютер, то при защите работы курсант должен показать умение применять использованное программное обеспечение.

 

Теоретические основы определения места судна

Из этой главы вы узнаете, что такое навигационный параметр, навигационная функция, навигационная изолиния, и как они используются для определения координат места судна,а также познакомитесь с важной характеристикой навигационной функции - ее градиентом.

1.1 Общие сведения

Счисление пути судна с помощью автономных средств навигации (лаг, гирокомпас), кроме важного преимущества, которое заключается,непосредственно в автономности определения счислимых координат, обладает и существенными недостатками. Эти недостатки характеризуются погрешностями курсоуказателей (компасов) и относительных измерителей скорости (лагов). На показания лагов влияют гидрометеорологические факторы (ветер, волнение, течение, качка). Погрешности счисления растут во времени, снижая точность счислимых координат. Для их компенсации применяют внешние измерения, на точность которых указанные факторы влияния не оказывают. С помощью таких измерений можно получить координаты места судна, которые называются обсервованными, а сама процедура получения координат называется обсервацией. Таким образом координаты места судна могут быть счислимыми и обсервованными. В большинстве случаев обсервованные координаты точнее счислимых, хотя бывает и наоборот.

Для определения обсервованных координат с помощью различных навигационных средств измеряются навигационные параметры (НП).

НП -это линейные или угловые величины, функционально зависящие от координат места судна и координат навигационных ориентиров.

 

 

Именно эта функциональная математическая зависимость и позволяет решить задачу определения места судна (ОМС). Навигационные ориентиры являются обычно точечными.

Наиболее распространенные навигационные параметры:

• Дистанция до ориентира (D)
• Пеленг на ориентир (П). Здесь под пеленгом понимается истинный пеленг (ИП), но для упрощения записей в сокращении будем использовать букву П.
• Горизонтальный угол между двумя ориентирами (a)
• Вертикальный угол ориентира (b)
• Разность расстояний до двух ориентиров (D D)
• Высота светила (h)

Множество НП образует скалярное поле этих параметров на поверхности Земли, и так как координаты навигационных ориентиров известны, то множество значений НП определяют навигационную функцию (НФ), т.е. зависимость НП от координат места судна.

	НФ- это математическая зависимость НП от координат места судна

 

В литературе по морской навигации НП обозначается буквой U, и тогда выражение для навигационной функции в общем виде может быть записано так:

U=f(j,l), (1.1)

Или в локальной системе координат:

U=f(x,y). (1.2)

Если же зафиксировать навигационный параметр U=U₀=const, то получим уравнение навигационной изолинии (НИ):

U₀=f(j,l)=const (1.3)

	НИ- это геометрическое место точек равных значений навигационных параметров

 

Важнейшей характеристикой навигационной функции является ее вектор-градиент g, который характеризует максимальную скорость изменения навигационной функции, или что одно и то же, скорость изменения навигационного параметра, в конкретной точке. НП меняется быстрее всего в направлении n, которое перпендикулярно касательной к навигационной изолинии в точке C. Другими словами, говорят, что градиент направлен по нормали n к НИ. Направление градиента g условно принимается в сторону увеличения навигационного параметра.

	Градиент навигационной функции - это вектор максимальной скорости изменения НФ в конкретной точке поля навигационных параметров, который направлен по нормали к навигационной изолинии в сторону увеличения НП.

 

 

Для вычисления этой скорости, т.е. модуля вектора градиента, необходимо вычислить производную от НФ по нормали n:

(1.4)

Запишем формулы для расчета g (здесь g – обозначение вектора, а g – его модуля).

В локальной прямоугольной системе координат g может быть представлен в виде двухкомпонентного вектора следующим образом:

, (1.5)

и тогда его модуль рассчитается по теореме Пифагора:

(1.6)

здесь , - проекции вектора g на координатные оси, а его направление определится так:

(1.7)

На рисунке 1.1 представлена иллюстрация формул (1.3)-(1.7):

1.2 Навигационная функция расстояния до ориентира на плоскости

Рассмотрим измерения навигационного параметра D, которым является расстояние до навигационного ориентира А. Это расстояние определяется дальномерными навигационными приборами. Одним из таких очень приборов является радиолокационная станция (РЛС).

С учетом практической точности решения навигационных задач на земной сфере (см. главу Сферическая тригонометрия), плоскость в качестве локальной модели земной поверхности можно использовать на расстояниях до 120-180 (?) миль от ориентира.

На рисунке 1.2 представлена навигационная функция расстояния D(x,y) в виде поля навигационных изолиний, которые представляют на плоскости концентрические окружности с радиусом D и с центром в точке расположения навигационного ориентира А. Эти окружности в морской навигации называются изостадии.

Аналитическое выражение для навигационной функции на плоскости с началом координат в точке А запишем в традиционном виде так, см. рис 1.3:

(1.8)

а для вычисление модуля и направления градиента расстояния g _D в счислимой точке С воспользуемся формулами (1.1.5)-(1.1.7):

(1.9)

Результаты вычислений по формулам (1.9) очевидны, что подтверждает их справедливость.Вычислительная модель адекватна реальной ситуации. Выражение в квадратных скобках – не что иное, как счислимое расстояние D _C от счислимой точки С до ориентира А. Модуль градиента расстояния безразмерен и он направлен по линии пеленга П в сторону увеличения дистанции D. Знак «+» при определении t_D принимается, если П< 180⁰; а знак «-», если П>180⁰ .

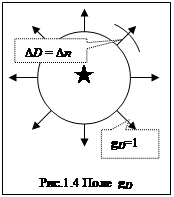
Иллюстрация векторного поля градиентов навигационной функции D (x,y) представлена на рис. 1.4, из которого так же видно, что перемещение по линии пеленга от ориентира, т.е. по нормали n к изостадии на величину D n равно такому же изменению расстояния D D до ориентира.

 

 

1.3 Навигационная функция пеленга на плоскости

Рассмотрим широко применяемую в навигации навигационную функцию пеленга на плоскости. Пределы использования локальной плоскости для моделирования земной поверхности описаны в учебнике [2]. В качестве приборов, измеряющих пеленг используются компасы и РЛС, в которую так же встроен репитор гирокомпаса.

На рисунке 1.5 представлена графически функция пеленга в виде множества навигационных изолиний – линий пеленгов на навигационный ориентир А. При движении по такой изолинии пеленг на навигационный ориентир остается всегда постоянным.

Для вывода формулы градиента рассмотрим рисунок 1.6 и напишем выражение для тангенса пеленга, а затем и для навигационной функции:

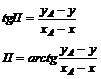(1.10)

Для вычисление модуля и направления градиента расстояния g _П в счислимой точке С воспользуемся опять формулами (1.1.5)-(1.1.7).

(1.11)

После вычислений по формулам мы видим, что модуль градиента пеленга является величиной, обратной расстоянию до пеленгуемого ориентира, или иначе, чем дальше находится ориентир тем медленнее меняется пеленг на него. Это свойство является важным и влияет на точность определения места.

Направление градиента для прямого пеленга выбирается перпендикулярно линии пеленга, т.е. по нормали в сторону увеличения пеленга- нетрудно увидеть, что если судно будет перемещаться по направлению t относительно меридиана, то пеленг на ориентир А будет увеличиваться.

Если D выражено в милях, то единицы модуля градиента (1.11) - «радиан на милю» (1/миля). Если же пеленг выражен в градусах или других единицах, то соответствующую размерность имеет и градиент, например по формуле (1.12) расчет модуля производится в единицах «⁰ / миля».

(1.12)

Если же для решения навигационной задачи используется обратный пеленг, т.е. с ориентира на судно, то естественно, что направление его измениться по сравнению с прямым пеленгом на 180⁰, т.е. для обратного пеленга:

t_П=П+90, (1.13)

а модуль вектора может быть рассчитан по тем же, приведенным выше формулам.

Примерная иллюстрация поля градиентов пеленга представлена на рисунке 1.7.

 

 

1.4 Навигационная функция горизонтального угла

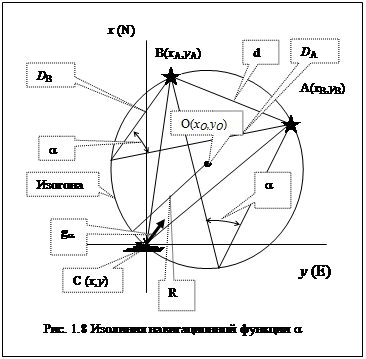Одним из самых точных методов классической навигации является метод определения места по горизонтальным углам. Измерения в этом методе проводятся с помощью секстана или пеленгатора компаса и навигационная функция определяется навигационным параметром a- горизонтальным углом между двумя навигационными ориентирами A и B, рис.1.8.

Расстояние между ориентирами d –называется базой.

Навигационной изолинией, вмещающей измеренный угол является окружность с центром в точке О, которая в навигации называется изогоной. При решении задачи ОМС на плоскости –это плоская изогона.

Уравнение семейства окружностей, вмещающей горизонтальные углы a, т.е. уравнение НФ в неявном виде запишется так:

(1.14)

Преобразуем (1.14) относительно навигационного параметра a и получим выражение НФ в явном виде:

(1.15)

Для дальнейших выводов можно воспользоваться формулами (1.1.5)-(1.1.7), но покажем несколько иной подход вывода формул градиента.

Угол a можно получить, как разность двух пеленгов на ориентиры A и B:

a=П_A-П_B, (1.16)

и тогда справедливо векторное равенство:

g _a= g _ПА- g _ПB, (1.17)

или в векторно-матричных обозначениях:

(1.18)

Подставляя в (1.18) выражения из (1.11) для частных производных пеленга и применяя к треугольнику ABC на рис.1.7 теорему косинусов для плоского треугольника, получим следующие выражения для горизонтального угла:

(1.19)

 

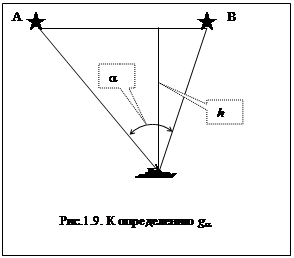
Еще одна формула для градиента g _a, применяемая в навигации для анализа геометрических и точностных характеристик имеет следующий вид, см. рисунок 1.9:

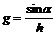(1.20)

 

Градиент направлен к центру изогоны по направлению t.

Как видно из рис.1.10, где представлены изолинии навигационной функции горизонтального угла, при приближении к ориентирам скорость изменения функции увеличивается (изолинии становятся гуще), т.е. модуль градиента растет.

Примечательно, что если ориентир находится вблизи северного географического полюса то пеленг П может считаться горизонтальным углом a между полюсом и навигационным ориентиром, и он измеряется с помощью пеленгатора компаса.

 

 

 

1.5 Навигационная функция вертикального угла

Если высота навигационного ориентира известна, то измерив с помощью секстана его вертикальный угол b, можно рассчитать расстояние до ориентира. В данном случае навигационным параметром является угол b, навигационная изолиния-окружность, а навигационная функция может быть записана так, см. рис. 1.11:

(1.21)

Угол b пересчитывается в другой навигационный параметр, это расстояние до ориентира D:

 

(1.22)

Для получения формул градиента функции (1.21) воспользуемся применявшимися ранее формулами:

 

(1.23)

 

Анализ формул (1.23) позволяет сделать вывод, что модуль вектора градиента вертикального угла увеличивается при приближении к навигационному ориентиру, а его направление совпадает с пеленгом на ориентир. На рисунке 1.12 представлена навигационная функция b в виде сетки изолиний, проведенных через равные промежутки Db. Как видим «густота» сетки увеличивается с приближением к ориентиру, увеличивается скорость изменения навигационного параметра, т.е. модуль градиента функции. В районе A градиент больше, чем в районе B. Кстати, все навигационные функции обладают таким свойством, за исключением тех, у которых модуль градиента равен единице.

 

 

1.6 Навигационная функция расстояния на сфере.

При измерении больших расстояний навигационная функция должна быть представлена на сфере. Это можно сделать, обратившись к рисунку 1.13. Тогда из сферического треугольника АP_NС по теореме косинуса стороны получим следующее уравнение навигационной функции:

D=arccos(sinj_A sinj+cosj_AcosjcosDl)

(1.24)

Навигационной изолинией в данной ситуации является малый круг на поверхности сферы, который имеет сферический радиус D и называется сферической изостадией.

Очевидно, что по аналогии с плоской изостадией: g=1, t=П ±180.

 

1.7 Навигационная функция разности расстояний на плоскости и сфере

Навигационный параметр и функция разности расстояний от судна до двух ориентиров описывают семейство изолиний, которые называются гиперболами. Функция используется в качестве геометрической основы разностно- дальномерных радионавигационных систем, таких как «Лоран-С» и «Чайка».

С точки зрения математики гипербола- это геометрическое место точек постоянной разности расстояний DD до двух ее фокусов. В этих фокусах находятся навигационные ориентиры, до которых измеряется разность расстояний.

На рис. 1.14 показаны навигационные ориентиры A (x_A, y_A) и B (x_B, y_B). Из текущей точки C(x, y) до них измерена разность расстояний DD =D_A-D_B. Эта разность расстояний постоянна на изолинии, которая называется гиперболой. Линия, соединяющая навигационные ориентиры называется базой. Из тоски C(x, y) база видна под углом w, который называется базовым углом.

Запишем функции расстояний, используя формулу (1.8):

, (1.24)

тогда навигационная функция D D запишется так:

D D=D_A-D_B (1.25)

 

В соответствие с (1.8), (1.9) и (1.25) формула для градиента функции может быть представлена в вектороном виде:

 

(1.26)

Модуль его расчитаем по теореме Пифагора:

 

(1.27)

Направление градиента определиться в соответствие с (1.7):

(1.28)

 

Анализ (1.27) показывавет, что при удалении от базы модуль градиента разности расстояний уменьшается. Поле гипербол показано на рис. 1.15.

Применяя формулу косинуса стороны сферического треугольника, запишем навигационную функцию.

(1.29)

На сфере гипербола представляется замкнутой кривой, см. рис. 1.16. Модуль градиента g и его направление t определится по формулам (1.27) и (1.28).

 

 

 

1.8 Навигационная функция прямого и обратного пеленга на сфере

При пеленговании на сфере различают два случая:

1. с судна пеленгуется навигационный ориентир А, т.е. измеряется прямой пеленг П (обратная радиозасечка)
2. с ориентира пеленгуется судно С, т.е. измеряется обратный пеленг B (прямая радиозасечка)

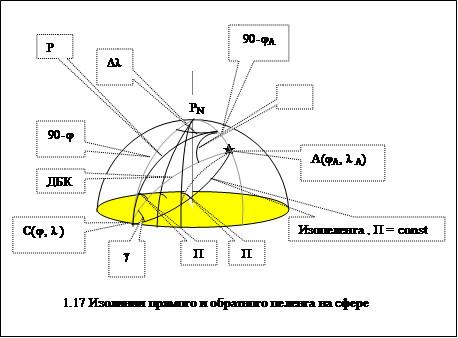В случае (a) прямого пеленгования навигационного ориентира с судна на больших расстояниях навигационная функция может быть получена средствами сферической тригонометрии. На рис.1.17 навигационный ориентир А пеленгуется из точки С. Если мы хотим двигаться так, чтобы навигационный параметр П на ориентир А всегда был постоянен, то необходимо следовать по некоторой кривой, которая называется изопеленгой или изоазимутой. Эта кривая показана на рисунке яркой линией и в любой ее точке угол П между нордовой частью истинного меридиана и направлением на ориентир (дуга большого круга) будет постоянным.

Если же судно запеленговано с помощью пеленгаторной станции (b), то изолинией постоянного пеленга B с ориентира на судно будет ДБК (ортодромия), которая по кратчайшему расстоянию соединяет точки А и С. Обе кривые в точке А и в точке С по разному ориентированы относительно меридиана и эта разница определяется углом g, который равен сферическому схождению меридианов.

В обоих случаях уравнения навигационных функций может быть получено из сферического треугольника P_nAC по теореме котангенсов:

(1.30)

Для случая (a):

(1.31)

Для случая (b):

(1.32)

В (1.32) задаваясь координатами навигационного ориентира, величиной ортодромического пеленга B, и долготой судна, имеем возможность вычислять широту точек ортодромии.

Параметры градиентов можно получить используя традиционные приемы, показанные выше. Мы приводим готовые результаты, известные в литературе по навигации:

a. g _П=sinП/tgP, t=П-90+g (1.33)

b. g _B=1/sinD, t=B+90+g (1.34)

 

Здесь P- сферический перпендикуляр, опущенный из точки С на меридиан точки А; D= АС- расстояние от точки А до точки С по ортодромии.

 

1.9 Навигационная функция высоты светила

Навигационным параметром для определения места по небесным светилам является высота светила h измеренная над плоскостью истинного горизонта с помощью секстана, а навигационная изолиния- это малый круг на поверхности Земли, принятой за сферу – круг равных высот. С точки геометрии измерению h можно сопоставить измерение вертикального угла b (параграф 1.5), и различие заключается в том, что светило находится на бесконечном,с точки зрения практической навигации расстоянии от Земли, а задачу определения места судна необходимо решать на сфере, а не на плоскости. Получить все аналитические зависимости можно с помощью формул сферической тригонометрии,и существенным здесь является то, что сам радиус сферы никак не задействован в этих формулах, а поэтому для фиксации положения наблюдателя и положения светила можно использовать земную сферу.

Выведем формулу навигационной функции h, а для этого обратимся к рис. 1.18. На рисунке представлена Северное полушарие Земли. В точке S(d, t_гр) находится небесное тело. Здесь d, t_гр- координаты светила, которые являются полной аналогией географических координат. Фактически на некоторой воображаемой концентрической Земле сфере (Небесная сфера) d=j, а t_гр=l. С помощью центрального проектирования светило S(d, t_гр) перенесено на поверхность Земли в точку S’(d, t_гр). Наблюдатель находится в точке C₁(j,l) или в любой другой точке C_i(j,l), из которых над горизонтом измерен навигационный параметр h. В точке C₁(j,l) показана плоскость истинного горизонта (касательная плоскость), проведена нормаль к поверхности, указывающая на зенит. Угол z между нормалью и направлением на светило называется зенитным расстоянием. В соответствии с рисунком h + z = 90. Светило видно под углом h к горизонту не в одной точке, а на некоторой кривой, все точки которой равноудалены от проекции светила S’. Этот малый круг с полюсом в точке S’ – круг равных высот.

Рассмотрим сферический треугольник P_nS’C_i. В этом треугольнике сторона C_iS’= z =90- h, так как точка C_i - проекция зенита Z на земную сферу. Теперь по теореме косинуса стороны сферического треугольника запишем навигационную функцию h:

 

(1.35)

Высота измеряется в плоскости вертикала светила, которая ориентирована по направлению азимута. Плоскость вертикала образует на поверхности модели Земли, т.е. сферы, большой круг, поэтому элементарное приращение высоты dh=dn, а в соответствии с формулой (1.4) g_h=1. На рис. 1.16 вертикал светила совпадает с меридианом светила.

 

 

 

Для подтверждения очевидной догадки воспользуемся формулой (1.35), в которой для упрощения будем считать, что l=t_гр, т.е. наблюдатель находится на меридиане светила, тогда:

(1.36)

И так, мы установили, что модуль градиента высоты светила g _h = 1, а t_h=A=180⁰, где А- азимут светила (по нашим условиям наблюдатель и светило находятся на одном меридиане).

1.10 Прямой аналитический расчет координат места судна

Для определения координат места судна на двумерной поверхности земного эллипсоида или шара необходимо измерить,как минимум, два навигационных параметра, и зная выражение навигационной функции, записать систему уравнений навигационных изолиний.

В качестве примера на судне можем измерить два навигационных параметра (расстояния) D_A и D_B до ориентиров A (x_A,y_A) и B(x_B,y_B). Имеем систему уравнений навигационных функций:

(1.37)

Если, например, D_A = 5, а D_B =10, то система уравнений навигационных изолиний запишется так:

(1.38)

Теперь необходимо решить систему (1.38) относительно неизвестных координат (x,y), которые и являются координатами места судна.

Прямое аналитическое решение таких задач имеет достаточно сложный вид даже для простых навигационных функций. Рассмотрим задачу определение места по двум пеленгам на плоскости.

Система уравнений запишется из (1.10), в соответствии с рис. 1.18 будет иметь вид:

(1.39)

 

где х₁,х₂, y₁, y₂ – координаты навигационных ориентиров.

Обозначив tg П ₁ через Т₁,а tg П ₂ через Т₁ ,х₀ =х, y₀ =y, запишем алгоритм решения системы:

 

a) Т₁(х₁–х₀)-y₁ = Т₂(х₁–х₀)–y₂;

b) х₀=(Т₂х₂-Т₁х₁+y₁–y₂)/(Т₂-Т₁);

c) y₀=(Т₁Т₂(х₂-х₁)+Т₂y₁–Т₁y₁)/(Т₂-Т₁);

d) пусть П ₁=30°, П ₂=82°, тогда обсервованные прямоугольные координаты рассчитаем так:

e) х₀ =(tg(82°)*3-tg(30°)*8+5-9)/(tg(82°)-tg(30°) =1.95 мили

f) y₀ =(tg(30°)*tg(82°)*(3-8)+(tg(82°) *5-(tg(30°)*9)/(tg(82°)-tg(30°) =1.50 мили.

 

Подобные решения существует и при определении места судна другими способами: по двум расстояниям, двум горизонтальным углам, двум высотам светил (задача Гаусса), и т.д.

Прямые аналитические методы расчета координат имеют ряд недостатков:

Практически все навигационные функции являются нелинейными, а поэтому решение таких систем уравнений неоднозначно. Неоднозначность решения может привести к опасной ситуации.

Методы решения не универсальны, что не дает единого подхода к синтезированию алгоритмов и программного обеспечения.

Как мы видели выше все навигационные функции на сфере описываются с помощью тригонометрических функций, которые, в силу своей периодичности, вносят дополнительную многозначность в расчет координат.

На практике прямой аналитический метод заменяют графоаналитическим подходом, т.е. навигационные изолинии прокладывают или заранее наносят на навигационной карте.

 

Линейные методы расчета координат места судна

Эта глава содержит описание методов обработки навигационной информации и оценки точности обсервации.

2.1 Линеаризация навигационных функций

Для устранения недостатков прямых аналитических методов расчета координат применяют процедуру линеаризации навигационных функций в окрестности некоторой точки, которая, как предполагают должна быть близка к обсервованной. В морской навигации- это счислимая точка (x_c,, y_c). Линеаризацию производят с помощью разложения навигационной функции в ряд Тейлора с сохранением только первых членов разложения. Геометрически, это замена графика функции в счислимой точке (навигационной изолинии) касательной к ней. Эта касательная называется линией положения. Так как в измерениях всегда присутствуют погрешности,то измеренный НП никогда не совпадет со НП в счислимой точке (счислимый НП), а поэтому линия положения из-за погрешности измерения сместится параллельно самой себе в сторону измеренной навигационного параметра.

Другими словами, разность между обсервованным U_о (измеренным) и счислимым U_c навигационными параметрами может быть элементарно мала и представлена в виде дифференциала навигационной функции U=f(x,y), вычисленного для некоторой малой окрестности счислимой точки.

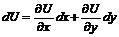(2.1)

На практике дифференциалы dU,dx,dy заменяют конечными приращениями и формула (2.1) принимает вид:

(2.2)

В навигации же принято записывать линейное уравнение (2.2) в виде:

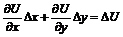(2.3)

или

(2.3a)

В (2.3) и (2.3a) D U = U_о - U_c, D x = x_о - x_c, D y = y_о - y_c – разности обсервованных и счислимых НП и координат.

Для графического решения задач определения места судна уравнения типа (2.3) используются в навигации в нормированном виде (2.4), который получается при делении (2.3) на модуль градиента навигационной функции:

(2.4)

Здесь выражения (2.3), как и (2.4) описывают линию положения, а D n - перенос линии положения от счислимой точки по направлению вектора- градиента, т.е. по нормали к изолинии. Правая часть (2.4) полностью согласуется с выражением (1.4).

В соответствии с нашими рассуждениями дадим определение линии положения:

 

 

Уравнение (2.4) с учетом формул параграфа 1.1 может быть переписано так:

(2.5)

Для навигационной функции расстояния, иллюстрация линии положения представлена на рис. 2.1

 

 

 

2.2 Аналитический вариант расчета координат места судна по двум линиям положения

 

Для определения места судна достаточно измерение двух навигационных параметров, так как поверхность на которой ищутся обсервованные координаты двухмерная (положение точки определяется двумя координатами).

Алгоритм расчета таков:

a. В момент времени t измеряются два навигационных параметра U_о1 и U_о2.

b. На этот же момент времени снимаются счислимые координаты x_с,y_с и на них рассчитываются счислимые навигационные параметры U_с1 и U_с2.

c.