КГТУ им.Туполева (АФ)
Кафедра ЕНД и ИТ
Дисциплина: Высшая математика
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
КОНТРОЛЬНЫХ РАБОТ №1 И №2.
Контрольная работа №1.
Темы: Элементы линейной алгебры и аналитической геометрии.
Задание №1. Тема: Вычисление определителей.
Определителем второго порядка называется число
 .
.
Определителем третьего порядка называется число
 .
.
Этот способ вычисления носит название «метод треугольников Саррюса» и подчиняется следующему правилу: первые три слагаемых со знаком (+) - это произведения элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали (рис.1а). Следующие три слагаемых со знаком (-) - это произведения элементов на побочной диагонали и элементов, стоящих в вершинах треугольников, с основаниями, параллельными побочной диагонали (рис.1б).
 |  |














рис.1а рис.1б
Определитель можно разложить по элементам любой строки или столбца. Формулы для вычисления определителей будут выглядеть следующим образом:
 - разложение определителя по строкам;
- разложение определителя по строкам;
 - разложение определителя по столбцам.
- разложение определителя по столбцам.
Здесь  ×
×  - алгебраические дополнения соответствующих элементов определителя,
- алгебраические дополнения соответствующих элементов определителя,  - миноры элементов определителя (минор - определитель, полученный вычеркиванием из данного определителя i -ойстроки и j -гостолбца).
- миноры элементов определителя (минор - определитель, полученный вычеркиванием из данного определителя i -ойстроки и j -гостолбца).
Так, например, разложение определителя по первой строке имеет вид:
 ×
× 
 (1)
(1)
На практике удобно пользоваться схемами знаков алгебраических дополнений:
 - для определителя третьего порядка;
- для определителя третьего порядка;
 - для определителя четвертого порядка.
- для определителя четвертого порядка.
При вычислении определителей удобно пользоваться следующими их свойствами:
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (транспонирование).
2. При перестановке двух строк (или столбцов), определитель изменит знак на противоположный, сохраняя абсолютную величину.
3. Определитель, имеющий две линейно зависимые (пропорциональные) строки (столбца) равен нулю. В частности, определитель, имеющий две одинаковые строки (столбца) равен нулю.
4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя. В частности, определитель, имеющий нулевую строку (столбец), равен нулю.
5. Значение определителя не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, отличное от нуля.
6. Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
7. Определитель треугольной матрицы равен произведению элементов, расположенных на главной диагонали.
Пример 1. Найти значения определителей:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 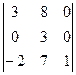 ; д)
; д)  .
.
Решение:
а) имеется нулевая строка; согласно свойству 4 определитель равен 0;
б) и в) – определители треугольного вида; согласно свойству 7 значения равны соответственно -32 и -80;
г) разложим определитель по элементам третьего столбца:
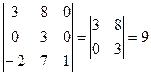 ;
;
д) первая и четвертая строки определителя пропорциональны; согласно свойству 3, значение его равно 0.
Пример 2. Вычислить определитель  .
.
Решение: Разложим определитель по элементам второй строки:
 .
.
Пример 3. Вычислить определитель  .
.
Решение. Разложим определитель по первой строке:
 =
=








 1×
1×  -2×
-2×  + 0×
+ 0×  - 1×
- 1×  =
=
= 3×  + 2×
+ 2×  - 2×
- 2×  - 4×
- 4×  - 1×
- 1×  + 3×
+ 3×  = -2.
= -2.
Пример 4. Вычислить определитель  .
.
Решение. Понизим порядок определителя. В первом столбце получим три (кроме единицы во второй строке) нулевых элемента, для чего произведем следующие действия:
- умножим элементы второй строки на число (-3) и сложим с элементами первой строки;
- умножим элементы второй строки на 2 и сложим с элементами третьей строки;
- из элементов четвертой строки вычтем элементы второй строки.
Тогда исходный определитель преобразуется к виду:
 .
.
Разложим этот определитель по элементам первого столбца:
 .
.
Прибавляем к элементам первой строки элементы третьей строки и, вычитая из элементов второй строки элементы третьей строки, получим
 .
.
Разложим полученный определитель по элементам первого столбца:
 .
.
Задание № 2. Тема: Действия над матрицами.
1) Умножение матрицы на число.
Произведением матрицы  на число
на число  называется матрица В, определяемая равенством
называется матрица В, определяемая равенством  . Отсюда следует, что общий множитель всех элементов матрицы можно вынести за знак матрицы.
. Отсюда следует, что общий множитель всех элементов матрицы можно вынести за знак матрицы.
2) Сложение и вычитание матриц (только для матриц одинаковой размерности). Так, для матриц  и
и  имеет место равенство
имеет место равенство  ,
, 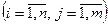 .
.
3) Произведение матриц.
Произведением матрицы  размерности
размерности  на матрицу
на матрицу  размерности
размерности  называется матрица
называется матрица  размерности
размерности  , определяемая равенством
, определяемая равенством 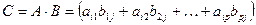 ,
, 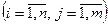 .
.
Т.е., элемент матрицы произведения, стоящий в i -ой строке и j- ом столбце, равен сумме произведений соответствующих элементов i -ой строки матрицы  и j- го столбца матрицы
и j- го столбца матрицы  . Таким образом, произведение матриц осуществляется по принципу "строка на столбец".
. Таким образом, произведение матриц осуществляется по принципу "строка на столбец".
Произведение матриц некоммутативно, т.е.  .
.
Исключение:  (для матриц одинаковой размерности).
(для матриц одинаковой размерности).
Пример 1. Перемножить матрицы  и
и  .
.
Решение. Произведение данных матриц возможно, так как число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  . Чтобы получить элемент
. Чтобы получить элемент  матрицы произведения, умножим первую строку матрицы
матрицы произведения, умножим первую строку матрицы  на первый столбец матрицы
на первый столбец матрицы  :
:
 .
.
Элемент  получится умножением первой строки матрицы
получится умножением первой строки матрицы  на второй столбец матрицы
на второй столбец матрицы  :
:
 .
.
Элемент  - умножением первой строки матрицы
- умножением первой строки матрицы  на третий столбец матрицы
на третий столбец матрицы  :
:
 .
.
Элемент  - умножением второй строки матрицы
- умножением второй строки матрицы  на первый столбец матрицы
на первый столбец матрицы  :
:
 .
.
Далее, умножая вторую строку матрицы  на второй столбец матрицы
на второй столбец матрицы  , получим
, получим  ; умножая вторую строку матрицы
; умножая вторую строку матрицы  на третий столбец матрицы
на третий столбец матрицы  , получим
, получим  . Результат
. Результат
 .
. 
3) Возведение матрицы в степень.
Целой положительной степенью  квадратной матрицы
квадратной матрицы  называется произведение
называется произведение  матриц, равных
матриц, равных  , т.е.
, т.е. 
4) Транспонирование.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной.
Обозначение  или
или  .
.
Пример 2. Транспонировать матрицу  .
.
Решение.  .
.
Задание 3. Тема: Обратная матрица.
Для невырожденной квадратной матрицы  любого порядка можно найти так называемую обратную матрицу
любого порядка можно найти так называемую обратную матрицу  , удовлетворяющую условию
, удовлетворяющую условию
 , (2)
, (2)
где  – единичная матрица того же порядка, что и матрица
– единичная матрица того же порядка, что и матрица  .
.
Алгоритм вычисления обратной матрицы:
1. Найти определитель матрицы. Если 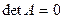 , то матрица
, то матрица  - вырожденная и обратной матрицы для нее не существует. Если
- вырожденная и обратной матрицы для нее не существует. Если  , то матрица
, то матрица  - невырожденная и обратная матрица существует.
- невырожденная и обратная матрица существует.
2. Найти матрицу алгебраических дополнений  .
.
3. Транспонировать  , т.е. найти
, т.е. найти  .
.
4. Найти обратную матрицу по формуле
 . (3)
. (3)
5. Проверка: согласно определению (2)  .
.
Пример 1. Дано  . Найти
. Найти  .
.
Решение. Найдем  , разложив его по элементам первой строки:
, разложив его по элементам первой строки:
 .
.
Матрица невырожденная, следовательно, обратная матрица существует.
Найдем алгебраические дополнения.
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
Таким образом, матрица алгебраических дополнений имеет вид:
 ,
, 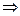
 .
.
Согласно формуле (3) находим обратную матрицу
 =
=  .
.
Проверка: согласно условию (*) имеем:
 .
.
Получилась единичная матрица, значит обратная матрица найдена верно.
Задание 4. Тема: Решение систем линейных алгебраических уравнений.
Рассмотрим систему линейных алгебраических уравнений (СЛАУ):
 . (4)
. (4)
Числа  , где
, где  ,
,  образуют матрицу системы:
образуют матрицу системы:
 .
.
Числа  , (
, ( ) образуют столбец свободных членов
) образуют столбец свободных членов  .
.
 - столбец неизвестных.
- столбец неизвестных.
Решением СЛАУ является всякий набор значений неизвестных  , удовлетворяющих системе, т.е. значения
, удовлетворяющих системе, т.е. значения  , при подстановке которых все уравнения системы обращаются в тождества.
, при подстановке которых все уравнения системы обращаются в тождества.
Матричный метод решения СЛАУ.
Нахождение решения СЛАУ по формуле
 (5)
(5)
называют матричным способом решения СЛАУ.
Пример 1. Решить матричным способом СЛАУ  .
.
Решение. Здесь матрица системы  , причем
, причем  .
.
Находим обратную матрицу  .
.
Делаем проверку: 
 ·
· 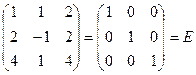 .
.
Тогда согласно формуле (5)  ×
×  =
=  .
.
Таким образом, решение СЛАУ:  .
.
Формулы Крамера.
При  СЛАУ совместна, причем, она имеет единственное решение, которое может быть найдено по формулам Крамера
СЛАУ совместна, причем, она имеет единственное решение, которое может быть найдено по формулам Крамера
 , (6)
, (6)
где  - определитель матрицы
- определитель матрицы  системы, а определители
системы, а определители  получены из определителя
получены из определителя  заменой столбца при каждой переменной столбцом свободных членов:
заменой столбца при каждой переменной столбцом свободных членов:
 .
.
Решение СЛАУ по формулам (6) называют решением методом Крамера.
Если  и при этом
и при этом  , то СЛАУ может иметь бесконечно много решений (при условии эквивалентности каких-либо уравнений системы), либо вообще не иметь решений.
, то СЛАУ может иметь бесконечно много решений (при условии эквивалентности каких-либо уравнений системы), либо вообще не иметь решений.
Если  и при этом какой-либо из определителей
и при этом какой-либо из определителей  отличен от нуля, то система не имеет решений (несовместна).
отличен от нуля, то система не имеет решений (несовместна).
Пример 2. Решить матричным способом СЛАУ  .
.
Решение.
 ,
,  ,
,  ,
,  .
.
Таким образом,  .
.
Метод Гаусса
Это метод последовательного исключения неизвестных. Осуществляется он в два этапа:
1) С помощью элементарных преобразований над система приводится к ступенчатому (треугольному) виду; при этом, последнее уравнение системы имеет одну неизвестную;
2) Последовательно находятся неизвестные из уравнений системы.
Рассмотрим решение СЛАУ методом Гауссана примере системы:
 .
.
Исключим  из всех уравнений кроме первого. Для этого произведем следующие действия:
из всех уравнений кроме первого. Для этого произведем следующие действия:
- умножим первое уравнение на (-4) и сложим его со вторым уравнением;
- умножим первое уравнение на 5 и сложим его с третьим уравнением.
Получим следующую систему:
 .
.
На втором шаге исключения первое уравнение переписывается без изменения. Другие два уравнения содержат две неизвестные  и
и  , и к ним можно применить ту же процедуру исключения. Для этого второе уравнение умножаем на 3 и складываем с третьим. Получаем систему
, и к ним можно применить ту же процедуру исключения. Для этого второе уравнение умножаем на 3 и складываем с третьим. Получаем систему
 .
.
Система приведена к треугольному виду.
Обратный ход: из третьего уравнения  ; подставляя это значение во второе уравнение, находим
; подставляя это значение во второе уравнение, находим  ; и, наконец, из первого уравнения
; и, наконец, из первого уравнения  .
.
Если в процессе решения СЛАУ методом Гаусса какое-либо уравнение принимает вид  , то СЛАУ имеет бесконечное множество решений, так как в этом случае в системе содержатся линейно зависимые уравнения. Если же возникнет уравнение
, то СЛАУ имеет бесконечное множество решений, так как в этом случае в системе содержатся линейно зависимые уравнения. Если же возникнет уравнение  , то система несовместна.
, то система несовместна.
Задание 5. Тема: Векторная алгебра.
Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора
, называется ортом вектора  и обозначается
и обозначается  .
.
Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых; обозначение  ||
||  , или с уточнением:
, или с уточнением:  для сонаправленных векторов (направленных в одну сторону) и
для сонаправленных векторов (направленных в одну сторону) и  для противоположно направленных векторов.
для противоположно направленных векторов.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Свободный вектор  (т.е. такой вектор, который без изменения длины и направления, может быть перенесен в любую точку пространства), заданный в координатном пространстве
(т.е. такой вектор, который без изменения длины и направления, может быть перенесен в любую точку пространства), заданный в координатном пространстве  , может быть представлен в виде
, может быть представлен в виде
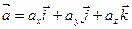
Такое представление вектора  называется его разложением по ортам. Здесь
называется его разложением по ортам. Здесь  - проекции вектора на соответствующие координатные оси (их называют координатами вектора
- проекции вектора на соответствующие координатные оси (их называют координатами вектора  );
);  - орты координатных осей (единичные векторы, направление каждого из которых совпадает с положительным направлением соответствующей оси, см. рис. 1).
- орты координатных осей (единичные векторы, направление каждого из которых совпадает с положительным направлением соответствующей оси, см. рис. 1).



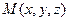



0 


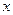
Рис. 1
Направление вектора  определяется углами
определяется углами  и
и  , образованными вектором с осями координат. Косинусы этих углов (направляющие косинусы) определяются равенствами:
, образованными вектором с осями координат. Косинусы этих углов (направляющие косинусы) определяются равенствами:
 ,
,  ,
,  , где
, где  - длина вектора
- длина вектора  .
.
Направляющие косинусы являются координатами орта 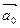 .
.
Направляющие косинусы связаны между собой соотношением
 .
.
Вектор  , начало которого находится в начале координат, а конец в точке
, начало которого находится в начале координат, а конец в точке 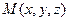 (рис.1) называют радиус-вектором точки М и обозначают
(рис.1) называют радиус-вектором точки М и обозначают  или просто
или просто  . Разложение вектора
. Разложение вектора  по ортам имеет вид:
по ортам имеет вид:  .
.
Вектор  , имеющий начало в точке
, имеющий начало в точке  и конец в точке
и конец в точке  имеет координаты
имеет координаты  . Длина этого вектора
. Длина этого вектора
 .
.
Произведения векторов.
1) Скалярным произведением векторов  и
и 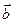 называется число, равное произведению длин этих векторов на косинус угла между ними
называется число, равное произведению длин этих векторов на косинус угла между ними
 , (1)
, (1)
где  (рис. 2).
(рис. 2).

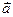

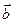
Рис. 2
Скалярное произведение обладает следующими свойствами:
·  . В частности,
. В частности,  ;
;
· Ненулевые векторы перпендикулярны, если  .
.
·  (переместительный закон);
(переместительный закон);
·  (распределительный закон).
(распределительный закон).
Если векторы  и
и 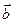 заданы в координатной форме:
заданы в координатной форме:  ,
,  ,то
,то
 .
.
Проекция вектора  на вектор
на вектор 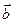 равна отношению скалярного произведения векторов
равна отношению скалярного произведения векторов  и
и 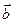 к длине вектора
к длине вектора 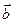 :
:
 . (2)
. (2)
2) Векторным произведением вектора  на вектор
на вектор 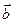 называется вектор
называется вектор  , длина и направление которого определяются следующим образом:
, длина и направление которого определяются следующим образом:
- вектор  перпендикулярен векторам
перпендикулярен векторам  и
и 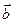 ;
;
- векторы  ,
, 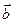 и
и  образуют правую тройку векторов (рис. 3);
образуют правую тройку векторов (рис. 3);
- длина вектора  равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах  и
и 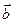 , т.е.
, т.е.
 , (3)
, (3)
где  .
.
Три некомпланарных вектора  ,
, 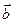 и
и  образуют правую тройку, если после приведения их к общему началу движение от вектора
образуют правую тройку, если после приведения их к общему началу движение от вектора  к вектору
к вектору  через вектор
через вектор 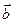 совершается против часовой стрелки.
совершается против часовой стрелки.


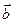


Рис. 3. Правая тройка векторов.
Основные свойства векторного произведения
1)  ;
;
2) 
3) если  , причем
, причем  и
и  , то
, то  ||
||  (векторы коллинеарны); верно и обратное утверждение. В частности
(векторы коллинеарны); верно и обратное утверждение. В частности  ;
;
4)  (следствие из (3));
(следствие из (3));
5)  (распределительный закон);
(распределительный закон);
Если  и
и  , то
, то

 , (4)
, (4)
Смешанное произведение.
Смешанным произведением векторов  ,
, 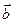 и
и  называется скалярное произведение вектора
называется скалярное произведение вектора  ´
´ 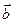 на вектор
на вектор  :
:
 . (5)
. (5)
Смешанное произведение – число, равное, по абсолютной величине, объему параллелепипеда, построенного на перемножаемых векторах (рис. 4)
 |

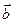

Рис. 4
Если  ,
,  ,
,  , то
, то

 , (6)
, (6)
причем вопрос о порядке сомножителей решается на основании свойств определителей третьего порядка, а именно:
- при перестановке любых двух сомножителей смешанное произведение изменит знак, т.е.
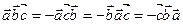 ;
;
- смешанное произведение не изменится, если переставлять перемножаемые вектора в круговом порядке:
 .
.
Свойства смешанного произведения
1) Смешанное произведение равно нулю, если:
а) хотя бы один из перемножаемых векторов равен нулю;
б) два из перемножаемых векторов коллинеарны;
в) три ненулевых вектора компланарны.
2) Смешанное произведение не изменится, если в нем поменять местами знаки векторного и скалярного умножения, т.е
( ´
´ 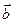 )×
)×  =
=  ×(
×(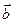 ´
´  ).
).
Пример 1. Найти площадь треугольника  , если известны координаты его вершин:
, если известны координаты его вершин:  .
.
Решение: По определению векторного произведения

Имеем 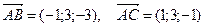 . Тогда
. Тогда
 .
.
Таким образом,  .
.
Пример 2. Образуют ли векторы  базис? Если да, то найти разложение вектора
базис? Если да, то найти разложение вектора  в этом базисе.
в этом базисе.
Решение. В пространстве любые три некомпланарные векторы образуют базис. Векторы  ,
, 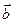 и
и  будут образовывать базис, если их смешанное произведение равно нулю. Проверим это.
будут образовывать базис, если их смешанное произведение равно нулю. Проверим это.
 .
.
Разложение вектора  в базисе
в базисе  ,
, 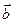 ,
,  имеет вид
имеет вид 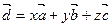 . Координаты
. Координаты  (коэффициенты разложения) вектора
(коэффициенты разложения) вектора  должны удовлетворять системе:
должны удовлетворять системе:
 ,
,
откуда имеем
 .
.
Следовательно, искомое разложение:
 .
.
Задание 6. Тема: Аналитическая геометрия в пространстве.
Плоскость в пространстве.
Каноническое уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  (рис. 1) имеет вид:
(рис. 1) имеет вид:
 (1)
(1)
Вектор  называется нормалью к плоскости.
называется нормалью к плоскости.


Рис. 1
Уравнение (1) можно привести к общему виду:
 , (2)
, (2)
где  .
.
Уравнение плоскости, проходящей через три заданные точки  ,
,  ,
,  имеет вид:
имеет вид:
 . (3)
. (3)
Угол между плоскостями  и
и  равен углу между нормалями к этим плоскостям. Косинус этого угла равен
равен углу между нормалями к этим плоскостям. Косинус этого угла равен
 . (4)
. (4)
Следует заметить, что под углом между плоскостями понимается один из двугранных углов, образованных этими плоскостями. Для нахождения острого угла следует взять модуль правой части равенства (4).
Расстояние  от точки
от точки  до плоскости
до плоскости  находится по формуле:
находится по формуле:
 . (5)
. (5)
Прямая в пространстве.
Канонические уравнения прямой, проходящей через точку  параллельно вектору
параллельно вектору  , имеют вид:
, имеют вид:
 . (6)
. (6)
Вектор  называется направляющим вектором прямой.
называется направляющим вектором прямой.
Уравнения прямой, проходящей через две точки  и
и  , имеют вид
, имеют вид
 . (7)
. (7)
Если каждое из отношений, входящих в уравнения (7), приравнять к некоторому параметру 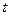 :
:
 ,
,
то получим параметрическое уравнениепрямой в пространстве:
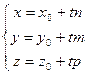 . (8)
. (8)
Косинус острого угла между прямыми  и
и  равен
равен
 .
.
Прямая и плоскость в пространстве.
Взаимное расположение прямой  и плоскости
и плоскости  в пространстве определяется взаимным расположением направляющего вектора
в пространстве определяется взаимным расположением направляющего вектора  прямой
прямой