Рассеивание случайной величины характеризует её разброс относительно точки математического ожидания. Так как разброс элементов спектра случайной величины происходит по обе стороны от центра рассеивания, то для его учета используют либо четные степени центральных моментов, либо абсолютные центральные моменты. Достаточно рассмотреть центральный момент второго порядка m2 и абсолютный центральный момент первого порядка t1. Первый из них называется дисперсией, а второй – средним отклонением. Изучим их подробнее.
Дисперсия случайной величины Х имеет несколько обозначений:
 – ДСВ;
– ДСВ;
D (X) =  = m2 = E (
= m2 = E ( 2) = (59)
2) = (59)
 – НСВ,
– НСВ,
Оператор дисперсии D обладает следующими свойствами:
1) D (C) = 0
2) D (CX) = C 2· D (X). (60)
3) D (C + X) = D (X)
Ситуация с доказательством свойств оператора дисперсии аналогична той, которая была отмечена для оператора математического ожидания. Остановимся на физическом смысле этих свойств.
Первое свойство говорит, что постоянная величина не имеет разброса. Комментарий не требуется.
При изменении масштаба по оси абсцисс (второе свойство), новое значение дисперсии получается из старого путем умножения последнего на величину квадрата масштабного коэффициента.
Третье свойство дисперсии заключается в том, что при переносе начала координат на величину C по оси абсцисс дисперсия случайной величины не меняется, так как центрирование компенсирует перенос.
Объединение этих свойств выражается реакцию оператора дисперсии на линейное преобразование случайной величины X:
D (C 1 + C 2 ∙ X) = C 22∙ D (X). (61)
Из определения дисперсии следует, что ее размерность равна квадрату размерности случайной величины, которую она характеризует. Это не всегда удобно для восприятия. Например, если сказать, что некоторое расстояние S = 567,89 м, а его дисперсия D (S) = 9∙10-4 м2, то сопоставление этих величин, имеющих отличающиеся размерности, не дает представления о точности измерений. Этот факт способствовал использованию дополнительно в качестве характеристики рассеивания другого показателя – стандарта.
Стандарт или среднее квадратическое отклонение (СКО) представляет собой положительное значение квадратного корня из дисперсии и характеризует разброс СВ относительно ее центра рассеивания в тех же единицах, в каких выражена и сама случайная величина:
 (62)
(62)
Свойства стандарта определяются свойствами дисперсии:
1) s C = 0
2) s CX = C ·s X (63)
3) s C + X = s X
Если теперь мы охарактеризуем ранее приведенное расстояние S=567,89 м стандартом sS =3*10-2 м, то наше представление о точности этого расстояния будет адекватным.
Среднее отклонение – это абсолютный центральный момент первого порядка для случайной величины Х, обозначаемый буквой ϑ X и вычисляемый по определению (58) при r = 1:
 – ДСВ;
– ДСВ;
ϑ X = τ1 = E (|  |)= (64)
|)= (64)
 – НСВ.
– НСВ.
Свойства среднего отклонения аналогичны свойствам стандарта (убедитесь в этом в качестве Упражнения 2.1):
1) ϑ X = 0
2) ϑ CX = | C |·ϑX (65)
3) ϑ C + X = ϑ X
2.2.6 Примеры одномерных распределений.
Рассмотрим законы распределений некоторых дискретных и непрерывных случайных величин, играющих важную роль в теории и практике.
Индикатор события.
Индикатор события IA представляет собой частный случай испытаний Бернулли. Это дискретная случайная величина, принимающая только два возможных значения 0 и 1 с вероятностями (1 – p) и p соответственно. Здесь p = P (A) – вероятность наступления события A, описанного на некотором пространстве W. Рассмотрим все введенные выше характеристики для этой случайной величины в качестве примера и с целью их использования при изучении более сложных законов.
Дано: X = IA = { x 1 = 0; x 2 = 1}; P (x 1) = P (Ā) = 1 – p = q; P (x 2) = P (A) = p.
Найти: 1) F (IA) –? 2) E (IA) –? 3) D (IA) –? 4) s I –?
Решение:
1)Функцию распределения разместим в расширенной таблице ряда распределения, как это предложено в (44):
| X = IA | - | ||
| P (X = IA) | q | p | - |
| F (IA) | q |
Числовые характеристики определим по формулам (51), (59) и (62):
2) E (IA) = 0∙ q + 1∙ p = p;
3) D (IA) =  =a2-
=a2-  = 02∙ q +12∙ p – p 2 = p ∙(1 – p) = pq;
= 02∙ q +12∙ p – p 2 = p ∙(1 – p) = pq;
4)  =
=  .
.
Индикатор событий используется при изучении повторных испытаний и решении других задач как вспомогательная случайная величина.
2.2.6.2 Равномерное распределение.
В качестве иллюстрации, поясняющей материал раздела 2.2 для непрерывных случайных величин, исследуем непрерывное равномерное распределение на некотором отрезке [ a; b ]. Распределение называется равномерным на отрезке, если его плотность вероятности постоянна на этом отрезке и равна нулю за его пределами. Представим изучение данного распределения в виде решения задачи.
Дано: f (x) = c,  [ a; b ]; f (x) = 0 вне этого отрезка.
[ a; b ]; f (x) = 0 вне этого отрезка.
Найти: 1) постоянную плотность распределения c –?, 2) F (x) –?, 3) E (X) –?, 4) Mo(X) –?, 5) Me(X) –?, 6) D (X) –?, 7) s X –?, 8) ϑ X –?, 9) P (x 1< X < x 2) –?
Решение: Выполнить самостоятельно в качестве Упражнения 2.2.
Ответы: 1) c = 1 / (b – a); 2) F (x) = (x – a) / (b – a); 3) E (X) = (a + b)/2;
4) Mo(X) – не определена; 5) Me(X) = E (X); 6) D (X) = (b – a)2 / 12;
7) s x = (b – a) /( ); 8) ϑ X = (b – a) / 4; 9) P (x 1< X < x 2) = (x 2 – x 1)/(b – a), когда ] x 1; x 2[
); 8) ϑ X = (b – a) / 4; 9) P (x 1< X < x 2) = (x 2 – x 1)/(b – a), когда ] x 1; x 2[ 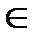 [ a; b ].
[ a; b ].
Графики плотности и функции равномерного распределения представлены на следующих рисунках (Рис.19 и 20).
f (x) F (x)
c
S =1 c =1/ 
0 a E (X) b X 0 a E (X) b X
Рис. 2.19 Плотность равномерного Рис. 2.20 Функция равномерного