Методика расчета транспортных задач
Целью работы является освоение методики решения транспортной задачи с применением компьютерных средств экономико-ста-тистических расчетов.
Компьютерные средства
| Операционная среда: | Windows 2000/XP |
| Программное средство: | Пакет программ для работ с электронными таблицами Microsoft Excel |
| Версия MS Excel; | Excel 97, Excel 2000 |
Теоретическая основа транспортной задачи
Транспортная задача представляет собой частный случай общей задачи линейного программирования и заключает в себе оптимальное распределение потока груза. В качестве критерия оптимальности принимают минимум затрат на перевозку груза.
Постановка задачи. В m пунктах отправления сосредоточен однородный груз в количестве А 1, А 2, …, Аm единиц. Необходимо этот продукт распределить по n потребителям в количестве В 1, В 2, …, Вn единиц, при условии получения минимальных затрат на перевозку.
Обозначим Хi,j – количество продукции, поставляемой i- м поставщиком j- му потребителю; Сi,j – стоимость перевозки из пункта i в пункт j.
Целевая функция  .
.
Ограничения:
Х 11 + Х 12 +…+ Х 1 m 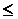 А 1 А 1
| Х 11 + Х 21 +…+ Хn 1 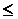 B 1 B 1
|
Х 21 + Х 22 +…+ Х 2m 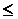 А 2 А 2
| Х 12 + Х 22 +…+ Хn 2 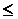 B 2 B 2
|
Х 31 + Х 32 +…+ Х 3m 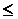 А 3 А 3
| Х 1 m + Х 2 m +…+ Хnm 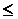 B 3 B 3
|
Общее условие транспортной задачи записывается в табличной форме (табл. 1).
Таблица 1

Для транспортных задач разработаны матричные методы решения, которые основаны на принципах:
- последовательного улучшения плана (потенциалов);
- последовательного сокращения невязок (дифференциальных рент, разрешаемых слагаемых).
Исходные данные
Исходные данные представлены в табл. 2.
Таблица 2

Пример решения транспортной задачи
методом дифференциальных рент
Исходные условия и отправной план представлены в табл. 3.
Таблица 3

Начальный план строим по методу наименьших значений.
В каждом столбце отыскиваем клетки с минимальными оценками. Заключаем их в квадрат.
Для В1 – это будет 1, для В2 – 5, В3 – 2 и В4 – 4. В правой строке клетки с наименьшими значениями стоимости перевозок проставляем планируемые поставки В1 = 70; В2 = 120; В3 = 80 и В4 = 0. В проведенном распределении в одних случаях (А3 и А4) не использованы полностью мощности заводов, а в других (В2, В3, В4) – не удовлетворен полностью спрос площадок.
Отметим, что распределение проведено с учетом получения минимума себестоимости, но исходные условия не удовлетворены.
Проверим по строкам, как использованы мощности поставщиков. Завод А1 поставляет 120 тыс. т на площадку В2, потребность которой составляет 130 тыс. т. Следовательно недостача (-) равна 10 тыс. т. Эту цифру записываем в правом последнем столбце. Завод А2 поставляет продукцию площадке В3-80, но потребность её равна 300 тыс. т, дефицит 220 тыс. т. Кроме того с этого завода железобетонные изделия должны поступать на площадку В4, но так как их больше нет, то поставка равна 0, следовательно суммарное недополучение потребителями В3 и В4 продукции завода А2 составит 220 тыс. т + 100 тыс. т = = 320 тыс. т. Указанную величину как недостачу записываем во второй строке последнего столбца. Мощность завода А3 использована всего на 70 тыс. т, избыток равен 180 тыс. т, а мощность А4 (150 тыс. т) не использована вовсе. Указанные величины также записываем в последнем столбце (строки 3 и 4), но со знаком “плюс”.
Если вся продукция завода распределена, а спрос полностью не удовлетворен, то поставщик называется недостаточным, а соответствующая строка “отрицательной”.
Если продукция завода распределена не полностью или совсем не распределена, то поставщик считается избыточным, строка – “положительной”.
Сумма недостающей продукции равна сумме избыточной, так как поставлено условие, что вся продукция должна быть распределена. Сумма излишней продукции называется “нераспределенным остатком”. При получении оптимального плана нераспределенный остаток должен быть равен нулю.
Задача заключается в том, чтобы постепенно распределить этот остаток, но, помня о том, что себестоимость должна быть минимальной. Это распределение, видимо, должно осуществляться путем постепенного включения в качестве поставщиков таких заводов, стоимость продукции которых была бы близкой к минимальной.
Для этого определим в столбце наименьшую разность между минимальной себестоимость и ближайшим к ней показателем, расположенным в положительной строке. При этом в столбцах матрицы, где имеется ходя бы один квадрат в одной из положительных строк (В1), такая разность не определяется. Так, в столбце В2 минимальная себестоимость равна 5, ближайшая к ней себестоимость в положительной строке равна 7, разность между А4В2 и А1В2: 7 - 5 = 2. В столбце В3 минимальная себестоимость равна 2, ближайшая к ней себестоимость в положительной строке равна 3, разность: 3 – 2 = 1. В столбце В4: 12 – 4 = 8.
Выбираем из полученных величин (2; 1; 8) наименьшую (1), называемую “промежуточной рентой”, и составим таблицу (табл. 4), в которую без изменений перепишем показатели стоимости по положительным строкам (А3 и А4), а показатели по отрицательным – получим путем прибавления к ним промежуточной ренты, в данном случае 1.
Таблица 4

Находим строки (столбцы), в которых имеется один квадрат (А1). Записываем в эти клетки объемы поставки, которые поставщики должны потребителям (в нашем случае – В2). После этого просматриваем столбцы (строки), среди них опять находим такие, где в квадрате только одна поставка – столбцы В1 и В4). В эти клетки (3.1 и 2.4) запишем поставки, равные соответственно 70 (потребителю В1) и 80 (потребителю В4). Потом снова просмотрим строки. Теперь в строке А2 остался только один квадрат, так как клетка с квадратом 3.3 уже использована, помещаем в клетку 2.3 – 0 единиц, так как у поставщика А2 взят груз в 80 единиц и направляем потребителю В4, и по строке А3 груз в 180 единиц и направляем потребителю В3 (остальные 70, взятые ранее у этого поставщика – для потребителя В1).
В результате получаем второй вариант распределения.
Величина нераспределенного остатка уменьшилась, следовательно второй вариант плана ближе к оптимальному.
Нераспределенный остаток должен, как правило, уменьшится на каждой последующей итерации. В отдельных случаях величина нераспределенного остатка может остаться на том же уровне, но при этом одна из положительных строк становится отрицательной. Увеличение нераспределенного остатка свидетельствует об ошибке.
Правило определения знака у нуля
По строке А3 вся продукция распределена и результат равен нулю. Если строка, нераспределенный остаток в которой равен нулю, связана квадратом с отрицательной строкой, т. е. часть продукции данному потребителю (В3) идет от “недостаточного” поставщика (А2), а А2 – отрицательная строка, то рассматриваемая строка А3 – отрицательная, а если строка связана с положительной, то она положительна.
Если строка, нераспределенный остаток в которой равен нулю, связана квадратом с отрицательной строкой, в которой записана нулевая поставка, или с несколькими строками, имеющие разные знаки, то для определения знака нулевой строки объем производства поставщика условно увеличивается (например на единицу) и заново производится распределение. Если при этом количество продукции, получаемой всеми потребителями, не изменится, то поставщик является избыточным и знак у нуля положительный, а если указанное количество увеличилось, то поставщик “недостаточен”, и строка отрицательна.
Проделав указанным способом еще три итерации в рассматриваемой задаче, получим оптимальный план распределения грузов (табл. 5, 6, 7 и 8).
Таблица 5

Таблица 6

Таблица 7
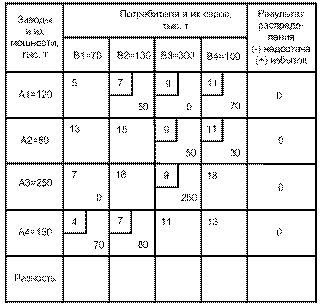
Таблица 8

Себестоимость перевозок по полученному плану составляет:
Сmin=50´5+50´7+20´9080´4+250´3+70´4+80´7 = 2 690 тыс. руб.
Оптимальный план должен удовлетворят следующим условиям:
- число заполненных клеток должно быть равно m + n – 1при невырожденной задаче;
- нераспределенный остаток должен быть равен нулю.
И то, и другое в последнем варианте плана удовлетворено, следовательно план оптимален.
Пример решения транспортной задачи
методом Северо-Западного угла
Распределяем продукцию от поставщиков к потребителям, начиная с Северо-Западного угла по диагонали (табл. 9).
Таблица 9

Проверяем условие m + n – 1 = Кз,
где m – количество потребителей;
n – количество поставщиков;
Кз – количество заполненных клеток.
4 + 4 – 1 = 7
Кз = 6
Заданное условие не выполняется, поэтому в любой клетке проставляем нулевую поставку.
Находим коэффициенты u и ν, выполняя условие:
u + ν – ci = 0, через загруженную ячейку;
u = ci – ν;
ν = ci – u.
Проверяем незагруженные клетки по формуле
u + ν = c
| (1;3) = 3 | (3;1) = – 5 |
| (1;4) = 3 | (3;2) = – 12 |
| (2;1) = 0 | (3;4) = – 7 |
| (2;3) =11 | (4;2) = – 1 |
| (2;4) = 11 – max |
Если все полученные значения отрицательны или равны нулю, то матрица оптимальна, и тогда рассчитывается себестоимость.
Если же матрица не оптимальна, то выбираем клетку с максимальноположительным значением и обозначаем её точкой. Из отмеченной точки строим n- угольник,вершины которого лежат на загруженных клетках. Переписываем n- угольник,расставляя знаки и поставки на вершинах, начиная с незагруженной вершины, чередуем плюс с минусом (рис. 1, 2, 3, 4).
Выбираем из минусов вершину, минимальную по модулю, и прибавляем модуль этого числа по всем вершинам, учитывая знаки. Строим следующую таблицу распределения с новыми поставками (табл. 10, 11, 12, 13).

Рис 1. Многоугольник с поставками
Таблица 10

4 + 4 – 1 = 6
6 ≠ 7
| (1;1) = – 11 | (3;1) = – 5 |
| (1;3) = – 8 | (3;2) = – 1 |
| (1;4) = – 8 | (3;4) = – 7 |
| (2;1) = – 11 | (4;2) = 10 – max |
| (2;3) = 0 |

Рис. 2. Многоугольник с поставками
Таблица 11

7 = 7
| (1;1) = – 5 | (2;3) = 0 |
| (1;3) = 2 – max | (3;1) = – 5 |
| (1;4) = 2 | (3;2) = – 11 |
| (2;1) = – 11 | (3;4) = – 7 |
| (2;2) = – 10 |

Рис. 3. Многоугольник с поставками
Таблица 12

7 = 7
| (1;1) = – 1 | (3;1) = – 3 |
| (1;4) = 2 | (3;2) = – 9 |
| (2;1) = – 11 | (3;4) = – 5 |
| (2;2) = – 10 | (4;3) = – 2 |
| (2;3) = – 2 |

Рис. 4. Многоугольник с поставками
Таблица 13

Решение транспортной задачи
в среде MS Excel
Перед началом работы, нужно настроить безопасность макросов. Это необходимо для корректной работы программы. Для этого следует выполнить следующие действия: выбрать из пункта меню Сервис/Макрос/Безопасность… и установить средний или низкий уровень безопасности (рис. 5). Если вы не уверены в используемых программой макросах, то понижать уровень безопасности не рекомендуется, потому что некоторые макросы содержат вирусы. Впрочем, для проверки программы на вирусы, необходимо использовать имеющиеся на вашем компьютере антивирусные программы (Dr Web, Kaspersky Anti-Virus).

Рис. 5. Настройка уровня безопасности макросов
Для использования программы, также необходимо произвести установку надстройки ”Поиск решения”. Для этого следует выполнить следующее действие: из пункта меню выбрать Сервис/Надстройки, в открывшемся окне отметить галочкой “Поиск решения” и нажать ОК (рис. 6).

Рис. 6. Установка надстройки ”Поиск решения”
Для решения транспортной задачи необходимо создать таблицу, показанную на рис. 7.

Рис. 7. Исходная таблица
Значения ячеек по столбцу В с четвертой по седьмую строку определяются суммированием данных ячеек соответствующих строк, начиная со столбца С до столбца F.
Например, значение ячейки B4 = СУММ(C4:F4).
Значения ячеек по 8 строке и столбцам от С до F определяются суммированием данных ячеек соответствующих столбцов с 4 по 8 строки.
Например, значение ячейки С8 = СУММ(C4:C7).
Теперь, используя исходные данные, введем на этом же листе требуемые объемы поставок и расстояния между складами и пунктами доставки (рис. 8).

Рис. 8. Таблица с исходными данными
В строке 14 по столбцам C-F определим грузооборот по каждому пункту доставки. К примеру для 1 пункта (ячейка С14) рассчитывается с помощью формулы
С16 = С4С10 + С5С11 + С6С12 + С7С13,
либо можно использовать функцию СУММПРОИЗВ:
С16 = СУММПРОИЗВ(C4:C7;C10:C13) (рис. 9).

Рис. 9. Определение грузооборота
В ячейке В14 по формуле = СУММ(С14:F14) вычисляется общий объем грузооборота.
Для решения поставленной задачи воспользуемся процедурой Поиск решения, которая находится в меню Сервис.
После выбора данной команды появится диалоговое окно (рис. 10).

Рис. 10. Диалоговое окно Поиск решения
Поскольку в качестве критерия оптимизации выбрана минимизация грузооборота, в поле Установить целевую ячейку введите ссылку на ячейку, содержащую формулу расчета общего объема грузооборота. В нашем случае – это ячейка $B$14. Чтобы минимизировать значение конечной ячейки путем изменения значений влияющих ячеек (влияющими, в данном случае это и изменяемые ячейки, являются ячейки, которые предназначены для хранения значений искомых неизвестных), переключатель установите в положение минимальному значению.
В поле Изменяя ячейки введите ссылки на изменяемые ячейки, разделяя их запятыми; либо, если ячейки находятся рядом, указывая первую и последнюю ячейку, разделяя их двоеточием ($С$4:$F$7). Это означает, что для достижения минимального грузооборота перевозок будут меняться значения в ячейках с С4 по F7, т. е. будет изменяться количество груза, перевезенного по конкретному маршруту.
В группе полей Ограничения нажмите кнопку Добавить. Появится диалоговое окно Добавление ограничения (рис. 11).

Рис. 11. Диалоговое окно Добавление ограничения
Следует ввести левую часть ограничения в левое поле, выбрать знак условия, накладываемого на значение и ввести правую часть ограничения. После ввода одного ограничения следует нажать кнопку Добавить и ввести следующее. По окончании ввода всех ограничений нажмите на кнопку ОК. В диалоговом окне появятся строки введенных ограничений (рис. 12).

Рис. 12. Поиск решения с указанными ограничениями
Для изменения и удаления ограничений в списке Ограничения диалогового окна Поиск решения укажите ограничение, которое требуется изменить или удалить. Выберите команду Изменить и внесите изменения, либо нажмите кнопку Удалить.
Первое условие $B$4:$B$7<=$B$10:$B$13. Оно означает, что значение в ячейке В4 должно быть меньше или равно значению в В10, в В5 меньше или равно, чем в В11, и так далее до В7 и В13.
В ячейках с В4 по В7 на листе находятся объемы поставок с конкретных складов. В ячейках с В10 по В13 – запасы на этих же складах. Так как невозможно вывести со склада больше, чем на нем есть, первое значение должно быть не больше второго.
Второе условие $С$4:$F$7>=0. Оно означает, что объем перевозок не может быть отрицательным. Грузопоток имеет только одно направление – от складов к пунктам доставки удобрений.
Последнее условие $С$8:$F$8>=$C$9:$F$9. Оно означает, что значения в ячейках восьмой строки должны быть больше или равны значениям в ячейках девятой строки, т. е. запросы пунктов доставки должны быть выполнены полностью.
Введенные условия должны позволить найти наиболее оптимальный вариант решения задачи. Нажмите кнопку Выполнить для подбора решения.
После нахождения решения появляется диалог Результаты поиска решения (рис. 13).

Рис.13. Диалоговое окно Результаты поиска решения
Нажав кнопку ОК, вы занесете вариант решения на рабочий лист (рис. 14).

Рис. 14. Результаты решения транспортной задачи
Таким образом, решение транспортной задачи позволяет выявить оптимальные маршруты перевозки грузов и минимизировать логические затраты.
Варианты заданий
| №вар | ||||||||||||||||||||||||||||||
| Поставщики | А | |||||||||||||||||||||||||||||
| В | ||||||||||||||||||||||||||||||
| С | ||||||||||||||||||||||||||||||
| D | ||||||||||||||||||||||||||||||
| Потребители | ||||||||||||||||||||||||||||||
| Расстояние | А-1 | |||||||||||||||||||||||||||||
| А-2 | ||||||||||||||||||||||||||||||
| А-3 | ||||||||||||||||||||||||||||||
| А-4 | ||||||||||||||||||||||||||||||
| В-1 | ||||||||||||||||||||||||||||||
| В-2 | ||||||||||||||||||||||||||||||
| В-3 | ||||||||||||||||||||||||||||||
| В-4 | ||||||||||||||||||||||||||||||
| С-1 | ||||||||||||||||||||||||||||||
| С-2 | ||||||||||||||||||||||||||||||
| С-3 | ||||||||||||||||||||||||||||||
| С-4 | ||||||||||||||||||||||||||||||
| D-1 | ||||||||||||||||||||||||||||||
| D-2 | ||||||||||||||||||||||||||||||
| D-3 | ||||||||||||||||||||||||||||||
| D-4 |

Список литературы
1. Бауэрсокс Д. Дж., Клосс Д. Дж. Логистика: интегрированная цель поставок / Пер. с англ. – М.: Олимп-Бизнес, 2001.
2. Гаджинский А. М. Логистика: учебник для высших и средних специальных учебных заведений. – М.: ИВЦ “Маркетинг”, 2002.
3. Голиков Е. А. Маркетинг и логистика. - М. ИД “Дашков и К0”, 1999.
4. Гордон М. П., Карнаухов С. Б. Логистика товародвижения. –М.: Центр экономики и маркетинга, 1998.
5. Зубков Г. С. и др. Торговая логистика: учебное пособие. – Ростов н/Д: РИЦ ун-та, 1997.
6. Колобов А. А., Омельченко И. Н. Основы промышленной логистики: учебное пособие. – М: Изд-во МГТУ им. Н.Э. Баумана, 1998.
СОДЕРЖАНИЕ
Методика расчета транспортных задач 3
Компьютерные средства.......................................................................................... 3
Теоретическая основа транспортной задачи. 3
Исходные данные. 4
Пример решения транспортной задачи методом дифференциальных рент. 5
Правило определения знака у нуля. 8
Пример решения транспортной задачи методом
Северо-Западного угла. 11
Решение транспортной задачи в среде MS Excel.................................................... 17
Варианты заданий..................................................................................................... 24
Список литературы................................................................................................... 26