Арифметические операции над сходящимися последовательностями.

Числовая последовательность- функция натурального аргумента x_n=f(n).

1,1,1,1,1…1

1,1/2,1/3…1/N

1,-1,1,-1…(-1)ª

X_n,n∈N

Число А наз. пределом последовательности Х_n если для любого сколь угодно малого положит. числа >0 найдётся такой номер N(), что как только n>N() то имеет место неравенство | X_n – A | <

Число А есть предел последовательности Xn если для любого ε > 0 найдётся такой номер N, начиная с которого (при n>N) все члены последовательности будут заключены в ε-окрестности какой бы она узкой ни была. Вне этой окрестности может быть лишь конечное число членов этой последовательности.

Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.

Имеют место следующие арифметические свойства пределов вещественных последовательностей:

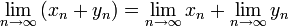
63.Расходящиеся последовательности. Бесконечно большие последовательности и их связь с бесконечно малыми последовательностями.

Последовательность расходящаяся. Числовая последовательность { x_n } называется расходящейся, если она не имеет конечного предела, т.е. если она либо имеет бесконечный предел, либо у нее вообще нет предела. В частности всякая неограниченная числовая последовательность расходится.

Если числовая последовательность содержит две или более двух подпоследовательностей, сходящихся к различным пределам, она расходится.

Функциональная последовательность (т.е. последовательность функций) { f_n(x) } называется расходящейся при данном значении х ₀ аргумента, если числовая последовательность { f_n(x ₀ ) } расходится.

В предыдущих статьях мы очень тесно рассматривали производную функции и предел функции в точке. Есть много способов подсчета пределов и мы их рассмотрим в следующей статье, но чтобы лучше понимать некоторые способы подсчета пределов сейчас рассмотрим понятия: бесконечно малые последовательности и бесконечно большие последовательности. Бесконечно малые последовательности Определение 1: Бесконечно малой последовательностью называется такая последовательность, что для сколь угодно малой окрестности нуля, вне окрестности будет только счетное число элементов последовательности, а в самой окрестности бесконечное число элементов последовательности. В дальнейшем нам мы будем применять свойства бесконечно малых последовательностей, поэтому перечислим несколько свойств и немного подробнее остановимся на каждом из них. Свойства бесконечно малых 1) Бесконечно малая последовательность является ограниченной последовательностью. Действительно, если бы она не была ограниченной, то вне достаточно малой окрестности нуля находилось бы бесконечное множество членов последовательности. 2) Любая конечная(конечное количество операций суммирования) сумма бесконечно малых последовательностей есть также бесконечно малая последовательность. 3) Произведение бесконечно малой последовательности на любую ограниченную последовательность или на любое конечное, отличное от нуля, число есть бесконечно малая последовательность. 4) Линейная комбинация счетного числа бесконечно малых последовательностей является бесконечно малой последовательностью. Бесконечно большие последовательности Также очень тесно с понятием последовательности связано понятие бесконечно большой последовательности. Определение 2: Бесконечно большой последовательностью называется такая последовательность, что для сколь угодно малой окрестности нуля, вне окрестности будет бесконечное число элементов последовательности, а в самой окрестности только счетное число элементов последовательности. Оба рассмотренных определения вводятся и для функций с различными способами задания. Данные определения мы рассмотрим в последующих статьях. 5) Если какая-то последовательность является бесконечно малой, то последовательность является бесконечно большой последовательностью.