Hахождение экстремумов функции двух переменных
Теоретическое введение
Пусть функция двух переменных z = f (x, y) = f (P) непрерывна в некоторой области G.
Функция двух переменных имеет в точке P 0 (x 0, y 0) области G максимум, если существует такая окрестность этой точки, что для всех точек P (x, y) этой окрестности, отличных от P 0, выполняется неравенство f (P 0) > f (P). Точка P 0 называется при этом точкой максимума функции f (x, y).
Функция двух переменных имеет в точке P 0 (x 0, y 0) области G минимум, если существует такая окрестность этой точки, что для всех точек P (x, y) этой окрестности, отличных от P 0, выполняется неравенство f (P 0) < f (P). При этом точка P 0 называется точкой минимума функции f (x, y).
Существует общее название для максимума и минимума – экстремум.
Необходимое условие существования экстремума. Если в точке P 0 (x 0, y 0) функция z = f (x, y) имеет экстремум и если в этой точке существуют частные производные первого порядка от функции z = f (x, y), то эти производные равны нулю, т.е.
| fx ' (x 0, y 0) = 0; f y' (x 0, y 0) = 0 | (1) |
Точки, в которых частные производные первого порядка функции z = f (x, y) равны нулю, называются стационарными. Точки, в которых частные производные первого порядка обращаются в нуль или не существуют, называются критическими этой функции. Точки экстремума функции следует искать среди её критических точек. Однако существуют критические точки, не являющиеся точками экстремума.
Достаточное условие существования экстремума. Пусть точка P 0(x 0, y 0) является стационарной для функции z = f (x, y) и пусть в этой точке существуют и непрерывны все частные производные второго порядка. Обозначим
A =  , B = , B =  , C = , C = 
| (2) |
и определитель второго порядка
Δ =  = AC – B 2 = AC – B 2
| (3) |
Если Δ > 0, то функция f (x, y) имеет в точке P 0 экстремум: минимум при A > 0 и максимум при A < 0.
Если Δ < 0, то в точке P 0 функция f (x, y) экстремума не имеет.
Если Δ = 0, то для заключения о характере стационарной точки требуется дополнительное исследование.
Пример. Исследовать на экстремум функцию z = x 3 + y 3 – 3 x – 12 y + 8.
Решение. Найдём частные производные первого порядка
z x' (x, y) = 3 x 2 – 3, z y' (x, y) = 3 y 2 – 12.
Найдём стационарные точки, решая систему уравнений (1)
 .
.
Заданная функция имеет четыре стационарные точки
M 1 (1; 2), M 2 (–1; –2), M 3 (1; –2), M 4 (–1; 2).
Найдём частные производные второго порядка (2)
 ,
,  ,
,  .
.
Определим знак Δ = AC – B 2 в каждой из стационарных точек
1) Точка M 1 (1; 2):
A = 6 x | x =1 = 6, C = 6 y | y =2 = 12, B = 0, Δ = 6 · 12 – 0 = 72 > 0.
Так как Δ > 0, то в точке M 1 существует экстремум. Поскольку A = 6 > 0, то M 1(1; 2) – точка минимума.
2) Точка M 2 (–1; –2):
A = 6 x | x = –1 = – 6, C = 6 y | y =-2 = –12, B = 0, Δ = (– 6) · (–12) = 72 > 0.
В точке M 2 также Δ > 0, т.е. существует экстремум. Однако здесь A = – 6 < 0, поэтому M 2(–1; –2) – точка максимума.
3) Точка M 3 (1; –2):
A = 6 x | x =1 = 6, C = 6 y | y = –2 = –12, B = 0, Δ = 6 · (–12) – 0 = –72 < 0.
Так как Δ < 0, то в точке M 3 экстремума нет.
4) Точка M 4 (–1; 2):
A = 6 x | x = –1 = – 6, C = 6 y | y = 2 = 12, B = 0, Δ = – 6 · 12 – 0 = –72 < 0.
Экстремума в точке M 4 нет.
Теперь вычислим значения заданной функции в точках экстремума M 1(1; 2) и M 2(–1; –2).
z max(M 2) = z max(–1; –2) = (–1)3 + (–2)3 – 3·(–1) – 12·(–2) + 8 = 24.
z min(M 1) = z min(1; 2) = 13 + 23 – 3 · 1 – 12 · 2 + 8 = –10.
Ответ: z max(M 2) = z max(–1; –2) = 24; z min(M 1) = z min(1; 2) = –10. В точках M 3 (1; –2) и M 4 (–1; 2) экстремумов нет.
Содержание типового расчета
Исследовать функцию двух переменных на экстремум:
z = Ax 3 + Bx 2 y + Cxy 2+ Dy 3 + Ex + Fy + G.
Пример выполнения типового расчета
Исследовать на экстремум функцию
z = – 5 x 3 – 4 x 2 y + xy 2 – 3 y 3 + 27 x + 36 y + 4.
Решение. Найдём частные производные первого порядка
zx' (x, y) = – 15 x 2 – 8 xy + y 2 + 27; zy' (x, y) = – 4 x 2 + 2 xy – 9 y 2 + 36.
Для нахождения стационарных точек нужно решить систему уравнений

Левые части уравнений системы являются однородными многочленами второго порядка относительно x и y (каждое слагаемое имеет второй порядок относительно x и y). Чтобы решить систему умножим каждое из уравнений на такое число, чтобы при сложении уравнений друг с другом свободный член обращался в нуль. Для этого первое уравнение умножим на – 4, а второе на 3.

Складывая уравнения, получим
48 x 2 + 38 xy – 31 y 2 = 0.
Замечаем, что y = 0 не является решением исходной системы уравнений, поэтому можно обе части полученного уравнения поделить на y 2 и ввести новое переменное 
 48 t 2 + 38 t – 31 = 0.
48 t 2 + 38 t – 31 = 0.
Полученное квадратное уравнение имеет корни 
 .
.
1) Пусть 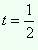 или
или  , y = 2 x. Подставим в первое уравнение системы, получим
, y = 2 x. Подставим в первое уравнение системы, получим
–15 x 2 – 16 x 2 + 4 x 2 = –27;  –27 x 2 = –27;
–27 x 2 = –27;  x 2 = 1;
x 2 = 1;  x = ±1.
x = ±1.
Получили две точки M 1(1; 2) и M 2(–1; –2).
2) Теперь рассмотрим 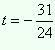 или
или  .
.
Снова подставляем в первое уравнение системы:

Умножим обе части уравнения на 312 и вынесем в левой части уравнения x 2 за скобки
(–15 · 312 + 8 · 24 · 31 + 242) x 2 = –27 · 312
Проведя расчёт, получим –7887 x 2 = –25947, x 2 ≈ 3,29, x ≈ ±1,81.
Учитывая, что  получаем ещё две стационарные точки M 3(1,81; –1,40), M 4(–1,81; 1,40).
получаем ещё две стационарные точки M 3(1,81; –1,40), M 4(–1,81; 1,40).
Найдём частные производные второго порядка



Определим знак Δ = AC – B 2 в каждой из стационарных точек
1) Точка M 1(1; 2).
A = (–30 x – 8 y)| M 1 = – 46; C = (2 x – 18 y)| M 1 = – 34;
B = (–8 x + 2 y)| M 1 = – 4; Δ = (– 46)·(–34) – (– 4)2 = 1548 > 0.
Так как Δ > 0, то в точке M 1 существует экстремум. Поскольку A = – 46 < 0, то M 1(1; 2) - точка максимума.
2) Точка M 2(–1; –2).
A = (–30 x – 8 y)| M 2 = 46; C = (2 x – 18 y)| M 2 = 34;
B = (–8 x + 2 y)| M 2 = 4; Δ = 46·34 – 42 = 1548 > 0.
В точке M 2 также Δ > 0, т.е. существует экстремум. Однако здесь A = 46 > 0, поэтому M 2(–1; –2) - точка минимума.
3) Точка M 3(1,81; –1,40).
A = (–30 x – 8 y)| M 3 = – 43,1; C = (2 x – 18 y)| M 3 = 28,82;
B = (–8 x + 2 y)| M 3 = 17,28; Δ = – 43,1·28,82 – 17,282 < 0.
Так как Δ < 0, то в точке M 3 экстремума нет.
4) Точка M 4(–1,81; 1,40).
A = (–30 x – 8 y)| M 4 = 43,1; C = (2 x – 18 y)| M 4 = – 28,82;
B = (–8 x + 2 y)| M 4 = – 17,28; Δ = 43,1·(–28,82) – (–17,28)2 < 0.
Экстремума в точке M 4 нет.
Вычислим значения исследуемой функции в точках экстремума M 1(1; 2) и M 2(–1; –2)
z max(M 1) = z max(1; 2) = 70;
z min(M 2) = z min(–1; –2) = – 62.
Ответ:
| № | x | y | экстремум | z |
| максимум | ||||
| –1 | –2 | минимум | –62 | |
| 1,81 | –1,40 | экстремума нет | – | |
| –1,81 | 1,40 | экстремума нет | – |
Оформление отчета
В отчете необходимо привести все проделанные выкладки. В ответе записать координаты всех найденных критических точек. Для каждой точки записать результат проведенного исследования: есть ли там экстремум или нет, если есть, то какой – максимум или минимум. Если в критической точке существует экстремум, необходимо вычислить значение функции в этой точке. Результаты исследования свести в таблицу, как показано в примере. В ответе все расчетные величины записать в десятичных дробях с тремя значащими цифрами.