Составила Федорова Е.А.
ОДОБРЕНЫ
Предметной (цикловой) комиссией экономики и информационных технологий
Председатель
_________________К.А. Кузьменко
Автор: Федорова Елена Анфимовна, преподаватель
Рецензенты: Горская Наталья Владимировна, преподаватель
В данном пособии рассмотрены базовые понятия интегрального исчисления: понятие первообразной функции, понятие неопределенного интеграла, основные свойства, формулы интегрирования, основные приемы интегрирования, приведены примеры, иллюстрирующие теоретический материал. Пособие дополнено упражнениями для самостоятельной работы, ответами к ним, приведены вопросы и образцы заданий для промежуточного контроля знаний. Предназначено для студентов, изучающих дисциплину «Элементы высшей математики» в средних профессиональных заведениях, обучающихся по очной, заочной, вечерней форме обучени, или имеющих свободное посещение занятий.
.
Содержание
Введение. 4
Требования к знаниям и умениям.. 4
Понятие неопределенного интеграла. 5
Основные свойства неопределенного интеграла. 6
Формулы интегрирования. 7
Выделение интегральной кривой по начальным условиям.. 9
Непосредственное интегрирование функций. 9
Метод подстановки. 11
Интегрирование по частям.. 12
Интегрирование рациональных функций. 13
Упражнения для решения. 15
Контрольные вопросы и примеры.. 18
Ответы и решения. 20
Литература. 36
Введение
Математический анализ дает ряд фундаментальных понятий, которыми оперирует экономика,— это функция, предел, производная, интеграл, дифференциальные уравнения.
Понятие неопределенного интеграла возникло в связи с необходимостью решать задачи, обратные задачам дифференцирования.
Действие, обратное дифференцированию, назвали интегрированием, т.о. интегрирование — это восстановление функций по данной производной.
Требования к знаниям и умениям
В результате изучения данной темы обучаемые должны знать:
- определения первообразной функции и неопределенного интеграла;
- простейшие свойства неопределенного интеграла;
- правила и формулы интегрирования.
В результате изучения данной темы обучаемые должны уметь:
- находить неопределенные интегралы непосредственно, с помощью подстановки, интегрированием по частям;
- решать простейшие задачи на приложения неопределенного интеграла.
Понятие неопределенного интеграла
Первообразной функцией для функции f (x) называется такая функция F (x), производная которой равна f (x).
По определению, если F (x) — первообразная функции f (x), то должно выполняться равенство:
(1)
Пример. Дано f (x) = 2 x, тогда 
, следовательно F (x) = x 2.
Но эта функция не единственная, другими являются x 2 + 2, x 2 — 3 и т.д., в общем виде x 2 + C, где C — const.
Теорема (основное свойство первообразной)
Если функция F (x) есть первообразная для функции f (x) на некотором интервале, то функция F (x) + с, где с — произвольная постоянная, также является первообразной для функции f (x) на данном интервале.
По условию F (x) — первообразная для функции f (x), следовательно .
Найдем производную 
Значит, по определению (1) F (x) + с также является первообразной для функции f (x).
Совокупность всех первообразных для функции f (x), x Î (a; b) называется неопределенным интегралом от функции f (x) и обозначается
f (x) d x = F (x) + с,где (2)
f (x) — подынтегральная функция,
f (x) d x — подынтегральное выражение,
x — переменная интегрирования.
Символ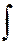 
— знак неопределенного интеграла.
F (x) — первообразная для функции f (x),
с — постоянная.
Интеграл называется неопределенным, т.к. результат неоднозначен.
Пример. Найти 
.
Т.к. 
, то 
является одной из первообразных для функции f (x) = x 5 и по формуле (2)
= 
, где с — const.
Слово «интеграл» впервые употребил Якоб Бернулли в 1890 г. Оно происходит от слова «Integer» — целый, восстанавливать.
Процесс нахождения первообразной функции называется интегрированием, а раздел математики, занимающейся вопросами, связанными с интегрированием, интегральным исчислением.
Таким образом, интегрирование — действие, обратное дифференцированию.
Пусть графиком некоторой первообразной y = F (x) является некоторая кривая, которую называют интегральной.
Тогда геометрически неопределенный интеграл представляет собой семейство интегральных кривых, каждая из которых получается из любой другой кривой параллельным переносом вдоль оси Oy.
Основные свойства неопределенного
интеграла
следуют из его определения.
1. Дифференциал неопределенного интеграла равен подынтегральному выражению
d 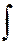f (x) dx = f (x) d x (3)
2. Производная неопределенного интеграла равна подынтегральной функции
(4)
3. Неопределенный интеграл от дифференциала функции равен самой этой функции, сложенной с произвольной постоянной
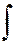d F (x) = F (x) + C (5)
а) 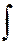d x = x + C;
б) 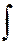d(x 4) = x 4 + C;
в) 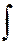d (sin 2y) = sin 2y + C.
4. Постоянный множитель можно выносить за знак неопределенного интеграла
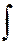R f (x) d x = R 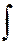f (x) d x, где R — const. (6)
5. Неопределенный интеграл от суммы непрерывных функций равен сумме интегралов от каждой из них
(f 1(x) + f 2(x) — f 3(x)) d x = f 1(x) d x + 
f 2(x) d x — f 3(x) d x. (7)
Формулы интегрирования
Т.к. интегрирование есть действие, обратное дифференцированию, то любая из нижеприведенных формул может быть доказана дифференцированием правой части (получим подынтегральную функцию).
Таблица интегралов
1) 
, n ¹ –1.
2) 
3) 
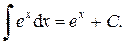
4) 
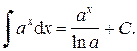
5) 
6) 
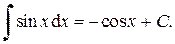
7) 
8) 
9) 
10) 
11) 
12) 
13) 
a ¹ 0.
14) 
15) 
16) 
17) 
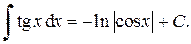
18) 
Пример. 
Для проверки результата надо:
а) найти производную или
б) найти дифференциал.
или
.
Выделение интегральной кривой
по начальным условиям
Геометрически неопределенный интеграл представляет собой семейство интегральных кривых, каждая из которых может быть получена из любой другой кривой параллельным переносом вдоль O y.
Семейство интегральных кривых определяется равенством
y = F (x) + C, (8)
где F (x) — первообразная для f (x), C — const.
Чтобы из множества всех интегральных кривых выделить одну определенную кривую должны быть заданы дополнительные (начальные) условия.
Начальными условиями обычно являются конкретные значения переменных x и y, по которым из равенства (8) находят значения постоянной C, а, следовательно, и одну вполне определенную интегральную кривую, удовлетворяющую заданным начальным условиям.
Пример. Найти уравнение кривой, проходящей через точку A(2;3), если угловой коэффициент касательной к кривой в каждой ее точке равен абсциссе этой точки.
Согласно геометрическому смыслу производной и условию задачи
k кас. = f ¢(x) = x.
Имеем f ¢(x) = x
.
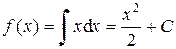Искомая функция
— уравнение семейства кривых
A (2; 3) принадлежит кривой, следовательно, координаты должны удовлетворять уравнению кривой.
Þ C = 1
— уравнение искомой кривой.