Привидение м-цы к ступенчатому виду.

Если

1. Если

2. Пусть Получим:

3, Прибавим ко 2й стр. первую, умноженную на (- ),к 3ей – 1ю, умноженную на (- ) и тд.

Получим A’’=

4. Забываем о первой строчке…Повторяем процедуру для м-цы из строк с 2й по m-ю…в конце получим

Такую матрицу называю ступенчатой(трепецивидной или треугольной.)

Вопрос 4. Определители 2-го и 3-го порядков. Определение определителя произвольного порядка.

(рассматриваем только квадратные матрицы!)

Определитель 2-го порядка

Пусть матрица А=

Определителем матрицы 2х2 называю число равное a*d-b*c

Обозначение: det A, det , |A|

Пример:

=1*4-2*3=-2

Определитель 3-го порядка

Пусть А=

det A= a₁₁*a₂₂*a₃₃+a₁₂*a₂₃*a₃₁+a₂₁*a₃₂*a₁₃ – a₁₃*a₂₂*a₃₁ – a₁₂*a₂₁*a₃₃ – a₂₃*a₃₂*a₁₁

«+» «-»

=1*-1*-1+2*2*1+1*0*-1 – 1*-1*1 – 1*2*-1 – 2*0*-1=8

Определение определителя порядка n.

Определителем матрицы порядка n называют числа равное

detA=Σ_{π принадлежит Sn} sgn π a_1π(n) a_2π(n)…a_nπ(n)

S_{n –} кол-во перестановок

Определитель – это сумма n! слагаемых, каждое с точностью до знака – это произведение элементов матрицы по одному из каждой строки и каждого столбца.

Для n=2 имеем 2 перестановки

1 2-> чётная

2 1 -> нечётная (1 перестановка)

detA=a₁₁*a₂₂ – a₁₂*a₂₁

для n=3 имеем 6 подстановок

123 – «+» 132 – «-» (1 инверсия) 213 - «-» 231 – «+» (2 инверсии) 312 – «+» 321 - «-» (3 инверсии)

Det A= a₁₁*a₂₂*a₃₃+a₁₂*a₂₃*a₃₁+a₂₁*a₃₂*a₁₃ – a₁₃*a₂₂*a₃₁ – a₁₂*a₂₁*a₃₃ – a₂₃*a₃₂*a₁₁

Вопрос 5. Свойства определителя

1.Если в матрице есть нулевая строка или столбец, то определитель равен нулю.

2.Если в матрице 2-е поменять местами, то определитель меняем знак.

Док-во:

А= 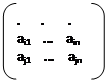A’ =

detA= …+sgn π a_1π(1)…a_nπ(n)^-1…

такое же разложение элемента встречается в разложении определения матрицы detA,

но оно будет соответствовать подстановке π’: π(1)…π(j)…π(i)…π(n)

Но π и π’ имеют разную чётность, т.е. sgn π= - sgn π’

detA’ = -detA

3.Если в матрице есть 2-е одинаковые строки, то определитель равен нулю.

4.Пусть одна строка матрицы является суммой 2-х строк

Тогда detA = detA’ + detA” Где А’= 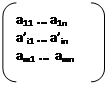A”=

Док-во:

detA=Σ*(a’_iπ(1)+ a”_iπ(1))=…= Σsgn π a_1π(1)*a’_iπ(1)+ a_1π(n)+ Σsgn π a_1π(1)*a”_iπ(1)+ a_1π(n)=detA’+detA”

если одну сторону матрицы умножить на λ принадлежит R, то определитель умножится на это число.

Док-во:

detA=Σ_π sgn π a_1π(1)…(λ* a_1π(1)* a_nπ(n))=…=λ*detA

если в строке матриц прибавить другую, умноженную на λ, то определитель не изменится.

λ принадлежит R

док-во:

= + λ =detA

detA ^t=detA

Следствие:

Все свойства с 1 по 6 справедливы для столбцов.

Вопрос 6. Разложение определителя по первой строке. Разложение определителя по произвольной строке(столбцу).

Определение:

Минор М_ij – это определитель матрицы получаемый из исходной вычёркиваемой i-той строки и

j-того столбца.

Теорема:

detA= a₁₁*M₁₁ – a₁₂*M₁₂+…+(-1)^n-1*a_1n*M_1n

Док-во:

detA= Σ_π sgn π a_1π(1)+…+a_nπ(n)=a₁₁Σ_π:π(1)=1 sgn π a_2π(2)…a_nπ(n)+a₁₂Σ _π:π(1)=2 sgn π a_2π(2)…a_nπ(n) +…+ a_1nΣ _π:π(1)=n sgn π a_2π(2)…a_nπ(n)

Если в перестановке убрать π(1) останется всё остальное π(1),π(2),…,π(n), то инверсий стало на

Π(1) - 1 меньше

а₁₁*М₁₁ – а₁₂*М₁₂ + …+ (-1)^n-1*a_1n*M_1n

Определение:

Алгебраическим дополнением элемента а_ij называются числа А_ij и равно (-1)^i-j*а_1n*M_1n,

Тогда определитель А=а₁₁*А₁₁+а₁₂*А₁₂+…+ a_1n*А_1n=Σ_к=1 а_1к*А_1к

Разложение определителя по произвольной строке

Теорема:

detА=а_i1*А_in+ …+ a_in*А_in=Σ_к=1 а_iк*А_iк

для любого i принадлежащего {1,…,n}

Док – во:

Используя перестановку строк поставим i-тую строку на 1-е место.

i-е меняем с (i-1)-й, затем с (i-2)-й и т.д.

за i-1 шагов => получим матрицу

А’=

detA’=(-1)^i-1*detA

detA’=a’₁₁*A’₁₁+a’_1n*A’_1n= a₁₁*A’₁₁+…+a_in*A’_1n= a_i1*(-1)¹⁺¹*M_i1+…+a_in*(-1)¹⁺ⁿ*M_in

detA=(-1)ⁱ⁺¹*detA’=(-1)ⁱ⁺¹*(a_i1*(-1)¹⁺¹*M_i1+…+a_in*(-1)¹⁺ⁿ*M_in)= a_i1*(-1)ⁱ⁺¹*M_i1+…+a_in*(-1)ⁱ⁺ⁿ* *M_in=a_i1*A_i1+…+a_in*A_in

Разложение по столбцу

detA=Σⁿ_k=1 a_kj*A_kj для любого j=1,…,n

Док-во: следует сразу же из того, что detA^t= detA

Вычисление определителя. С помощью элементарных преобразований можно привести матрицу к треугольному виду.

= a₁₁* = a₁₁*…*a₄₄

Замечания:

1.определитель единичной матрицы detE_n=1

det =λ₁*λ_n

2.определитель 2-х матриц –это произведение определителей detAB=detA*detB

3. разложение по чужой строке, если i≠j то определитель равен нулю.

Σⁿ_k=1 a_ik*A_jk=0

Σⁿ_k=0 a_ik*A_jk= 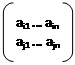=0

ВОПРОС №7Обратная матрица.

Определение: Матрица A’ называется равной обратной, если A A^-1=E.

Существование обратной матрицы:

а) Не у каждой матрицы есть обратная

Пусть det A=0. Если у матрицы A есть обратная A^-1, то A A^-1=E. Но det (A A^-1)=det A det A^-1=0

Значит, если det A=0, то у A нет обратной.

б) Покажем, что если det A 0, то обратная есть.

Пусть A =

Построим из алгебраических дополнений

A’ Ă = , т.к.

Тогда A^-1 = ^t

Построение обратной матрицы:

Построение обратной матрицы происходит аналогично пункту «б» существования матрицы.

ВОПРОС №8

МАТРИЧНЫЕ УРАВНЕНИЯ. ПРАВИЛО КРАМЕРА В ОБЩЕМ СЛУЧАЕ.

Пусть АХ=В - система линейных уравнений, причём А - невырожденная квадратная матрица.

Обозначим: ∆= detA( 0)

∆_i = определитель матрицы, полученный из матрицы А заменой i-го столбца на столбец В.

Тогда {x₁= , i = 1,2,.,n} является решением системы.

Покажем это:

Х=А^-1В= (А_ij)^t*B = = , но

A₁₁b₁+A₂₁b₂+...+A_n1b_n= =∆ и т.д. поэтому Х=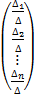

Пример:

;

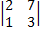∆ = = 13; ∆_х = = 44; ∆_y = = -1.

Решение: x = ; y =

ВОПРОС №9

АРИФМЕТИЧЕСКОЕ ЛИНЕЙНОЕ ПРОСТРАНСТВО. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ СТРОК.