Степенным рядом называется функциональный ряд вида
, (1)
где постоянные 
называются коэффициентами степенного ряда.n-ным членам степенного ряда называют членам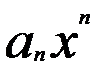 
, хотя он стоит в степенном ряде на n +1- месте.
Теорема Абеля. Если степенной ряд (1) сходится в точке 
, то он сходится абсолютна в интеграле (- 
) т.е. при всяком х, удовлетворяющем условию 
; если степенной ряд (1) расходится точки 
, то он расходится при всяком х, удовлетворяющим условию 
.
Из теоремы Абеля следует, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости заполняют некоторый интервал с центром в начале координат.
Для каждого степенного ряда, имеющего точки сходимости и расходимости, имеются положительное число R, что для всех х, удовлетворяющих условию 
, ряд сходится а для всех х, удовлетворяющих условию , ряд расходится. И это число Rназывается радиусом сходимости степенного ряда (1), а интервал (-R,R) –интервалом сходимости. При R= 
х ряд может сходится, может и расходится и для установления его сходимости.
Радиусы сходимости степенных рядов устанавливаются следующими способами. Составляются ряд из абсолютных величин членов степного ряда (1):
(2)
Для определения сходимости ряда с положительными членами (2) применяется признак Даламбера. Пусть существует предел
.
Тогда по признаку Даламбера ряд (2) сходится при 
, и расходится при 
. Следовательно, исходный ряд (1) сходится абсолютно, если 
, и расходится . Поэтому интервалом сходимости степенного ряда (1) будет (-R,R), где
. (3)
Радиус сходимости степенного ряда (1) определяется также с применением признаком Коши по формуле
(4)
Теорема 1. Степенные ряды можарируем на любом отрезке [-α, α], целиком лежащим внутри интервала сходимости (- R,R).
Теорема 2. Сумма можарируемого степного ряда S(x) есть функция, имеются внутри интервала сходимости (-R,R) производные любого порядка, каждая из которых есть сумма ряда, полученного по членном дифференцированием данного ряда соответствующее число ряд, при этом каждый ряд имеет один и тот же интервал сходимости (-R,R).
Теорема 3. Можарируемый степенной ряд (1) можно почленно интегрировать, если пределы интегрирования α, β лежат внутри интервала сходимости (-R,R), и интеграл от суммы S(x) ряда равен сумме интегралов о членов ряда.
Степенным рядом также называется функциональный ряд вида
(5)
ряд (5) есть степенной ряд по степенным двучлена (x-a).
Для определения области сходимости ряда (5) вводится замена переменного x-a=X и он принимает вид
(6)
Пусть интервал сходимости ряда (6) есть (-R,R). Тогда интервалом сходимости данного ряда (5) будет интервал (a-R, a+R) с центром в точке a. Все свойства степенного ряда (1) внутри интервала сходимости (-R,R) сохраняется и для степенного ряда (5) внутри интервала сходимости (a-R, a+R).
Пример 1. Найти область сходимости функционального ряда
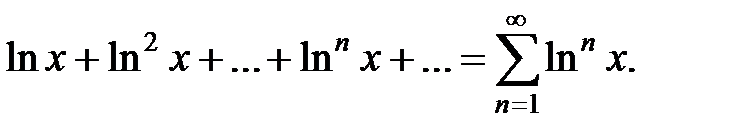
Решение:
Данный ряд является суммой членов геометрической прогрессии со знаменателем 
Такой ряд сходится, если 
т.е. при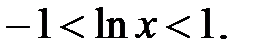 
Поэтому областью сходимости исследуемого ряда, является интервал. 
т.к. 
то 
.
т.к. каждому 
соответствует некоторое число – сумме числового ряда, то указанное соответствие определяет функцию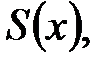 
которая называется суммой ряда (1) в области 
.