Дидактические единицы:
Основные понятия. Построение матрицы планирования в кодированной и натуральной формах и ее свойства. Рандомизация. Вычисление коэффициентов математической модели. Проверка коэффициентов на значимость. Проверка адекватности модели.
Основные понятия
Очень часто изучаемую систему представляют в виде следующей схемы:
Окружение
 |
Рис.1. Схема химико-технологической системы.
Рис. 1. Схема химико-технологической системы.
Если речь идет о химической системе, то такую систему называют химико-технологической системой (ХТС). Любая система взаимодействует с окружающей ее средой (окружением). Это проявляется в виде воздействия выходных параметров Y на окружение (например, загрязнение окружающей среды). В свою очередь, окружение так же воздействует на объект, внося в его работу помехи. На рис.1. это воздействие окружения на объект обозначается в виде возмущающих параметров 
. Например, воздействующими параметрами могут быть температура окружающего воздуха, атмосферное давление, световые лучи и другие параметры.
Входные параметры (факторы) -это такие параметры, которыми может управлять исследователь и которые определяют работу системы.
Под экспериментом (опытом) понимается совокупность операций, совершаемых над системой (объектом исследования), с целью получения информации об ее свойствах. Эксперимент, в котором исследователь по своему усмотрению может изменять факторы, называется активным экспериментом. Если исследователь не может самостоятельно изменять факторы, а лишь регистрирует их, то такой эксперимент называется пассивным экспериментом. В последнее время для моделирования и оптимизации различных процессов широко применяются методы активного планирования эксперимента.
План эксперимента – это совокупность опытов, которые необходимо выполнить при заданных условиях.
Планирование эксперимента – это целенаправленное управление экспериментом для достижения поставленных задач.
Цель планирования эксперимента заключается в нахождении таких условий и правил проведения опытов, при которых удается получить надежную и достоверную информацию о системе с наименьшей затратой труда, а также представить эту информацию в компактной аналитической форме с количественной оценкой точности.
Диапазоны изменения факторов задают их область. Если принять, что каждому фактору соответствует координатная ось, то полученное пространство называется факторным пространством.
Задачами активного планирования эксперимента является задача оптимизации, т.е. нахождение таких значений влияющих независимых переменных, при которой параметры оптимизации принимают экстремальные значения или задача построения математической модели объекта с целью предсказания его свойств. Далее рассмотрим вторую задачу более подробно.
Важнейшей задачей исследователя является задача построения математической модели изучаемой системы, т.е. в установлении связи между выходными и входными параметрами в виде функциональных зависимостей (функций отклика):
;
;
………………………....
.
В простейшем случае, когда имеется только один выходной параметр (Y) математическая модель в общем виде можно представить следующим уравнением:
.
Как правило, математическая модель записывается в виде полинома некоторой степени:
,
где 
– выходная переменная; 
– входные переменные (
); 
– число факторов. Данное уравнение называется уравнением регрессии, а коэффициенты – 
коэффициентами регрессии. Например, для двух факторов эта зависимость может имеет следующий вид:
При первоначальном исследовании системы обычно применяют более простые -линейные уравнения регрессии:
Например, для трех факторов:
Далее будет рассмотрен алгоритм построения линейных моделей с использованием механизма ПФЭ.
ПФЭ – это эксперимент, в котором реализуется все возможные сочетания уровней факторов. Уровень фактора это значение фактора, которое поддерживается в течение всего опыта. В полном факторном эксперименте используется два уровня фактора: нижний и верхний. Например, фактор 
может принимать два уровня: +80 (нижний) и +120 (верхний). Эти уровни задает исследователь. Кроме верхнего и нижнего уровня используется нулевой (основной) уровень (центр экспериментирования).
Исследователь должен также для каждого фактора выбрать интервал варьирования 
. Интервал варьирования – это такая величина прибавление которой к основному уровню фактора дает верхний уровень фактора, а вычитание из основного уровня дает нижний уровень фактора. Основное преимущество факторного эксперимента заключается в том, что в эксперименте варьируются одновременно все факторы.
Достоинства полного факторного эксперимента:
- независимость дисперсии переменной состояния от вращения системы координат в центре плана;
- одинаковая и минимальная дисперсию коэффициентов регрессии;
- независимость определения коэффициентов регрессии друг от друга;
- простота вычисления коэффициентов.
План эксперимента, в котором указаны значения нижнего и верхнего уровней всех факторов, называется ПФЭ типа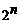 
, где 
– число факторов, а 2 – число уровней.
Матрица планирования
План эксперимента удобно изображать в виде матрицы планирования, состоящей из 
строк и 
столбцов. Каждая строка матрицы соответствует опыту, а столбец – определенному фактору.
Матрица планирования может быть записана в кодированной форме в виде чисел +1 и -1 или в натуральной форме в виде натуральных значений факторов (температуры, давления, концентрации компонентов).
На примере двух факторов (n=2) рассмотрим, как составляется матрица планирования. Для ПФЭ типа 22 общее число опытов равно 4.
Таким образом, получается следующая матрица планирования для двух факторов (таблица 1)
Таблица 1:
| № опыта | X1 кодир | X2кодир | X1натур | X2натур |
| -1 | -1 | 0.5 | ||
| +1 | -1 | 0.5 | ||
| -1 | +1 | 1.5 | ||
| +1 | +1 | 1.5 |
В данной матрице каждый кодированный элемент имеет два индекса 
, где 
– номер строки, а 
– номер столбца.
Можно заметить, что у первого фактора знак все время чередуется, а у второго фактора чередуется через два элемента. (При наличии третьего фактора чередование знака происходило бы уже через четыре элемента!)
Для определения натурального значения фактора пользуются следующей формулой:
,
где 
- значение фактора в натуральной форме, соответствующее основному (нулевому) уровню фактора; 
- значение фактора в кодированной форме.
Например, если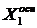 
=20, 
=5, 
= -1, то 
=20+5*(-1)=15;
Если 
=1, 
=0.5, 
=-1, то 
=1+0.5*(-1)=0.5
Из построения матрицы планирования вытекают два следствия. Для каждого столбца (записанного в кодированной форме) выполняется свойства симметричности и нормировки:
- свойство симметричности. (Сумма элементов каждого столбца равна нулю);
, 
- свойство нормировки. (Сумма квадратов элементов каждого столбца равна числу опытов ПФЭ),
где - число факторов; 
- число опытов (или строк матрицы планирования).
Эти условия легко проверить непосредственно по матрице планирования.
Кроме этих свойств существует еще одно важное условие, это условие ортогональности, которое предполагает равенство нулю суммы произведений любых двух столбцов матрицы:
Это условие также легко проверить. Действительно, полный факторный эксперимент типа 
является ортогональным.
Для удобства расчета свободного члена b0 в матрицу планирования вводят столбец кодированных значений, который соответствует так называемому фиктивному фактору. Физического смысла этот фактор не имеет, но позволяет легко вычислить коэффициент уравнения b0.
Тогда матрица планирования имеет следующий вид:
| № опыта | X0 кодир | X1 кодир | X2кодир | X1натур | X2натур |
| +1 | -1 | -1 | 0.5 | ||
| +1 | +1 | -1 | 0.5 | ||
| +1 | -1 | +1 | 1.5 | ||
| +1 | +1 | +1 | 1.5 |
Геометрическое отображение плана ПФЭ для двух факторов (
) в факторном пространстве:
 |
|
|
|
|
Точки плана располагаются в вершинах квадрата.
После построения матрицы планирования приступают к эксперименту. Обычно матрицу планирования представляют в виде, удобном для реализации опытов – все кодированные значения факторов заменяют натуральными. Такую матрицу планирования называют рабочей матрицей планирования.
Поскольку на изменение параметра оптимизации влияют помехи (возмущающие факторы), план чаще всего реализуют несколько раз, получая 
параллельных значений переменной величины.
Рандомизация
Опыты в матрице планирования проводится в случайном порядке. Такая операция очень часто используется в планировании эксперимента с целью уменьшения систематической ошибки. Для проведения опытов в случайном порядке используют таблицу случайных чисел.
Расчет ошибки опыта.
Расчет ошибки ПФЭ по результатам опытов в центре плана
Для вычисления ошибки эксперимента проводят серию параллельных опытов No в любой точке плана (чаще всего в центре плана):
. 
Корень квадратный из дисперсии - (S) – это ошибка опыта:
Полученную величину S используют в дальнейших расчетах при проверке коэффициентов на значимость и проверке модели на адекватность.
Расчет ошибки по результатам параллельных опытов матрицы планирования
Если в матрице планирования все эксперименты проводились одинаковое число раз, то можно проверить однородность построчных дисперсий. Это позволяет судит о качестве проделанной работы и рассчитать ошибку опыта.
Итак, пусть матрица планирования содержит N опытов, каждый из которых продублирован m раз.
| YY11 | YY12 | Y13 | ……. | Y1m | |
| YY21 | YY22 | Y23 | ……. | Y2m | |
| YY31 | YY32 | Y33 | ……. | Y3m | |
| ……. | ……. | …. | ……. | …. | |
| N | YN1 | YN2 | YN1N2 | ……. | YNm |
Вычисляются построчные дисперсии для каждой сроки матрицы
где, 
- среднеарифметическое значение i параметра оптимизации, определяемое в каждой строке плана
Вычисляется расчетное значение критерия Кохрена:
,
где 
- максимальная построчная дисперсия;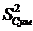 
- сумма всех построчных дисперсий.
Расчетное значение критерия Кохрена сравнивается с табличным значением:
G рас < G таб (N, f=m-1, α)
- α уровень значимости, обычно задается 0.05).
Расчет коэффициентов уравнения регрессии при равном числе параллельных опытов в каждой точке факторного пространства
Коэффициенты находятся по формуле:
,
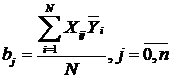где 
- среднее значение параметра оптимизации, вычисленное по параллельным опытам – ой строки матрицы планирования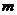 
.
Проверка значимости коэффициентов регрессии.
Очевидно, что один фактор больше влияет на параметр оптимизации, другой – меньше. Поэтому можно проверить полученные коэффициенты регрессии на значимость, т.е. оценить величину влияния каждого фактора на значение параметра оптимизации. Если эта величина соизмерима с ошибкой эксперимента, то соответствующий коэффициент не несет дополнительной информации об объекте, и его можно приравнять к нулю, что упрощает математическую модель.
Значимость коэффициентов проверяется с помощью 
– критерия Стьюдента.
Значения – критерия вычисляются для каждого для каждого фактора по формуле:
, 
Полученные значения сравнивают с табличным значением критерия Стъюдента 
, которое находится по числу степеней свободы 
, и уровню значимости α - величина, характеризующая вероятность того, что решение будет неправильным. Обычно принимают, что 
α =0.05.
Если
> 
,
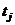то коэффициент значимо отличается от нуля, если же 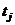< , то коэффициент приравниваются к нулю: 
.
В результате выполнения этого этапа моделирования получают уравнение регрессии, включающее значимые коэффициенты регрессии 
.
Проверка адекватности линейного уравнения регрессии
Проверку адекватности уравнения регрессии проводят по 
- критерию Фишера. Суть этой проверки сводится к сравнению двух дисперсий: дисперсии адекватности 
и дисперсии воспроизводимости 
. Если первая величина соизмерима со второй, то можно считать, это уравнение адекватно описывает экспериментальные данные. В противном случае оно не адекватно – тогда необходимо либо уменьшить интервал варьирования 
, либо увеличить порядок уравнения регрессии.
Дисперсия адекватности определяется по формуле:
,
где 
- расчетные значения, получаемые по уравнению регрессии,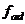 
- число степеней свободы 
, где 
- число значимых коэффициентов).
Затем вычисляют расчетное значение критерия Фишера ( - критерия):
Расчетное значение критерия Фишера сравнивают с табличным значением 
, найденным при степенях свободы 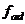и 
, и заданном уровне значимости α. Если выполняется условие
> , (1)
то линейное уравнение регрессии признается адекватным. Если это условие не выполняется, т.е. < , то уравнение считается неадекватным.
При расчете F предполагается что 
. Если наблюдается обратное, то вывод об адекватности может быть сделан и без проверки условия (1).
Если модель адекватна, то ее можно использовать для поиска области оптимума объекта исследования или для предсказания отклика.
При неадекватной линейной модели наиболее часто принимают решение об уменьшении интервалов варьирования факторов и повторении эксперимента