Теорема Остроградского-Гаусса

Скалярное поле

Термин "поле" обычно употребляется в физике для обозначения части пространства (или всего пространства), в которой рассматривается некоторое физическое явление. Если речь идет о процессе, характеризующемся скалярной величиной (температура, давление и т.д.), поле называется скалярным.

Определение. Числовая функция , заданная в каждой точке некоторой пространственной области , называется скалярным полем (то есть каждой точке этой области ставится в соответствие число ).

Введя в области, где задано скалярное поле, декартовы координаты, можно представить это поле в виде функции , определенной в области . Если поле задано функцией двух переменных , то оно называется плоским. Эту функцию мы всегда в дальнейшем будем предполагать непрерывной и имеющей непрерывные частные производные первого порядка по всем переменным.

Можно добавить, что величина , характеризующая скалярное поле, может зависеть не только от координат точки , но также и от времени. Однако мы ограничимся рассмотрением лишь таких полей, где не зависит от времени. Такие поля называются стационарными.

Примерами скалярных полей могут служить:
1) поле температур некоторого нагретого тела (в каждой точке этого тела задана соответствующая температура ),
2) потенциал электростатического поля задается формулой

,

где - заряд, а - расстояние от произвольной точки до заряда, помещенного в начало координат,
3) поле давлений,
4) поле плотности вещества и др.

Геометрической характеристикой скалярного поля служат поверхности уровня – множества точек пространства, в которых функция принимает постоянное значение: – уравнение различных поверхностей уровня при различных значениях .
В плоском поле – уравнение линий уровня. С помощью линий уровня обычно изображаются рельеф местности на топографических картах, а именно, на них проводятся линии, состоящие из точек, имеющих одну и ту же высоту над уровнем моря (эти линии называются горизонталями). Распределение температур, давления, количества осадков и т.п. обычно также изображаются на специальных картах с помощью соответствующих линий уровня (они называются изотермами в случае поля температур или изобарами в случае поля давления).

Пример 1. Построить поверхности уровня потенциала электростатического поля .
Решение.
Так как , то поверхности уровня будут задаваться так:

или ,

где - некоторое положительное число, при этом для электростатического поля заряд есть величина постоянная.
Возведем в квадрат обе части последнего равенства и получим уравнение сферы с центром в начале координат и переменным радиусом :

.

Значит, поверхностями уровня электростатического поля будет семейство концентрических сфер с центром в точке, где находится заряд .

При изучении скалярного поля методами анализа мы должны в первую очередь описать его локальные свойства, т.е. изменение величины при переходе от данной точки к близким точкам. Для этого используют понятие производной по направлению.

Пусть скалярное поле определено в области .
Зафиксируем точку и выберем некоторое направление, определяемое вектором ; если существует предел , то его называют производной функции по направлению в заданной точке , где , , .

Пусть скалярная функция дифференцируема в точке . Производную функции в точке по направлению вектора вычисляют по формуле

,

где – направляющие косинусы вектора .
Производная поля в данной точке по направлению характеризует скорость изменения поля в этом направлении.

Пример 2. Найти производную скалярного поля в точке в направлении вектора .
Решение.
Для нахождения производной по направлению будем использовать формулу
Найдем частные производные заданной функции: .
Вычислим значения частных производных в заданной точке , т.е. при , и :
.
Найдем значения направляющих косинусов:
,
поэтому .
Подставим все найденные величины в расчетную формулу для производной по направлению и получим:
.
Ответ: .

Можно установить, что по направлению, касательному к поверхности уровня, производная от заданной функции равна нулю. Чтобы в этом убедиться, достаточно рассмотреть кривую, лежащую на поверхности уровня. Вдоль такой кривой приращение функции равно нулю , т.к. на поверхности уровня значения функции постоянны. Поэтому .

Определение. Градиентом скалярного поля в точке называется вектор

Между производной поля по направлению и градиентом в точке существует следующая связь:

,

где - орт вектора , т.е. единичный вектор, сонаправленный с вектором .

Из этого равенства следует, что в каждой точке , не являющейся критической, градиент направлен в сторону максимального возрастания поля , а модуль градиента равен величине скорости этого возрастания:

.

Свойства градиента.
1) ,
т.е. градиент алгебраической суммы скалярных полей и есть сумма градиентов указанных полей. Это свойство непосредственно вытекает из определения градиента, т.к. производная суммы равна сумме производных.

2) Градиент произведения скалярных полей .
В правой части последнего равенства стоит сумма векторов, где и - скалярные множители.

3) , где - постоянное произвольное число,
т.е. постоянный множитель можно выносить за знак градиента.

4) Градиент частного скалярных полей .

5) Градиент сложной функции .

В правых частях всех свойств знаки и обозначают сложение и вычитание векторов, а знак произведения - есть произведение вектора на скаляр.

Пример 3. Найти градиент потенциала электростатического поля, образованного точечным зарядом, помещенным в начало координат:

, где .

Решение.
Для нахождения градиента будем использовать формулу .
Найдем проекции градиента, т.е. частные производные скалярного поля:
.
Аналогично можно найти .
Поэтому искомый градиент будет равен:
, где есть радиус-вектор произвольной точки пространства.
Знак "минус" говорит о том, что градиент потенциала электростатического поля направлен противоположно радиус-вектору произвольной точки поля. Т.к. поверхностями уровня поля являются концентрические сферы, а нормаль сферы совпадает с ее радиусом, то градиент направлен по радиусу сферы к ее центру.

Вопрос. Максимальное значение производной по направлению скалярного поля в точке равно

 

Виды скалярных полей

Во многих физических задачах приходится иметь дело с полями, обладающими теми или иными специальными свойствами симметрии, облегчающими изучение таких полей. Укажем некоторые частные случаи.

Плоскопараллельное поле
Если скалярное поле в какой-либо декартовой системе координат можно описать функцией, зависящей не от трех, а от двух координат, т.е. , то такое поле называется плоскопараллельным (или двумерным).

Т.е. поле будет плоскопараллельным, если в пространстве существует направление, при сдвигах вдоль которого поле переходит само в себя. Поверхности уровня такого поля - это семейство цилиндрических поверхностей, причем в соответствующим образом выбранной системе координат они задаются уравнениями вида 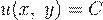, где - произвольное число.

Осесимметрическое поле
Если для поля можно подобрать такую цилиндрическую систему координат, в которой оно изображается функцией, зависящей только от переменных и , но не от угла , то это поле называется осесимметрическим.

Иначе говоря, поле является осесимметрическим, если оно переходит само в себя при повороте пространства на произвольный угол вокруг некоторой фиксированной прямой - оси симметрии этого поля. Поверхности уровня такого поля представляют собой поверхности вращения.

Если эти поверхности вращения - круглые цилиндры, т.е. поле в цилиндрической системе координат задается функцией, зависящей ишь от одной координаты , то поле называется цилиндрическим.

Сферическое поле
Если значения поля зависят лишь от расстояния точки до некоторой фиксированной точки , то такое поле называется сферическим полем.

Поверхности уровня такого поля - семейство концентрических сфер.

Вопрос. Скалярное поле потенциала электрического заряда , задаваемого формулой , где , является

Плоскопараллельным

Сферическим

Цилиндрическим

Осесимметрическим

 

Векторное поле

Определение. Если в каждой точке пространственной области задан определенный вектор , то говорят, что в этой области задано векторное поле.

Если в пространстве выбрать декартову систему координат, то векторное поле задается тремя скалярными полями (функциями) , являющимися проекциями вектора на координатные оси декартовой системы:

.

Векторное поле тоже может быть плоским, например, .
В дальнейшем будем рассматривать векторные поля, компоненты которых непрерывны и имеют непрерывные частные производные первого порядка.

Примерами векторных полей могут служить:
1) поле скоростей стационарного потока жидкости (оно определяется так: пусть область заполнена жидкостью, текущей текущей в каждой точке с некоторой скорость , не зависящей от времени, но различной в разных точках области; тогда поставив в соответствие каждой точке вектор , получим векторное поле скоростей жидкости);
2) поле тяготения (пусть в пространстве распределена некоторая масса, тогда на материальную точку единичной массы действует гравитационная сила);
3) электрическое поле (если в пространстве распределены каким-либо образом заряды, то на единичный электрический заряд, помещенный в точку , эти заряды действуют с определенной силой .

Определение. Векторной линией поля называется такая линия, в каждой точке которой касательная направлена вдоль заданного в этой точке вектора поля.

Если векторное поле есть поле скоростей жидкости, то векторные линии - это траектории частиц жидкости.

Напряженность электростатического поля определяется вектором , где - электрический заряд, - радиус-вектор направления, соединяющего заряд с точкой поля. Поэтому для положительного заряда векторными линиями будут лучи, выходящие из заряда.

Для магнитного поля векторными линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.

Найдем уравнения векторных линий. Пусть есть радиус-вектор какой-нибудь векторной линии. Тогда вектор направлен по касательной к ней. По определению векторного поля векторы и должны быть коллинеарны, откуда следует пропорциональность их проекций. Поэтому всякое векторное поле обладает семейством векторных линий. Уравнения этого семейства есть общее решение дифференциальных уравнений вида

Замечание. Если векторное поле плоское, то дифференциальное уравнение векторных линий имеет вид:

В силу теоремы существования и единственности через каждую точку , при соблюдении условий этой теоремы, будет проходить одна определенная векторная линия. Если провести все векторные линии, проходящие через все точки некоторого куска поверхности , то их совокупность даст векторную трубку. Причем нормаль к векторной трубке в некоторой точке ортогональна вектору , т.е. .

Пример 1. Для плоского векторного поля найти уравнения семейства векторных линий и векторной линии, проходящей через точку .
Решение.
Так как и , то, согласно замечанию, уравнение семейства определяется общим решением дифференциального уравнения

.

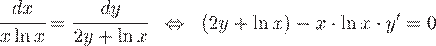Это уравнение линейное первого порядка. Решая его методом вариации произвольной постоянной, получим общее решение в виде .
Выделим из этого семейства одно решение – то, которое представляет собой уравнение векторной линии, проходящей через точку . Подставив в общее решение и , получим . Итак, искомая векторная линия (синим цветом на чертеже отмечена точка с координатами ).

Пример 2. Определить векторные линии магнитного поля, образованного постоянным электрическим током с силой , текущим по бесконечно длинному прямолинейному проводу.
Решение.
Если принять провод за ось , то вектор напряженности магнитного поля выражается формулой
где - расстояние от произвольной точки до провода.
В данном случае .
Поэтому дифференциальные уравнения векторных линий примут вид:

,

здесь сократили на общий множитель .
Последняя система равносильна системе

Значит, векторные линии напряженности магнитного поля определяются уравнениями и , где и - константы. Эти линии являются окружностями с центрами на оси , лежащими в плоскостях, перпендикулярных этой оси.

Вопрос. Векторными линиями векторного поля являются

семейство гипербол

семейство прямых

семейство эллипсов

семейство парабол

Поток векторного поля

Пусть в поле вектора задана ориентированная поверхность . Обозначим через единичный вектор нормали к выбранной стороне поверхности в ее произвольной точке.

Если для наглядности считать, что вектор - вектор скорости несжимаемой жидкости, движущейся стационарно, а поверхность находится в этой жидкости. Подсчитаем количество жидкости, протекающей через эту поверхность за единицу времени.

Для этого разобьем поверхность на элементарных поверхностей , ,..., . В каждой из этих поверхностей выберем точку , отложим от нее вектор нормали . Условимся при этом, что если замкнутая поверхность, то берется по направлению внешней нормали. Если же незамкнута, то выберем произвольно направление нормалей так, чтобы они лежали по одну сторону от поверхности. Поверхности в силу их малости можно считать плоскими, а вектор постоянным во всех точках и равным .

Поэтому количество жидкости , протекающей через поверхность , будет приблизительно равно объему цилиндрической фигуры с основанием и и образующей , т.е.

,

где - проекция вектора на нормаль и - площадь поверхности .

Общее количество жидкости , протекающей через поверхность в единицу времени, равно сумме количеств жидкости, протекающей через все элементарные поверхности. Поэтому будем иметь:

Если существует предел полученных интегральных сумм при неограниченном увеличении числа элементов разбиения поверхности и при стремлении диаметра разбиения (т.е. наибольшего размера поверхностей, входящих в разбиение) к нулю, то он является поверхностным интегралом функции по поверхности и обозначается .

Определение. Поверхностный интеграл 1 рода по поверхности от скалярного произведения вектора на вектор называется потоком векторного поля через ориентированную поверхность и обозначается :

В случае замкнутой поверхности поток записывается в виде .

Если ввести в рассмотрение вектор и обозначить его проекции на оси координат , то формулу для потока можно переписать в виде

,

где вектор направлен по нормали к выбранной стороне поверхности . Правая часть последнего равенства является поверхностным интегралом 2 рода.

Если, например, – поле скоростей текущей жидкости в области и – незамкнутая поверхность с выбранным направлением нормали , то поток равен количеству жидкости, проходящей в единицу времени через поверхность в направлении вектора . Если – замкнутая поверхность, ограничивающая некоторую область с внешней нормалью , то поток равен разности количеств втекающей в эту область жидкости и вытекающей. В случае, если поток 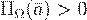, то в области имеются источники (где векторные линии порождаются), а если , то это указывает на наличие в области стоков (где векторные линии заканчиваются). А если , тогда либо нет ни источников ни стоков, либо источники и стоки уравновешивают друг друга.

Если ориентированная поверхность задана явно непрерывно дифференцируемой функцией , где , то можно получить следующую формулу, связывающую поверхностный интеграл по поверхности с двойным интегралом по проекции этой поверхности на плоскость :

,

где знак «плюс» берется, когда угол острый.
Если поверхность задана явно уравнением , где или , где , то соответственно меняются роли переменных в последней формуле.

Пример. Найти поток векторного поля через часть поверхности параболоида , отсеченной плоскостью , если нормаль к заданной поверхности составляет тупой угол с осью аппликат.
Решение.
Поток векторного поля будем искать по формуле , где – единичный вектор нормали к заданной поверхности , угол , область – проекция поверхности на плоскость .

Для поверхности или нормаль , тогда единичный вектор нормали , В данном случае , т.е. (тупой угол).
Найдем скалярное произведение :
.
Т.к. проекцией заданной поверхности на плоскость является круг радиуса (потому что ), то при вычислении соответствующего двойного интеграла необходимо будет перейти в ПСК (полярную систему координат).
Вычислим требуемый поток векторного поля:

ПСК
.

Вопрос. Поток векторного поля через часть плоскости , лежащей в первом октанте, т.е. при , (нормаль составляет острый угол с осью )

выражается формулой

 

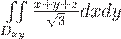
Дивергенция

Рассмотрим векторное поле и некоторую замкнутую поверхность в этом поле. Допустим, что поток вектора через внешнюю сторону поверхности положителен, т.е. .

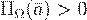Если рассматривать заданное векторное поле как поле скоростей движущейся жидкости, то положительность потока указывает, что количество жидкости, вытекающей из тела , заключенного внутри замкнутой поверхности , больше, чем количество жидкости, втекающей в это тело. То есть внутри тела должны находиться источники поля, обильность (или интенсивность) которых характеризуется величиной потока через . Аналогично в случае отрицательного потока внутри тела должны находиться стоки. Характеристикой интенсивности источника или стока служит средняя удельная интенсивность, которая определяется отношением потока вектора через замкнутую поверхность к объему тела , ограниченного поверхностью: .

Чтобы получить характеристику удельной интенсивности источника (или стока) в каждой отдельной точке, поступают так. Рассмотрим некоторую точку векторного поля и заключим ее внутри небольшой замкнутой поверхности (например, внутри сферы достаточно малого радиуса). Объем тела, ограниченного поверхностью обозначим . Разделив поток вектора через замкнутую поверхность на объем , получим среднюю удельную интенсивность . Предел этой величины, когда объем стремится к нулю и стягивается в точку , если такой предел существует, называют дивергенцией вектора и обозначают .

Определение. Дивергенцией векторного поля в точке называется предел отношения потока поля через замкнутую поверхность , окружающую точку , к объему тела , ограниченного этой поверхностью, при стремлении диаметра