Под линейными операциями над векторами понимают операции сложения векторов и умножение их на число.
Геометрическая интерпретация. Пусть  и
и  два произвольных вектора. Возьмем произвольную точку O и построим из нее вектор
два произвольных вектора. Возьмем произвольную точку O и построим из нее вектор  . От точки A отложим вектор
. От точки A отложим вектор  . Вектор
. Вектор  , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов  и
и  :
:  (рис. IV.1).
(рис. IV.1).
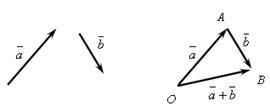
Рис. IV.1
Это правило сложения векторов называется правилом треугольника. Аналогично происходит сложение нескольких векторов (рис IV.2):
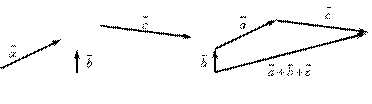
Рис. IV.2
Под разностью векторов  и
и  понимается вектор
понимается вектор  . На практике вектора
. На практике вектора  и
и  откладывают из одной точки, концы соединяют и вектор имеет направление «к концу вектора
откладывают из одной точки, концы соединяют и вектор имеет направление «к концу вектора  ».
».
Отметим, что в параллелограмме (рис. IV.3), построенном на векторах  и
и  , одна направленная диагональ является суммой векторов
, одна направленная диагональ является суммой векторов  и
и  , а другая - разностью.
, а другая - разностью.

Рис. IV.3
Произведением вектора  на скаляр (число) λ,
на скаляр (число) λ,  , называется вектор
, называется вектор  , который имеет длину вектора
, который имеет длину вектора  , умноженную на λ, а направление совпадает с направлением вектора
, умноженную на λ, а направление совпадает с направлением вектора  , если
, если  , и противоположно направлению вектора
, и противоположно направлению вектора  , если
, если  .
.
Линейные операции над векторами обладают следующими свойствами:
1)  ; ;
| 3)  ; ;
|
2)  ; ;
| 4) 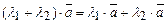 ; ;
|
5) 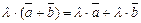 , ,  . .
|
Эти свойства позволяют проводить преобразования над векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
Проекция вектора на ось
Прямая с заданной на ней точкой и единичным базисным вектором  называется осью.
называется осью.
Ортогональной проекцией точки A на ось называется точка пересечения оси с перпендикулярной к ней плоскостью, проходящей через точку А.
Пусть в пространстве задана направленная прямая l. Проекцией точки М на ось l называется основание  перпендикуляра
перпендикуляра  , опущенного из точки М на ось. Если точка М лежит на оси l, то проекция точки М на ось совпадает с М (рис. IV.4).
, опущенного из точки М на ось. Если точка М лежит на оси l, то проекция точки М на ось совпадает с М (рис. IV.4).

Рис. IV.4
Пусть  – произвольный вектор. Проекцией вектора
– произвольный вектор. Проекцией вектора  на ось l называется координата вектора
на ось l называется координата вектора  относительно единичного вектора
относительно единичного вектора  оси, где А 1 и В 1 – проекции точек A и B на ось l, то есть если
оси, где А 1 и В 1 – проекции точек A и B на ось l, то есть если 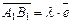 , то число l называется проекцией вектора
, то число l называется проекцией вектора  на ось l, в направлении
на ось l, в направлении  . Обозначение для проекции:
. Обозначение для проекции:  .
.
Из правил сложения векторов и умножения вектора на число, заданных своими координатами, следует, что:
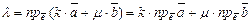 , где
, где  .
.
Легко показать, что  , где j – угол между векторами
, где j – угол между векторами  и
и  , отсчитываемый по правилам тригонометрии: от вектора
, отсчитываемый по правилам тригонометрии: от вектора  против часовой стрелки до вектора
против часовой стрелки до вектора  .
.
Следует помнить: проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол прямой.
Действия над векторами, заданными проекциями, выполняются аналогично действиям над матрицей-строкой (матрицей-столбцом).
Рассмотрим 3-х мерное линейное пространство L и  (рис. IV.5). Введем декартову систему координат Oxyz. Представим вектор
(рис. IV.5). Введем декартову систему координат Oxyz. Представим вектор  в виде линейной комбинации базисных векторов
в виде линейной комбинации базисных векторов  ,
,  ,
, 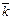 :
:
 . (IV.1)
. (IV.1)
Проекцией вектора  на ось Ox называется величина направленного отрезка
на ось Ox называется величина направленного отрезка 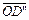 и записывается
и записывается  .
.
Так как, по определению,  , то если
, то если  – угол между осью Ox и вектором
– угол между осью Ox и вектором  , то
, то
 . (IV.2)
. (IV.2)
Аналогично определяются проекции вектора  на другие оси.
на другие оси.

Рис. IV.5.
Сопоставляя (IV.1) и (IV.2) и учитывая, что проекция есть направленный отрезок (если  , то
, то  ), то
), то
 ,
,  ,
,  .
.
Заметим, что 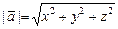 , получаем
, получаем
 ,
,  ,
,  . (IV.3)
. (IV.3)
 ,
,  ,
,  называются направляющими косинусами. Возводя в квадрат и складывая, получим
называются направляющими косинусами. Возводя в квадрат и складывая, получим
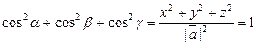 ,
,
то есть сумма квадратов направляемых косинусов равна 1:
 . (IV.4)
. (IV.4)
Пусть углы вектора  с осями Ox, Оу, Оz соответственно равны a, b, g. По свойству проекции вектора на ось имеем:
с осями Ox, Оу, Оz соответственно равны a, b, g. По свойству проекции вектора на ось имеем:
 ,
,  ,
, 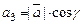 .
.
или, что то же самое:
 ,
,  ,
, 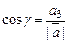 . (IV.5)
. (IV.5)
Числа  ,
,  ,
,  называются направляющими косинусами вектора
называются направляющими косинусами вектора  (
( ).
).