Цилиндрические (полуполярные) координаты в пространстве.

Выделим точку М в пространстве . В плоскости , в которой принимается полярная система координат, определяется положение точки N (проекция точки М на плоскость ). Положение точки относительно плоско­сти определяется координатой z. Тогда координатами точки М в пространстве будут три числа: , где определяет положе­ние точки М над плоскостью – смотри рисунок, а величины тождественны полярным координатам точки в плоскости .

Обычно будем считать, что угол изменяется в диапазоне: , а расстояние точки до полюса O – в диапазоне: . Диапазон изменения координаты вполне очевиден: .

Замечания: цилиндрические координаты некоторые авторы называют ещё полуполярными.

Совместим полюс цилиндрической системой координат и начало O прямоугольной системы координат. Пусть также полярная ось ОХ цилиндрической системы совпадает с осью OX декартовых координат, а ось с осью декартовых координат.

Используя рисунок, нетрудно записать выражения для перехода от одних координат выделенной точки к другим:

1). От цилиндрических координат к декартовым координатам: (10)

2). От декартовых координат к цилиндрическим координатам:

, , . (11)

Замечания: 1) из выражений (11) необходимо учитывать и выражение для косинуса, и выраже­ние для синуса, так как только так можно однозначно определить по­ложение луча, содержащего выделенную точку;

2) следует учесть также, для на­чала координат из выра­жений (11) угол опреде­лить не удаётся: нару­шается взаимно однозначное соответствие систем коорди­нат.

Полярные (сферические) координаты в пространстве.

В этом случае положение точки М в про­странстве определяется тремя числами – показано на рисунке. Постоянными элементами, относительно которых определяется положе­ние любой фигуры пространства, являются: полюс – точка O; полярная ось – ось ОZ; полярная полуплоскость – плоскость .

Обычно будем считать, что угол изменяется в диапазоне: , угол изменяется в диапазоне: , а расстояние точки до полюса O – в диапазоне: . Применяемые диапазоны изменения координат обеспечивают взаимно однозначное соответствие всех точек, определяющих геометрические фигуры, и их координат – аналитических моделей!

Используя рисунок, нетрудно записать выражения для перехода от сферических координат к прямоугольным декартовым координатам:

1). От цилиндрических координат к декартовым координатам: (12)

2). От декартовых координат к цилиндрическим координатам:

, , , . (13)

Замечания: 1) из выражений (13) необходимо учитывать и выражение для косинуса, и выраже­ние для синуса, так как только так можно однозначно определить по­ложение луча, содержащего выделенную точку;

2) следует учесть также, для на­чала координат ( =0) из выра­жений (13) углы опреде­лить не удаётся: нару­шается взаимно однозначное соответствие систем коорди­нат;

3) специальные системы координат часто применяют в физике; эффективно их при­меняют и в математическом анализе.

Представленные ниже задачи иллюстрируют преобразование и использование систем координат.

☺☺

Пример Д – 4: Начало координат перенесено (без изменения направления осей) в точку . Координаты точек = (1,3), = (–3,0) и =(–1,4) определены в новой системе. Вы­числить координаты этих же точек в старой системе координат.

Решение:

1). Имеем на плоскости системы координат: , и . Система координат получается параллельным переносом системы . Система координат по­лу­ча­ется вращением системы на угол , причём за положительное направление вращение принято вращение оси против часовой стрелки.

Определим для принятых систем координат базисные векторы. Так как система получена параллельным переносом системы , то для обеих этих систем примем базисные векторы: , причём единичные и совпадающие по направлению с осями координат , , соответственно. Для системы в качестве базисных векторов примем единичные векторы , совпадающие по направлению с осями , .

Результат преобразования системы координат в систему координат представлен в выражениях:

при =0 → (1.1)

2). По условию задачи: a =3, b =–4 и =0. Тогда (1.1) принимают вид:

3). Используя полученные формулы, вычислим координаты заданных точек в старой системе координат : = (4,–1), = (0,–4) и =(2, 0).

Ответ: = (4,–1), = (0,–4), = (2, 0).

Пример Д – 5: Начало координат неподвижно, координатные оси повёрнуты на угол =60⁰. Коор­динаты точек = (2 ,–4), = (,0) и =(0,–2 ) определены в новой системе. Вычислить координаты этих же точек в старой системе координат.

Решение:

1). Воспользуемся формулами, приведёнными в Примере Д – 4 для случая a =0, b =0 и =60⁰:

→ (1.1)

2). В формулы (1.1), подставим координаты точек , , . После несложных вычислений получим координаты этих точек в системе координат :

= , = , = .

Ответ: = , = , = .

Пример Д – 6: Две системы координатных осей , имеют общее начало O и преобра­зуются одна в другую поворотом на некоторый угол. Координаты точки = определены относительно первой из них. Вывести формулы преобразования коор­динат, зная, что положительное направление оси определено отрезком .

Решение:

1). В системе координат задана точка = . Будем считать, что перед преобразованием имеем совпадающие системы координат и . К системе координат применено преобразование вращения так, что относительно исходного своего положения, то есть относительно системы , эта система оказывается повёрнутой на угол . В системе координат координаты точки составляют пару чисел: . Для рассматриваемого случая были получены выражения, определяющие связь координат точки в системах координат: и :

(1)

2). Используя вектор , найдём: = , =– 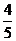, после чего формулы преобразова­ния координат:

откуда: (F)

Ответ: текст: формулы (F).

Рассмотренные Примеры Д – 1 Д – 6 иллюстрирует переходы от одной системе координат к другой с использованием готовых формул и получением в рамках заданных условий.

☻