Как было показано наиболее эффективным методом решения уравнения на этапе проекции является многосеточный метод, вычисления в котором ведутся на сетках различной грубости. В AmgX нет возможности использовать информацию о геометрических свойствах сетки, но геометрическая вариация многосеточного метода эффективнее алгебраической [18], а также потребляет значительно меньше памяти. Следовательно, в свете вышеизложенной информации наиболее выгодным видится использование именно геометрического многосеточного метода.
Суть метода заключается в том, что уточнение приближенного решения на сетках более грубых по сравнению с целевой, позволяет увеличить скорость сходимости за счет уменьшение погрешности по всем частотам спектра разностного оператора [15].
Обозначим точное решение разностной задачи на сетке с шагом  за
за  , разностный оператор Лапласа за
, разностный оператор Лапласа за  , погрешность решения на той же сетке за
, погрешность решения на той же сетке за  , а приближенно решение, за
, а приближенно решение, за  . Тогда
. Тогда  . Подставим точное решение в исходную задачу.
. Подставим точное решение в исходную задачу.

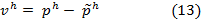
Тогда:

где  .
.
Полученное уравнение можно приближенно решить уже на более грубой сетке, а затем интерполировать его приближенное решение на изначальную сетку и сложить с приближенным решением исходной задачи, тем самым приблизив его к точному. Данную процедуру можно повторить для каждой сетки.
Имея это в виду, отметим, что при использовании некоторых численных методов на первых итерациях уменьшение вектора ошибки происходит независимо от величины шага сетки h. Такие методы называются сглаживателями [15].
Таким образом мы приходим к понятию V-цикла. Сначала выполняется несколько итераций сглаживателя на самой детализированной сетке. Затем вычисляется невязка, которая огрубляется на сетку следующая уровня и итерации сглаживания повторяются уже на ней. Итерации повторяются до тех пор, пока не будет достигнута самая грубая сетка. После этого результаты интерполируется на более точные сетки и складываются с приближенными решениями на них до тех пор, пока не будет достигнута самая точная сетка.

Рисунок 2: V-цикл [19]
Способ, когда самая точная сетка не достигается с первого раза, а начиная с некоторого уровня вновь происходит огрубление, называется W-циклом. Последовательная комбинация V-циклов, которая начинается на самой грубой сетке и с каждым новым V-циклом достигает все более точных сеток, называется полным многосеточным методом (Full MultiGrid).
В данной работе используется именно полный многосеточный метод, так как он требует O(n) – в отличие от O(nlogn) для V- и W- циклов - операций для достижения требуемой точности, а значит асимптотически лучше, чем методы, состоящие из V- и W- циклов [19].
Реализация этапа проекции
Входные данные
Как уже было сказано ранее, солвер для вычисления давления решает задачу численно эквивалентную решению уравнения Пуассона, однако внутри расчётной области могут быть произвольным образом разбросаны узлы, содержащие граничные условия: как Дирихле, так и Неймана.
Большая часть условий Дирихле равна нулю, т.к. обозначает те области пространства, в которых нет дыма. В том случае, если в поставленной задаче есть ненулевые условия Дирихле, они упаковываются в формат CSR и передаются в солвер.
С условиями Неймана все немного сложнее. У каждой ячейки MACgrid’а 6 нормалей, а значит, при подобном подходе нам придётся передавать в солвер 6 CSR-векторов с граничными условиями Неймана, а затем распаковывать их на GPU. В процессе вычисления так же придётся где-то хранить узлы «призраки», возникающие в результате расчёта условий Неймана.
Гораздо проще подставить формулы аппроксимации для «узлов-призраков» в изначальную систему разностных уравнений. В этом случае сами «узлы-призраки» будут вычеркнуты из системы, а значения граничных условий перейдут в  .
.
Это можно выполнить следующим образом (см выкладки в [17]):
Предположим, что ячейка с индексом (i+1,j,k) заполнена твердым телом, тогда задано условие Неймана:


Подставим  в исходное разностное уравнение. Получаем:
в исходное разностное уравнение. Получаем:

Заметим, что коэффициент при  изменился, и он равен количеству невыколотых соседей
изменился, и он равен количеству невыколотых соседей  . Запомним это - с коэффициентом мы будем работать на этапах сглаживания и подсчёта невязки. Так же заметим, что заданное значение условия Неймана вычитается из правой части. Это вычитание можно произвести уже сейчас на этапе подготовки входных массивов, что и выполняется.
. Запомним это - с коэффициентом мы будем работать на этапах сглаживания и подсчёта невязки. Так же заметим, что заданное значение условия Неймана вычитается из правой части. Это вычитание можно произвести уже сейчас на этапе подготовки входных массивов, что и выполняется.
Итого солвер получает на вход: маску, хранящую информацию о том, находится ли в данной точке дым, воздух или твердый объект, CSR сетку с ненулевыми значениями условий Дирихле и правую часть уравнения, исправленную в соответствии с заданными условиями Неймана.
Сглаживатель
Первый этап работы многосеточного решателя – это сглаживание. В качестве сглаживателя разумно использовать схему «красное-черное» для метода Гаусса-Зейделя, позволяющую добиться эффективного распараллеливания на GPU[16].
Узлы с чётной суммой координат помещаются в одну «красную» группу, а узлы с нечётной суммой в другую «чёрную». Затем для каждой из групп поочередно выполняются итерации метода Якоби. Такое разбиение помогает CUDA-потокам при распараллеливании на GPU на каждом шаге либо только читать, либо только писать в узел, что делает вычисления детерминированными и значительно ускоряет производительность.
Таким образом, принимая во внимание главу о граничных условиях, нам необходимо выполнить:

Где верхние индексы обозначают итерацию,  – значение правой части дополненное граничными условиями Неймана, а
– значение правой части дополненное граничными условиями Неймана, а 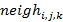 – количество соседних невыколотых узлов, причем
– количество соседних невыколотых узлов, причем  , если (i,j,k) узел выколот.
, если (i,j,k) узел выколот.
Как уже было сказано, метод «красное-чёрное» позволяет добиться хорошего качества распараллеливания на GPU. Так как каждый из узлов одного цвета при выполнении итераций сглаживания зависит только от узлов другого цвета, внутри итерации для каждого из узлов выполняется либо чтение, либо запись, но никогда не обе операции. Данный подход позволяет достичь скорости метода Гаусса-Зейделя, использовав для расчетов на каждой итерации только одну сетку, а не две, как в случае с методом Якоби[22].

Рисунок 3: Красно-чёрная раскраска сетки. Срез на одном из слоев расчетной сетки. При расчёте черных узлов используются значения из красных и наоборот.
Однако у данного подхода есть несовершенство при использовании на графических ускорителях – шаблон доступа к памяти. Графические ускорители устроены таким образом, что наибольшая производительность достигается, когда все потоки работают с участками памяти, расположенными подряд[21]. По этой причине в данной реализации каждый расчётный слой хранится в линеаризованном массиве таком, что в нем сначала расположены только «красные» узлы, а затем только «чёрные». CUDA-ядра при этом работают на CUDA-grid’ах, вытянутых в линию. Таким образом на каждой итерации CUDA-ядра читают данные только из одного массива, а пишут в другой. Для того, чтобы не возникало путаницы, индекс в линеаризованном массиве рассчитывается специальной функцией по координатам узла, и такой подход используется для всех сеток внутри солвера, включая невязки, маски и правые части.
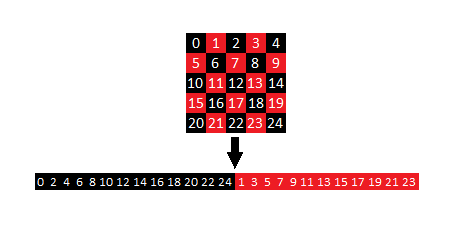
Рисунок 4: Линеаризация двумерного массива
Расчёт невязки
Расчёт невязки является операцией по реализации очень похожей на операцию сглаживания, поэтому работа с граничными условиями характерная для сглаживания характерна и для нее.
Невязка рассчитывается по формуле:
 , т.е.
, т.е. 
Где количество соседей, считается так же, как в сглаживателе. Сокращение слагаемых происходит тем же образом.
Расчёт нормы невязки
Чтобы уменьшить время расчёта, выполнение критерия останова проверялось не после V-цикла, а после выполнения итераций предварительного сглаживания на самой точной сетке. Такой подход, во-первых, позволяет сэкономить на расчёте невязки, так как в случае невыполнения критерия останова её все равно пришлось бы считать, а, во-вторых, на времени выполнения V-цикла. Так как операции предварительного сглаживания на точной сетке производятся гораздо быстрее, чем весь V-цикл, если критерий останова достигается за счет сглаживания до начала огрубления, то нет необходимости выполнять последующие вычисления.
В качестве метрики для проверки критерия останова использовалась норма Гёльдера: 
Особенностью реализации подсчёта нормы на GPU является редукция переменных из warp’ов, которые, вообще говоря, могут не выполняться одновременно.
Был использован алгоритм, заключающийся в следующей последовательности действий:
1. Редукция внутри одного thread’а.
2. Редукция внутри одного warp’а.
3. Редукция внутри одного CUDA-блока.
4. Редукция внутри всего CUDA-grid’а.
Начиная с архитектуры Kepler, для видеокарт NVidia стало возможным получение в CUDA-потоке данных, лежащих в регистрах соседних CUDA-потоков. Так как доступ к файлу регистров такой же быстрый, как доступ к L1-кэшу, данный подход в комбинации с методом сдваивания является наилучшим для редукции внутри одного warp’a.
 |
На языке CUDA его можно описать так:
Данный подход не применим внутри всего CUDA-блока, т.к. чтение из соседних регистров возможно только внутри warp’a.
Для вычислений внутри блока в CUDA есть еще один тип памяти, работа с которой по производительности эквивалентна работе с L1 кэшем – shared (разделяемая память). Доступ к общей для нескольких thread’ов shared памяти возможен только внутри одного CUDA-блока, поэтому с ее использованием мы не можем произвести редукцию по всему grid’у, но можем выполнить ее внутри одного CUDA-block’a следующим образом:
1. Выделяем внутри для каждого блока массив в shared-памяти, вмещающий по одному числу с плавающей запятой, для каждого warp’a. Внутри одного блока может быть не более 1024 потоков – значит для того, чтобы вместить информацию из всех warp’ов достаточно 1024/32 =32 ячеек массива.
2. Нулевой поток каждого warp’а записывает результат внутренней редукции warp’а в отведенную для него ячейку.
3. Происходит синхронизация потоков.
4. Нулевой warp блока осуществляет редукцию указанного массива с помощью приведенного ранее алгоритма.
 Теперь осталось произвести поблочную редукцию внутри grid’а. Здесь придётся воспользоваться глобальной памятью. В CUDA нет атомарной операции выбора максимального из двух чисел с плавающей запятой, но её можно реализовать с помощью атомарной операции сравнения и замены целых чисел, представив число с плавающей запятой, как целое:
Теперь осталось произвести поблочную редукцию внутри grid’а. Здесь придётся воспользоваться глобальной памятью. В CUDA нет атомарной операции выбора максимального из двух чисел с плавающей запятой, но её можно реализовать с помощью атомарной операции сравнения и замены целых чисел, представив число с плавающей запятой, как целое:
8.5 Операторы огрубления и пролонгации
В данной работе используются полновзвешенный (full-weighted) 27-точечный оператор огрубления с билинейной интерполяцией (см Рисунок 4.). Для пролонгации на более точные сетки так же используется оператор билинейной интерполяции (см Рисунок 5). При этом, если узел, в который происходит пролонгация не является рабочим, т.е. является узлом заполненным воздухом или твердым телом, никакие данные в него не записываются, его значение остаётся равным нулю.

Рисунок 5: Веса узлов в операторе огрубления.
Стоит отметить, что, если такой узел находится в зоне огрубления, то при замене значения этого узла на ноль, как например сделано в работе [23], оператор огрубления будет терять часть данных за счёт использования значения того узла, который не будет обновлен при пролонгации. Поэтому в данной работе оператор огрубления был модифицирован – знаменатели дробей, обозначающих вес того или иного узла, при огрублении рассчитываются динамически по следующему алгоритму:
1. Числители всех весов выставляются равными нулю. Общий знаменатель всех дробей выставляется равным нулю.
2. Если огрубляемый узел является рабочим, то его числитель приравнивается к единице, деленой на значение коэффициента пролонгации для данного узла, а общий делитель увеличивается на это значение.
3. Шаг 2 выполняется для всех точек огрубляемой области.
Такой оператор хорош тем, что не меняет сумму всех узлов при последовательном огрублении и пролонгации.
При пролонгации грубого решения на более точную сетку можно заметить, что сама по себе уточненная сетка не используется нигде, кроме сложения ее с приближенным решением на точной сетке. Объединения процессов пролонгации и сложения позволяет сэкономить память на хранении промежуточных данных, а также увеличить производительность за счет использования компилятором инструкций, производящей умножение и сложение за один такт.
Следует обратить внимание на то, что в каждый узел запись производится сразу несколькими потоками. Операция сложения в CUDA по умолчанию не является атомарной, а атомарная выполняется пропорционально количеству одновременных вызовов. Данную проблему можно обойти правильной последовательностью выполнения сложений – например, сначала сложить все узлы, находящиеся в верхних половинах пролонгируемых областей, затем в левых, затем произвести синхронизацию потоков и выполнить сложения для правых, а затем и нижних частей.
Кроме того, можно заметить, что часть узлов будет обновлено сглаживателем сразу же после пролонгации, а их значения не будут использованы. В данном случае это будут все узлы, помеченные для сглаживателя, как «красные» (см Рисунок 5), соответственно для увеличения производительности при пролонгации, вообще, не следует обновлять эти узлы.

Рисунок 6: Коэффициенты оператора пролонгации. Цветами отмечена "раскраска" узлов точной сетки.
Типы ячеек при огрублении определяются следующим образом:
1. Если хотя бы один узел в зоне огрубления содержит граничное условия Дирихле (ячейка заполнена воздухом либо задаёт константный поток газа на границе), то полученный узел считается так же имеющим условие Дирихле.
2. В противном случае, если в зоне огрубления есть хотя бы один рабочий узел (узел с газом), то полученный узел так же считается рабочим.
3. В остальных случаях узел считается выколотым (твердое тело).
Такой подход хорош тем, что на грубых сетках процент выколотых областей будет уменьшаться, а расчётных – увеличиваться (см. Рисунок 6). Это позволяет производить вычисления вплоть до самого грубого уровня.
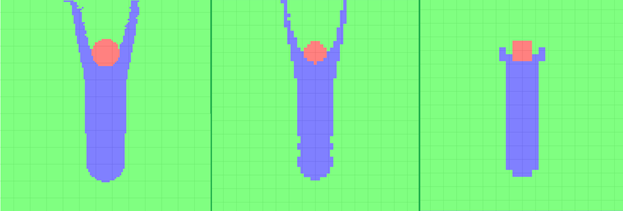
Рисунок 7: Внешний вид маски расчётной области на сетках 129*129*129, 65*65*65 и 33*33*33 соответственно. Синим обозначены рабочие узлы, зеленым узлы с нулевыми граничными условиями Дирихле, красным - твердый объект с условиями Неймана на границе.